Главная » Бесплатные рефераты » Бесплатные рефераты по теории инвестиций »
Задачи с решением по теории инвестиций (дополнения к курсовой работе)
Тема: Задачи с решением по теории инвестиций (дополнения к курсовой работе)
Раздел: Бесплатные рефераты по теории инвестиций
Тип: Задача | Размер: 345.61K | Скачано: 897 | Добавлен 04.02.10 в 13:46 | Рейтинг: +7 | Еще Задачи
Дополнения к курсовой работе по предмету «Теория инвестиций» на тему «Модели оценки опционов, их роль в инвестиционном анализе».
Расчетная часть.
Задача 3.
Имеется следующая информация о сроках обращения и текущих котировках бескупонных облигаций.
|
Вид облигации |
Срок обращения (год) |
Рыночная цена |
|
А |
1 |
98,04 |
|
В |
2 |
93,35 |
|
С |
3 |
86,38 |
|
Д |
4 |
79,21 |
А) На основании исходных данных постройте график кривой доходности на 4 года.
В) Дайте объяснение форме наклона кривой.
С) Определите справедливую стоимость ОФЗ-ПД со сроком обращения 4 года и ставкой купона 7% годовых, выплачиваемых один раз в год.
Решение.
А) На основании исходных данных постройте график кривой доходности на 4 года.
Доходность к погашению бескупонной облигации можно определить по следующей формуле:
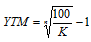
Где K – курсовая стоимость (рыночная цена), n – период обращения
Для каждого вида бумаг получим:
|
Вид облигации |
Срок обращения (год) |
Рыночная цена |
Доходность |
|
А |
1 |
98,04 |
0,020 |
|
В |
2 |
93,35 |
0,035 |
|
С |
3 |
86,38 |
0,050 |
|
Д |
4 |
79,21 |
0,060 |
Построим график зависимости доходности от рыночной цены:
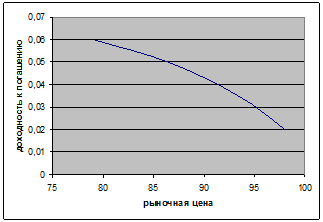
Рис.1. График зависимости доходности от рыночной цены.
В) Дайте объяснение форме наклона кривой.
Облигации с более высокой рыночной ценой имеют меньшую доходность, то есть зависимость между рыночной ценой и доходностью обратная и форма наклона кривой имеет вид, показанный на рис. 1.
Это объяснятся тем, что цена облигации растет по мере приближения срока ее погашения, а так как доходность бескупонной облигации определяется в основном отношением ее рыночной цены к номиналу, то чем дольше остается до погашения облигации (чем больше срок его обращения), тем больше разница между ее ценой и номиналом и тем выше доходность облигации.
С) Определите справедливую стоимость ОФЗ-ПД со сроком обращения 4 года и ставкой купона 7% годовых, выплачиваемых один раз в год.
По бескупонной облигации осуществляется только один платеж – в конце периода ее обращения инвестору выплачивается номинал. Поэтому ее цена определяется по формуле:
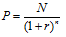
Согласно формуле справедливая цена облигации равна
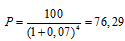
Ответ: справедливая стоимость ОФЗ-ПД будет составлять 76,29.
Задача 10.
Ниже приведена информация о ценах акций «А» и «В» за несколько лет.
|
Год |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
А |
7,07 |
9,29 |
23,20 |
53,56 |
38,25 |
18,11 |
13,10 |
24,23 |
19,32 |
17,12 |
|
В |
0,71 |
4,33 |
29,62 |
108,17 |
15,03 |
8,87 |
8,18 |
22,51 |
37,68 |
39,18 |
А) Определите среднюю доходность и риск акций за рассматриваемый период.
В) Предположим, что инвестор формирует портфель из данных акций в пропорции 50% на 50%. Определите доходность и риск такого портфеля.
С) Постройте график эффективной границы Марковица при условии, что акции «А» и «В» являются единственными объектами, доступными для инвестирования.
Решение.
А) Определите среднюю доходность и риск акций за рассматриваемый период.
Доходность акций определим из соотношения цены продажи и цены покупки, принимая каждое следующее значение за цену продажи, каждое предыдущее за цену покупки. Тогда доходность акций будет определяться для каждого периода как:
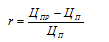
Получим следующие значения доходности акций:
|
Год |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
А |
0,31 |
1,50 |
1,31 |
-0,29 |
-0,53 |
-0,28 |
0,85 |
-0,20 |
-0,11 |
|
В |
5,10 |
5,84 |
2,65 |
-0,86 |
-0,41 |
-0,08 |
1,75 |
0,67 |
0,04 |
Средняя доходность актива определяется как средняя арифметическая доходностей актива за наблюдаемые периоды, а именно:
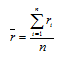
Средняя доходность акций «А» составит
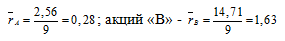
Риск оценим величиной среднеквадратического отклонения доходности акций в каждый из периодов от значения средней доходности актива:
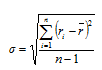
Получим значения величин риска каждой акции:
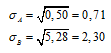
В) Предположим, что инвестор формирует портфель из данных акций в пропорции 50% на 50%. Определите доходность и риск такого портфеля.
Доходность портфеля определим из формулы (-удельный вес каждого актива в портфеле):
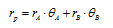
Доходность портфеля будет равна
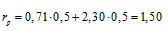
Риск портфеля определяется по формуле:
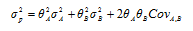
Ковариация доходности активов А и В определяется по формуле:
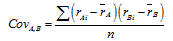
Этот показатель определяет степень взаимосвязи и направление изменения доходностей активов.
Для расчета показателя ковариации определим:
- отклонения доходностей акций от их среднего значения
|
А |
0,03 |
1,21 |
1,02 |
-0,57 |
-0,81 |
-0,56 |
0,56 |
-0,49 |
-0,40 |
|
В |
3,46 |
4,21 |
1,02 |
-2,50 |
-2,04 |
-1,71 |
0,12 |
-0,96 |
-1,59 |
- произведения отклонений для каждого периода и просуммируем их:
|
|
0,10 |
5,10 |
1,04 |
1,42 |
1,66 |
0,96 |
0,07 |
0,47 |
0,64 |
В сумме получаем 11,46
Определяем значение ковариации, разделив полученную сумму на число временных периодов n:
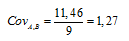
Риск портфеля будет равен:
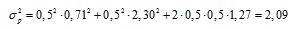
С) Постройте график эффективной границы Марковица при условии, что акции «А» и «В» являются единственными объектами, доступными для инвестирования.
Если объединить в портфель некоторое число активов, корреляция доходности которых лежит в диапазоне от -1 до +1, то, в зависимости от их удельных весов, можно построить множество портфелей с различными параметрами риска и доходности, которые расположены в рамках фигуры ABCDE, как показано на рис. 2.
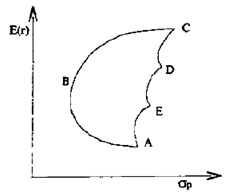
Рис.2. График эффективной границы Марковица.
Рациональный инвестор будет стремиться минимизировать свой риск и увеличить доходность. Поэтому всем возможным портфелям, представленным на рис.2, вкладчик предпочтет только те, которые расположены на отрезке ВС, поскольку они являются доминирующими по отношению к портфелям с тем же уровнем риска или с той же доходностью. Набор портфелей на отрезке ВС называют эффективным набором.
Эффективный набор портфелей – это набор, состоящий из доминирующих портфелей. Набор портфелей на участке ВС называют еще эффективной границей. Она открыта Г.Марковицем в 50-х гг. Чтобы определить данную границу, необходимо рассчитать соответствующие удельные веса, входящих в портфель активов, при которых минимизируется значение стандартного отклонения для каждого данного уровня доходности, т. е. решить уравнение:
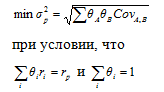
Составим в MS Excel динамическую таблицу, в которой будет производиться расчет минимального риска портфеля при каждом заданном соотношении долей каждого актива в портфеле:

Далее, подставляя различные значения в поле «Доходность портфеля» с помощью инструмента «Поиск решения» определяем различные соотношения бумаг в портфеле и соответствующий уровень риска портфеля:
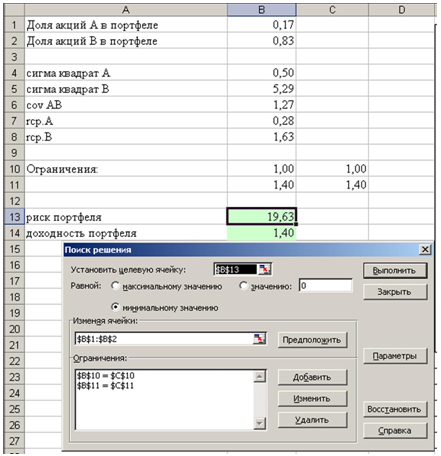
Получим следующие значения:
|
Доходность |
Риск |
Доля акций А в портфеле |
Доля акций В в портфеле |
|
0,28 |
0,25 |
1,00 |
0,00 |
|
0,35 |
0,43 |
0,95 |
0,05 |
|
0,50 |
1,27 |
0,84 |
0,16 |
|
0,70 |
3,37 |
0,69 |
0,31 |
|
1,00 |
8,65 |
0,47 |
0,53 |
|
1,20 |
13,57 |
0,32 |
0,68 |
|
1,40 |
19,63 |
0,17 |
0,83 |
|
1,50 |
23,08 |
0,10 |
0,90 |
|
1,60 |
26,81 |
0,02 |
0,98 |
Эффективная граница Марковица для портфеля из акций А и В графически примет вид:
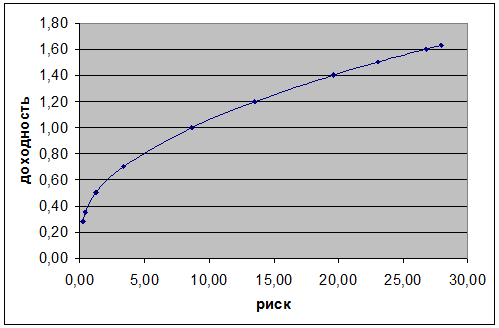
Рис.3. График эффективной границы Марковица для портфеля из акций А и В.
Ответ: за рассматриваемый период средняя доходность акций А составит 28%; акций В – 163%, риск акции А составит 0,71, акции В – 2,3;
также при условии, что портфель из данных акций сформирован в пропорции 50% на 50%, его доходность будет составлять 150%, а риск – 2,09.
Задача 11.
Имеются следующие данные о риске и доходности акций «А», «В» и «С».
|
Акция |
Доходность |
Риск (si) |
Ковариация |
|
А |
0,08 |
0,3 |
σ12 = -0,15 |
|
В |
0,14 |
0,45 |
σ13 = 0,1 |
|
С |
0,26 |
0,6 |
σ23 = 0,3 |
Сформируйте оптимальный портфель при условии, что доходность портфеля должна составлять 12%.
Решение.
Риск портфеля σ вычисляем по формуле:
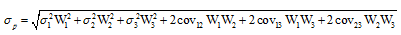
Доходность портфеля:
R=∑WiRi=Wa*0,08+Wb*0,14+Wc*0,26
Целевая функция – риск портфеля → min
Вводим следующие ограничения:
Wa+Wb+Wc=1
0<W<1
R≤0,12
Расчет задачи осуществим в среде MS EXEL. Для решения используем функцию «Поиск решения»:
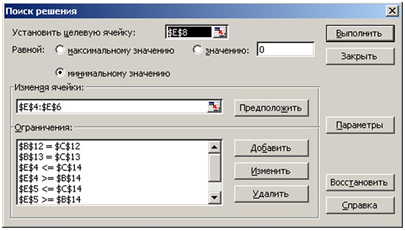
Соответственно предварительно вводим данные задачи в ячейки MS EXEL. Затем задаем необходимые ячейки формулами:
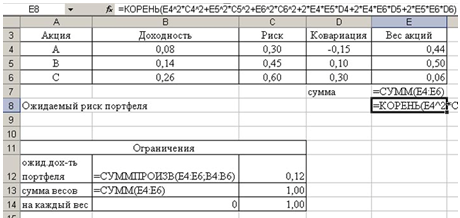
Получаем следующее решение задачи:
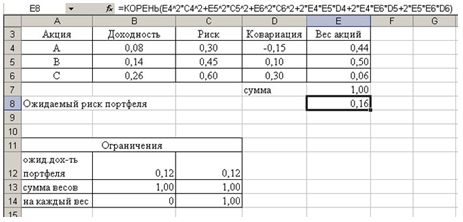
В результате произведенных вычислений имеем:
sп=0,16=16%
W1=0,44=44%
W2=0,50=50%
W3=0,06=6%
Ответ: оптимальный портфель в нашем случае должен состоять на 44% из акций В, на 50% из акций В и на 6% из акций С.
Задача 19.
ОАО «Венера» и «Сатурн» имеют следующие возможности для привлечения заемных средств в сумме 100 млн.
|
Предприятие |
Фиксированная ставка |
Плавающая ставка |
|
«Венера» |
12,0% |
LIBOR + 0,1 |
|
«Сатурн» |
13,4% |
LIBOR + 0,6 |
При этом ОАО «Венера» предпочитает заем по плавающей ставке, а ОАО «Сатурн» - по фиксированной.
А) Разработайте своп, который принесет выгоду обоим предприятиям.
В) Какова максимальная ставка комиссии, которую предприятия могут предложить организатору свопа?
Решение.
А) Разработайте своп, который принесет выгоду обоим предприятиям.
Рассчитаем дельту между ставками:
|
Предприятие |
Фиксированная ставка |
Плавающая ставка |
Разность между дельтами фиксированных и пла- вающих ставок |
|
«Венера» |
12,0% |
LIBOR + 0,1 |
|
|
«Сатурн» |
13,4% |
LIBOR + 0,6 |
|
|
Дельта |
1,4% |
0,5% |
0,9% |
Половину разницы (0,9/2 = 0,45) предприятие «Сатурн» выплачивает «Венере» 13,4% - 0,45% = 12,95%.
«Венера» же выплачивает «Сатурну» плавающую ставку Libor.
Таким образом, платежи и поступления каждого предприятия будут следующими:
Предприятие «Венера»:
- берет заём под 12%
- платит ставку LIBOR предприятию «Сатурн»
- получает от «Сатурна» ставку 12,95%
в итоге получает заем по плавающей ставке LIBOR – 0,95
Предприятие «Сатурн»:
- берет заем по ставке LIBOR + 0,6
- выплачивает «Венере» ставку 12,95%
- получает от «Венеры» LIBOR
в итоге получает заем по фиксированной ставке 12,95 – 0,6 = 12,35%
Таким образом, выигрыш предприятия «Венера» составил 0,1 + 0,95 =1,05%, выигрыш «Сатурна» также составит 1,05% (13,4 – 12,35).
В) Какова максимальная ставка комиссии, которую предприятия могут предложить организатору свопа?
Максимальная ставка комиссии не может быть больше разности между дельтами фиксированных и плавающих ставок, то есть не более 0,9%, что составляет 0,9%*100 млн. = 900 тыс.
Ответ: максимальная ставка комиссии организатору свопа будет составлять 0,9%.
Задача 19.
ОАО «Венера» и «Сатурн» имеют следующие возможности для привлечения заемных средств в сумме 100 млн.
|
Предприятие |
Фиксированная ставка |
Плавающая ставка |
|
«Венера» |
12,0% |
LIBOR + 0,1 |
|
«Сатурн» |
13,4% |
LIBOR + 0,6 |
При этом ОАО «Венера» предпочитает заем по плавающей ставке, а ОАО «Сатурн» - по фиксированной.
А) Разработайте своп, который принесет выгоду обоим предприятиям.
В) Какова максимальная ставка комиссии, которую предприятия могут предложить организатору свопа?
Решение.
А) Разработайте своп, который принесет выгоду обоим предприятиям.
Рассчитаем дельту между ставками:
|
Предприятие |
Фиксированная ставка |
Плавающая ставка |
Разность между дельтами фиксированных и пла- вающих ставок |
|
«Венера» |
12,0% |
LIBOR + 0,1 |
|
|
«Сатурн» |
13,4% |
LIBOR + 0,6 |
|
|
Дельта |
1,4% |
0,5% |
0,9% |
Половину разницы (0,9/2 = 0,45) предприятие «Сатурн» выплачивает «Венере» 13,4% - 0,45% = 12,95%.
«Венера» же выплачивает «Сатурну» плавающую ставку Libor.
Таким образом, платежи и поступления каждого предприятия будут следующими:
Предприятие «Венера»:
- берет заём под 12%
- платит ставку LIBOR предприятию «Сатурн»
- получает от «Сатурна» ставку 12,95%
в итоге получает заем по плавающей ставке LIBOR – 0,95
Предприятие «Сатурн»:
- берет заем по ставке LIBOR + 0,6
- выплачивает «Венере» ставку 12,95%
- получает от «Венеры» LIBOR
в итоге получает заем по фиксированной ставке 12,95 – 0,6 = 12,35%
Таким образом, выигрыш предприятия «Венера» составил 0,1 + 0,95 =1,05%, выигрыш «Сатурна» также составит 1,05% (13,4 – 12,35).
В) Какова максимальная ставка комиссии, которую предприятия могут предложить организатору свопа?
Максимальная ставка комиссии не может быть больше разности между дельтами фиксированных и плавающих ставок, то есть не более 0,9%, что составляет 0,9%*100 млн. = 900 тыс.
Ответ: максимальная ставка комиссии организатору свопа будет составлять 0,9%.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Задачи по теории инвестиций с готовым решением
- Решение задачи №18 по теории инвестиций
- Задача №16 и ее решение по Теории инвестиций
- Задача №11 и ее решение по Теории инвестиций
- Решение по задачам по теории инвестиций (задачи 1, 6, 12, 18, 22)
- Расчеты / задачи по теории инвестиций (№5, №9, №13, №20, №24)
- Задачи и их решение по теории инвестиций (№4, №8)
- Задачи и их решение по теории инвестиций (№8 и №17)
- Решенные задачи по Теории инвестиций
- Задачи и их решение по теории инвестиций (№1, №6, №12, №18, №22)
- Задачи по теории инвестиций с готовыми решениями
![Задачи с решением по теории инвестиций (дополнения к курсовой работе) [04.02.10]](/files/works_screen/54/38.png)