Главная » Бесплатные рефераты » Бесплатные рефераты по теории инвестиций »

Задачи и их решение по теории инвестиций (№1, №6, №12, №18, №22)

Тема: Задачи и их решение по теории инвестиций (№1, №6, №12, №18, №22)

Раздел: Бесплатные рефераты по теории инвестиций

Вуз: ВЗФЭИ

Задача №1

Рассматривается возможность приобретения облигаций внутреннего валютного займа Минфина России. Имеются следующие данные. Дата выпуска –14.05.1996г. Дата погашения –14.05.2011г. Купонная ставка –3%. Число выплат –1 раз в год. Средняя курсовая цена –93,7. Требуемая норма доходности –14% годовых.

Произвести анализ эффективности операции на 25 сентября текущего года.

Решение:

I t=c 25.09.2006 до 14.05.2011-4 года 7 месяцев 19 владения =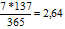

Курсовая цена тогда составит:

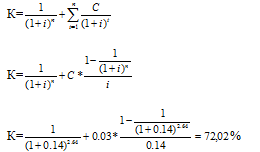
А рыночная курсовая цена составляет 93,7

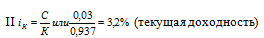
III Эффективность операции будет выше в период владения.

Полная доходность определяется методом интерполяции.

Таким образом получили, что инвестору покупать облигацию невыгодно, поскольку низкая доходность.

Задача №6

Обыкновенные акции предприятия «Ф» продаются по 25,00. В конце периода t=1 ожидаются выплаты дивидендов в размере 2,00. Требуемая инвестором доходность составляет 12%.

а) Определите стоимость акции, если ожидается, что в следующие 3 года дивиденды будут расти на 12 % в год, на 4 и 5 год – на 11 %, а начиная с шестого на 5 %.

б) Изменит ли текущую стоимость акции предположение о её продаже к концу 5 года? Подкрепите выводы соответствующими расчетами.

Решение

P=	25,00	- стоимость акции
DIV=	2,00	- дивидент
g1=	12%	- рост дивидентов 1-3 г.
g2=	11%	- рост дивидентов 4-5 г.
g3=	5%	- рост дивидентов c 6 г.
r=	12%	- доходность

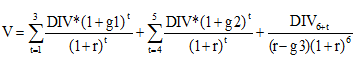
DIV_6+t=DIV*(1+g1)³*(1+g2)²*(1+g3)=3,635124756

T	g	(1+r)^t	*DIV(1+g)^t/ (1+r)^t**	V_6+t
1	0,12	1,12	2
2	0,12	1,25	2
3	0,12	1,40	2
4	0,11	1,57	1,9295224
5	0,11	1,76	1,9122945
6	0,05	1,97		26,309533
			9,8418169
V = 9,8418169 + 26,309533 = 36,1545 – стоимость акции б) V=P+V_1-3+V_4-5= 34,84 – стоимость акции при продаже к концу 5 года. *Ответ:* а) стоимость акции 36,1514; б) стоимость акции при продаже к концу 5-го года составит 34,84.

Задача №12

Рассматривается возможность формирования инвестиционного портфеля из двух акций А и В в равных долях, характеристики которых представлены ниже.

Вид актива	Доходность (в %)	Риск (в %)
А	10,00	30,00
В	25,00	60,00

А) исходя из предположения, что коэффициент корреляции между ними равен 0,25., определите ожидаемую доходность и риск портфеля.

Б) определите оптимальный портфель для требуемой нормы доходности в 20 %

Решение

а) ожидаемая доходность D = 0.1*X₁ + 0.25*X₂, при X₁ = 0.5, X₂ = 0.5 имеем:

D = 0.1*0.5 + 0.25*0.5 = 0.05 + 0.125 = 0.175 или 17.5%.

Задача №12

Вид актива	Доходность (в %)	Риск (в %)
А	10,00	30,00
В	25,00	60,00

Б) определите оптимальный портфель для требуемой нормы доходности в 20 %

Решение

а) ожидаемая доходность D = 0.1*X₁ + 0.25*X₂, при X₁ = 0.5, X₂ = 0.5 имеем:

D = 0.1*0.5 + 0.25*0.5 = 0.05 + 0.125 = 0.175 или 17.5%.

Откуда σ_p = ((0.5)²*((0.3)²+ 2*0.25*0.3*0.6 + (0.6)²))^1/2 = ((0.25*(0.09 + 0.09 +

+ 0.36))^1/2 = (0.25 * 0.54)^1/2 = 0.135^1/2= 0.367 или 36,7 %.

б) имеем систему уравнений: 0.1*X₁ + 0.25*X₂ = 0.2

X₁ + X₂ = 1

из первого и второго: 0.1* X₁+ 0.25*( 1 - X₁) = 0.2 ==>

X₁(0.1 – 0.25) = 0.2 – 0.25 ==> X₁= 1/3 и X₂ = 2/3 – доли акций A и B.

Риск портфеля:

σ_p = 0.3*((1/9) + 4*(4/9) + (2/9))^1/2= 0.1*(1 + 16 + 2)1/2 = 0.1 * 19^1/2= 0.436 или

43.6%.

Ответ: а) ожидаемая доходность 17,5%, риск портфеля 36,7%;

б) оптимальный портфель X₁= 1/3 и X₂ = 2/3 – доли акций A и B, риск портфеля 43,6%.

Задача №18

Текущий курс акции равен 80,00 и может в будущем либо увеличиться до 100,00 с вероятнстью 0,6, либо понизиться до 60,00 с вероятностью 0,4. Цена исполнения опциона «колл» равна 80,00.

Определите ожидаемую стоимость опциона «колл». Определите коэффициент хеджирования и постройте безрисковый портфель.

Решение

Дано: S' = 100 w' = 0.6

S'' = 60 w'' = 0.4

S₀= 80

K = 80

Тогда математическое ожидание цены акции S:

μ = w' S' + w'' S'' = 0.6 * 100 + 0.4 * 60 = 60 + 24 = 84

V' = max(0, S' – K)= 20,

V'' = max (0, S'' – K) = 0.

Ожидаемая цена опциона в момент исполнения:

V = w' V' + w'' V'' = 0.6 * 20 + 0.4 * 0 = 12.

Для безрискового портфеля из δ акций и продажи 1 опциона колл имеем систему уравнений:

δS' - V' = p

δS'' - V'' = p,

где p – цена портфеля. Она одинакова для обоих исходов. Следовательно получаем:

δS' - V' = δS''- V''

откуда: δ*100 – 20 = δ*60 – 0; δ = 0.5.

δ - коэффициент хеджирования - изменение цены опциона при изменении цены базового актива на 1.

Ответ: безрисковый портфель состоит из 0.5 акций и 1 короткого опциона колл.

Цена опциона в момент t=0 равна стоимости безрискового портфеля в момент t=0: δ S'' = δ * 60 = 30.

Задача №22

На рынке капитала конкурируют три банка и паевой фонд, которые предлагают своим клиентам следующие виды финансовых инструментов.

Банк Х продает бескупонные облигации по цене 50,00 с выплатой через год 56,00. Банк Y продает депозитные сертификаты по 2,60 с погашением через год по номиналу 3,00. Банк Z реализует годовые векселя номиналом в 275,00 по цене 250,00.

Паевой фонд Q продает свои паи по 499,99, представляющие собой портфель, в котором содержится 50 депозитных сертификатов банка Y, вексель банка Z и 3 облигации банка Х.

Покажите, что на этом рынке существует возможность арбитража.

Решение

Рассмотрим таблицу:

Наименование	Цена продажи	Номинал/ выплата через год	Доходность
X (бескупонные облигации)	50,00	56,00	12,00%
Y (депозитные сертификаты)	2,60	3,00	15,38%
Z (годовые векселя)	250	275	10,00%
Q (паи)	499,99	-

Рассчитаем стоимость портфеля паевого фонда Q исходя из цен продаж на входящие в него ценные бумаги:

Q = 3Х + 50У + Z = (3*50) + (50*2,60) + 250,00 = 150,00 + 130,00 + 250,00 = 530,00

Q = 530,00 – реальная стоимость пая.

530,00 – 499,99 = 30,01

Ответ: Наличие дизбаланса цен на активы, входящие в портфель паевого фонда Q, показывает, что на данном рынке существует возможность арбитража. Т.е. возможно получение безрискового дохода в пределах суммы равной 30,01. Купив пай ПИФа Q по цене 499,99 и продав его по частям получаем 30,01 прибыли используя арбитраж рынка, которую выгодней всего вложить в депозитные сертификаты банка У, с доходностью 15,38% годовых.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Бесплатная оценка

+41

Размер: 30.14K

Скачано: 636

Скачать бесплатно

06.11.08 в 23:06 Автор:

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

Задачи и их решение по теории инвестиций (№1, №6, №12, №18, №22)

Задача №1

Задача №6

Задача №12

Задача №12

Задача №18

Задача №22

Добавление отзыва к работе

Похожие работы