Контрольная по Методам оптимальных решений Вариант №10

Задание 2.

Фирма производит два широко популярных безалкогольных напитка – «Лимонад» и «Тоник». Фирма может продать всю продукцию, которая будет произведена. Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л «Лимонада» требуется 0,02 час работы оборудования, а для производства 1 л «Тоника» - 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л «Лимонада» и «Тоника» соответственно. Ежедневно в распоряжении Фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,1 ден. ед. за 1 л «Лимонада» и 0,3 ден. ед. за 1 л «Тоника». Сколько продукции каждого вида следует производит ежедневно, если цель фирмы состоит в максимизации ежедневной работы?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Решение:

Составим экономико – математическую модель задачи:

В рамках заданных ограничений фирма должна принять решение о том, какое количество каждого вида напитков следует выпускать. Пусть x1 — число литров Лимонада, производимое за день. Пусть x2 — число литров Тоника, производимое за день.

Цена 1 л «Лимонада» таким образом составляет 0,1 х₁ (ден. ед.), а цена 1 л «Тоника» составляет 0,3 х₂ (ден. ед.). Т.к. нам необходимо максимизировать прибыль, получаем целевую функцию:

max f(х_1,х₂) = 0,1 х₁ + 0,3 х₂. — ежедневный доход, ден. ед. Он максимизируется в рамках ограничений на количество часов работы оборудования и наличие специального ингредиента. Это целевая функция задачи — количественное соотношение, которое подлежит оптимизации.

Ограничения задачи имеют вид:

0,02х₁ + 0,04 х₂  24;

0,01х₁ + 0,04 х₂  16;

х_1,2  0.

Ограничения задачи можно изобразить графически.

Время работы оборудования: 0,02 х1 + 0,04 х2 ≤ 24

Проведем прямую 0,02 х1 + 0,04 х2 = 24 

Простейшим способом нанесения прямой на график является нахождение точек пересечения данной прямой с осями координат х1 и х2. Подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при        х1 = 0, х2 = 600. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1200. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,02 х1 + 0,04 х2 ≤ 24

Специальный ингредиент: 0,01 х1 + 0,04 х2 ≤ 16

Проведем прямую: 0,01 х1 + 0,04 х2 = 16

Таким же образом, подставив х1 = 0 в уравнение и рассчитав значение х1, получим, что при х1 = 0, х2 = 400. Подставив х2= 0 в уравнение и рассчитав значение х1, получим, что при х2 = 0 х1 = 1600. Нанесем эти две точки на график и соединим их прямой. Для определения области, которую следует заштриховать, подставим х1= 0 и х2 = 0 в неравенство: 0,01 х1 + 0,04 х2 ≤ 16

Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений.

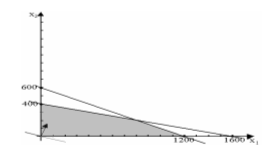
Рис. 1 Область допустимых решений

На Рис. 1 область, отмеченная серым цветом — это допустимое множество, которое содержит все возможные сочетания объемов производства, удовлетворяющие данным ограничениям. Координаты любой точки, принадлежащей допустимому множеству, являются возможным сочетанием объемов производства двух видов напитков, выпускаемых фирмой. Для определения движения к оптимуму построим вектор-градиент. При максимизации функции движемся в направлении вектора-градиента.

Решая систему уравнений

0,02х₁ + 0,04 х₂ = 24;

0,01х₁ + 0,04 х₂ = 16.

Находим, что х₁ = 800, х₂ = 200.

max f(х_1,х₂) = 0,1*800 + 0,3*200 = 140 (ден. ед.)

Проверим правильность расчетов с помощью средств MS Excel:

1. Вводим зависимость для целевой функции и ограничений :

• установим курсор в ячейку D6;

• установить курсор на кнопку «Мастер функций», расположенную на панели инструментов. Щелчком левой кнопки мыши открыть «Мастер функций». На экране появляется диалоговое окно Мастер фун­кций шаг 1 из 2. В окне «Категории» выбираем – Математические, в окне «Функции» выбираем – СУММПРОИЗВ   → «ОК».

На экране появляется диалоговое окно СУММПРОИЗВ;

•  в строку «Массив 1» ввести $B$5:$C$5; адреса ячеек удобнее вводить не с клавиатуры, а протаскивая мышь по указанным ячейкам.

•  в строку «Массив 2» ввести B6:C6;

•  нажать кнопку «ОК».

На экране с помощью функции  СУММПРОИЗВ в ячейку D6 введена функция

Вводим зависимости для ограничений:

•  установить курсор в ячейку D6, нажать правую клавишу мыши – откроется контекстное меню, в нем выбрать - копировать;

•  установить курсор в ячейку E10, нажать правую клавишу мыши – откроется контекстное меню, в нем выбрать – вставить, аналогичные действия и для ячейки E11;(Рис. 2)

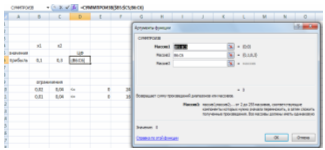
Рис. 2 Введены данные для функции СУММПРОИЗВ и для ЦФ

2. Запустим команду Поиск решения.

На панели инструментов выбрать Данные→ команда Поиск решения → ОК. Появляется диалоговое окно Поиск решения. (Рис.3) Назначим целевую функцию, вводим ограничения и на вкладке Параметры установим Линейная модель и Неотрицательные значения.

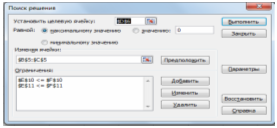
Рис 3. Ввод параметров поиска решений

3. Нажимаем Выполнить. Решение найдено и видим результаты поиска решения.(Рис. 4)

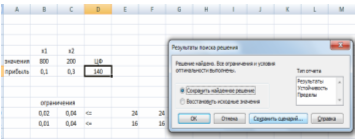
Рис. 4 Результаты поиска решения

Ответ: Максимальная ежедневная прибыль от реализации продукции составит 140 ден.ед. при производстве 800 л "Лимонада" и 200 л "Тоника". Если решать задачу на минимум, то компания прибыли не получит и при производстве продукции понесет убытки.

Задание 3

Машиностроительной компании требуется 250 стартеров СТ-221 в месяц для производства легковых машин. Стоимость заказа 500 руб., стоимость хранения 20 руб. за одну деталь в год. Доставка заказа занимает 3 дня. Компания  работает 300 дней в году. Определите оптимальный объем заказа, период поставок, точку заказа, затраты на управление запасами за год.

Решение:

1.Запускаем программу Excel.

2. Вводим данные в ячейки:

А2 - 300 (дней в год).

С2- объем спроса в год 3000 (250*12).

Е2 - стоимость заказа 500руб.

G2 - стоимость хранения 20руб.

А3 - доставка заказа 3 дня

3. Находим оптимальный размер заказа

В ячейку С4 вводим формулу: =КОРЕНЬ(2*C2*E2/G2) (Рис. 5)

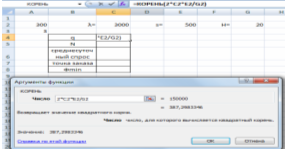
Рис. 5 Оптимальный объем заказа

4. Находим период поставок N.

В ячейку С5 вводим формулу: =C2/C4.

5. Для того чтобы найти точку заказа, сначала находим среднесуточный спрос.

В ячейку С6 вводим формулу: =C2/A2. Далее находим точку заказа.

В ячейку С7 вводим формулу: =A3*C6.

6. Находим минимальные затраты на управление запасами за год.

В ячейку С8 вводим формулу: =КОРЕНЬ(2*C2*E2*G2) (Рис. 6)

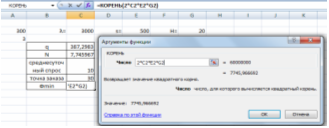
Рис. 6 Минимальные затраты

7. Округляем полученные результаты до целых чисел с помощью Формата ячеек.

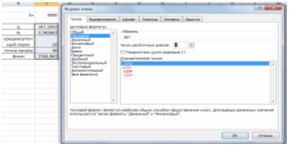
Рис. 7 Округление результатов

8. Решение найдено (Рис. 8)

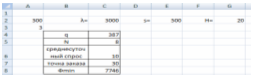
Рис. 8 Общее решение.

Ответ: таким образом, оптимальный объем заказа 300, период поставок 8 дней, точка заказа 30 и минимальные затраты на управление запасами за год составляют 7746 руб.

Задание 4

В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.), когда оба бухгалтера заняты обслуживанием ранее обратившихся работников, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно l - 10; среднее время, которое затрачивает бухгалтер на оформление документа, равно Т_ср мин. - 12.

Оценить основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%?

Решение:

1. Запускаем Excel.

• Вводим в ячейку С4 интенсивность λ = 10, в ячейку К4 – нагрузка α = 2 и в ячейку G4 – интенсивность μ = 5 (10/2=5).
• Строим таблицу, как показана на рис. 9.

Рис. 9 Ввод данных

2. Находим Сумму каналов.

• В ячейку С7 вводим формулу: =1+($K$4^B7)/ФАКТР(B7)
• В ячейку С8 вводим формулу: =C7+($K$4^B8)/ФАКТР(B8) и протягиваем до ячейки С16.(Рис. 10)

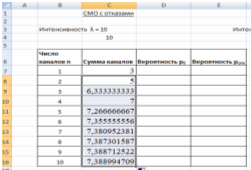
Рис. 10 Сумма каналов

3. Находим вероятность обслуживания р0.
 В ячейку D7 вводим формулу: =C7^-1 и протягиваем до ячейки D16 (Рис. 11).

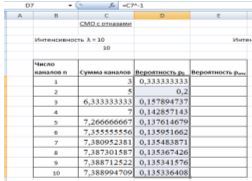
Рис. 11 Вероятность обслуживания

4. Находим вероятность отказа ротк.
В ячейку Е7 вводим формулу: =D7*($K$4^B7)/ФАКТР(B7) и протягиваем до ячейки Е16 (Рис. 12).

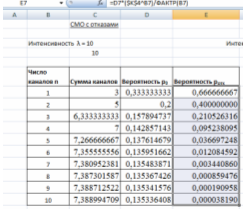
Рис. 12 Вероятность отказа

5. Находим расчет относительной (В) и абсолютной (А) пропускной способности; среднего числа занятых каналов М (п=2). Для начала построим таблицу для ввода данных. (Рис 13).

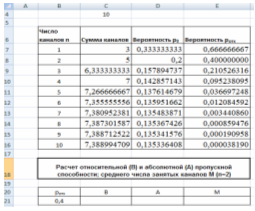
Рис. 13 Ввод данных

• расчет относительной (В) пропускной способности: = 1-B21
• расчет абсолютной (А) пропускной способности: =C4*C21
• среднее число занятых каналов М: =D21/G4

Получим следующую таблицу с результатами (Рис. 14).

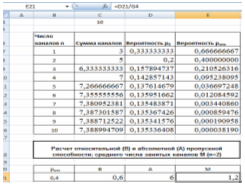
Рис. 14 Расчет относительной и абсолютной пропускной способности и среднего числа занятых каналов

Решение найдено (Рис. 15)

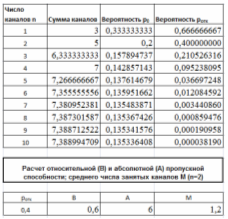
Рис. 15 Расчет характеристик СМО

6. Строим диаграмму вероятности в отказе обслуживания.

• Ставим курсорна кнопку Вставка. Выбираем Диаграммы -  Точечная

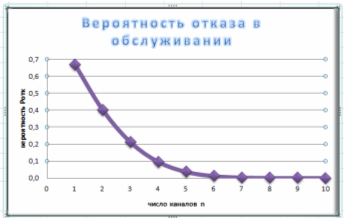
Рис. 16 Точечная диаграмма вероятности отказа в обслуживании

Ответ: Таким образом из диаграммы видно, что минимально число каналов обслуживания (бухгалтеров), при котором вероятность обслуживания работника будет выше 85%, равно n=4.

Задание 5

Статистический анализ показал, что случайная величина Х длительности обслуживания клиента в парикмахерской следует показательному закону распределения с параметром μ = 1,2, а число поступающих в единицу времени клиентов (с.в. У) - закону Пуассона с параметром l = 2,5. Получите средствами MS Excel 15 реализаций с.в. Х и 15 реализаций с.в. У.

Решение:

1. Вводим параметры в ячейку D1 - 2,5, в ячейку F1 – 1,2 и в ячейку С2 число испытаний 15

2. Находим случайные числа с равномерным их распределением в интервале от 0 до 1.

• В ячейку $С$3 вводим формулу: = СЛЧИС() и протягиваем до $Q$3.
• В ячейку С4 вводим формулу: =(-1/$D$1)*LN(C3)
• Кумулятивным образом (строка 6) на временной оси [0,Т] зафиксировано время.
• Для получения время обслуживания в ячейки С7 и С9 записываем формулу: =60*(-1/$F$1)*LN(СЛЧИС())
• Время окончания работы находим по формуле: =C6+C7

3. Далее копируем таблицу и ставим Специальной вставкой. последовательно сравниваем время окончания обслуживания и время поступления требований. Если требование принято к обслуживанию, ставим 0, а если отказано – 1 (Рис. 17).

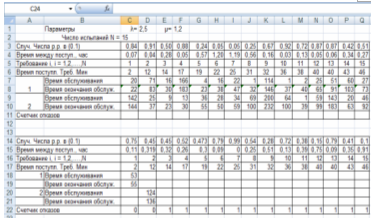
Рис. 17 Статистический анализ

Ответ: в соответствии со счетчиком отказов в ячейках $С$22:$Q$22 зафиксировано 13 отказов, т.е. статистическая оценка вероятности отказа в данной СМО при N = 15 равна (13/15) = 0,87.

Список используемой литературы:

1. Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие, - М.: Вузовский учебник: ИНФРА-М, 2012.
2. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование Учебное пособие. - М.:Вузовский учебник: ИНФРА-М, 2012.
3. Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебное пособие для вузов, - М.: ЮНИТИ, 2001.
4. А.И. Орлов, Теория принятия решений , Учебное пособие. - М.: Издательство "Март", 2004.
5. - КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ, по курсу «УПРАВЛЕНЧЕСКИЕ РЕШЕНИЯ», САНКТ-ПЕТЕРБУРГ 2008 г.