Контрольная по Методам оптимальных решений Вариант 10

Тема: Контрольная по Методам оптимальных решений Вариант 10

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 86.30K | Скачано: 425 | Добавлен 09.06.13 в 21:10 | Рейтинг: +3 | Еще Контрольные работы

Вуз: Финансовый университет

Год и город: Москва 2013

ЗАДАЧА 1

Решить графическим методом типовую задачу оптимизации.

Фирма производит два широко популярных безалкогольных напитка – «Лимонад» и «Тоник». Фирма может продать всю продукцию, которая будет произведена. Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л «Лимонада» требуется 0,02 ч работы оборудования, а для производства 1 л «Тоника» — 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л «Лимонада» и «Тоника» соответственно. Ежедневно и распоряжении фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,10 ден. ед. за 1 л «Лимонада» и 0,30 ден. ед. за 1 л «Тоника». Сколько продукции каждого вида следует производить ежедневно, если цель фирмы состоит в максимизации ежедневной прибыли?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Решение. Данная задача оптимизации является задачей линейного программирования. Сформулируем целевую функцию задачи. Обозначим через переменные х₁ и х₂ количество напитка «Лимонад» и «Тоник» соответственно (в литрах). Целевой функцией задачи является общая выручка от реализации, которая должна быть наибольшей. Число ограничений задачи равно числу ограничений на использование ресурсов — 2. Дополнительно вводится условие неотрицательности переменных. Зная время работы и прибыль фирмы за 1 л., можно сформулировать математическую модель задачи линейного программирования:

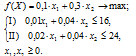
Задачу решаем графическим методом.

Строим область допустимых решений задачи (см. рисунок). Данные для ее построения приведены в таблице:

Ограничение	Граничная прямая	Точки для построения граничной прямой				Неравенство	Выполнение неравенства в контрольной точке (0; 0)
		Точка 1		Точка 2
		x1	x2	x1	x2
I		0	400	1600	0		(да)
II		0	600	1200	0		(да)

Стоим вектор-градиент целевой функции задачи. За его начало принимаем точку (0; 0), тогда концом вектора-градиента будет являться точка с координатами, равными коэффициентам целевой функции по соответствующим координатным осям — (0,1; 0,3). Перпендикулярно вектору-градиенту через точку его начала строится линия нулевого уровня целевой функции — прямая, в каждой точке которой целевая функция принимает нулевое значение: f(X)=0.

Для определения положения точки максимума целевой функции линия, параллельная линии нулевого уровня, смещается в направлении вектора-градиента, до тех пор, пока она не покинет область допустимых решений. Предельная точка области допустимых решений при этом движении и является точкой максимума.

В нашей задаче — это точка B, образованная пересечением граничных прямых ограничений I и II. Ее координаты определяются решением системы уравнений этих прямых:

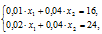
откуда x₁*=800; x₂*=200 и

Таким образом, для получения максимально возможной в данных условиях выручки 140 руб. следует производить 800 л напитка “Лимонад” X₁ и 200 л напитка “Тоник” X₂.

Решение данной задачи линейного программирования на минимум лишено экономического смысла, так как выручку от реализации продукции стремятся получить наибольшей, а не наименьшей. Однако математически эта задача имеет решение и на минимум: наименьшее значение в области допустимых решений целевая функция принимает в точке (0; 0), и это значение равно

ЗАДАЧА 2

Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Вид ресурсов	Нормы расхода ресурсов на ед. продукции			Запасы ресурсов
	I вид	II вид	III вид
Труд	3	6	4	2000
Сырье 1	20	15	20	15000
Сырье 2	10	15	20	7400
Оборудование	0	3	5	1500
Цена изделия	6	10	9

            Требуется:

1. Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
3. Пояснить нулевые значения переменных в оптимальном плане.
4. На основе свойств двойственных оценок и теорем двойственности:
   • проанализировать использование ресурсов в оптимальном плане исходной задачи;
   • определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24 единицы;
   • оценить целесообразность включения в план изделия четвертого вида ценой 11 денежных единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.

Решение. 1. Данная задача оптимизации является задачей линейного программирования. Обозначим количество выпускаемых единиц продукции I, II, III соответственно как х₁, х₂, х₃. Целевой функцией задачи является общая стоимость выпускаемой продукции, которая должна быть наибольшей. Число ограничений задачи равно числу ресурсов, используемых для изготовления изделий — 4. Дополнительно вводится условие неотрицательности переменных. Зная цены изделий, нормы их расхода и запасы ресурсов, формулируем математическую модель исходной задачи линейного программирования:

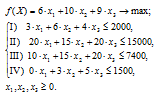
Задачу оптимизации решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL (меню «Сервис»):

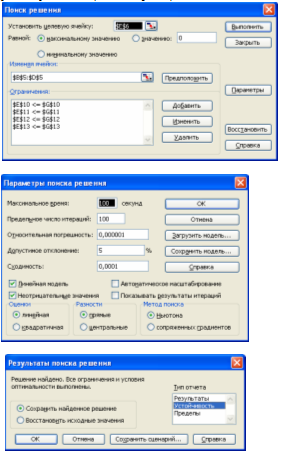
(для копирования снимка окна в буфер обмена данных используется комбинация клавиш Alt + Print Screen).

Использование надстройки позволило получить значения переменных оптимального плана выпуска изделий: Х*=(520; 0; 110). Целевая функция имеет наибольшее для данных условий задачи значение f(X*)=4110 (прил. 1).

Таким образом, для получения наибольшей выручки от реализации продукции следует производить x₁*=520 изделий I, x₃*=110 изделий III и не производить изделия II (x₂*=0).

2. Обозначим двойственные оценки ресурсов I, II, III, IV как y₁, y₂, y₃, y₄ соответственно. Целевой функцией двойственной задачи является общая стоимость запасов ресурсов в двойственных оценках, которая должна быть наименьшей. Число ограничений двойственной задачи равно числу переменных исходной задачи — 3. Математическая модель двойственной задачи имеет вид:

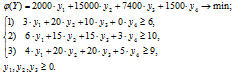
При решении исходной задачи с помощью EXCEL одновременно определяется и оптимальное решение двойственной задачи. В «Отчете по устойчивости» (прил. 2) приводятся теневые цены ресурсов: y₁*=1,5; y₂*=0; y₃*=0,15; y₄*=0.

Наименьшее значение целевой функции двойственной задачи

совпадает (в пределах погрешности округления) с наибольшим значением целевой функции исходной задачи f(X*).

3. Выпуск изделий II невыгоден для данных условий задачи. Это объясняется тем, что стоимость ресурсов на изготовление единицы этой продукции в теневых ценах превышает цену реализации:

4. Проанализируем использование ресурсов в оптимальном плане. Для этого подставим в ограничения исходной задачи значения переменных оптимального плана Х*=(520; 0; 110) и проверим выполнение неравенств:

Видно, что ресурсы I и III используются в оптимальном плане полностью, т. е. являются дефицитными. На это обстоятельство указывает и то, что теневые цены этих ресурсов больше нуля (y₁*>0; y₃*>0). Самым дефицитным является ресурс I, так как он имеет наибольшую теневую цену (y₁*=1,5); наименее дефицитен ресурс  III (y₃*=0,15).

Ограниченные запасы дефицитных ресурсов I и III сдерживают рост объемов выпускаемой продукции и наибольшей выручки от ее реализации. Увеличение объема ресурса I на одну единицу при неизменных объемах других ресурсов ведет к росту наибольшей выручки на 1,5 руб., увеличение объема ресурса III на единицу — на 0,15 руб.        

Ресурсы II и IV являются недефицитными (y₂*=0; y₄*=0), т. е. избыточными в оптимальном плане. Увеличение объемов этих ресурсов не повлияет на оптимальный план выпуска продукции и не увеличит ее общую стоимость.

Определим, насколько изменится общая стоимость выпускаемой продукции при заданных изменениях запасов сырья. Из «Отчета по устойчивости» видно, что эти изменения происходят в пределах устойчивости (см. «Допустимое увеличение» и «Допустимое уменьшение» правых частей ограничений в прил. 2), что дает возможность сразу рассчитать изменение наибольшей выручки от реализации выпускаемой продукции, не решая новую задачу линейного программирования:

При этом «новая» наибольшая выручка составит

 руб.

Для определения целесообразности включения в план выпуска еще и изделия IV с заданными характеристиками рассчитаем стоимость ресурсов на изготовление единицы этого изделия в теневых ценах и сравним это значение с ценой реализации:

Следовательно, продукцию IV выпускать невыгодно, так как она поглощает часть дефицитных ресурсов и тем самым сдерживает рост выпуска выгодной продукции. Это, в свою очередь, препятствует увеличению общей стоимости выпускаемых изделий. Если бы изделие IV реализовывалось по цене равной или большей 15 руб., то его производство было бы выгодным.

ПРИЛОЖЕНИЕ:

         1) рабочий лист EXCEL;

         2) «Отчет по устойчивости».

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Экспертные методы принятия решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10
• Контрольная по Методам оптимальных решений Вариант №10