Главная » Бесплатные рефераты » Бесплатные рефераты по методам оптимальных решений »
Контрольная по Методам оптимальных решений Вариант №10
Тема: Контрольная по Методам оптимальных решений Вариант №10
Раздел: Бесплатные рефераты по методам оптимальных решений
Тип: Контрольная работа | Размер: 343.71K | Скачано: 522 | Добавлен 09.06.13 в 21:18 | Рейтинг: +3 | Еще Контрольные работы
Вуз: Финансовый университет
Год и город: Москва 2013
ЗАДАЧА 1
Задача об оптимальном использовании ограниченных ресурсов
1. Постановка экономической задачи (исходные данные варианта)
Менеджер по ценным бумагам намерен разместить 100 000 ф ст. капитала таким образом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен четырьмя возможными объектами инвестиций А, В, С и D. Объект А позволяет получать 6% годовых, объект В — 8 % годовых, объект С – 10 %, а объект D — 9 % годовых. Для всех четырех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объекты А и В. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект D. Учитывая возможные изменения в политике правительства, предусматривается, что в объект С следует вкладывать не более 20 % инвестиций, тогда как особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала.
Как распорядиться свободными денежными средствами?
2. Экономико-математическая модель задачи
Данная задача является задачей об оптимальном использовании ограниченных ресурсов линейного программирования. Сформулируем целевую функцию задачи. Обозначим через переменные х1 , х2, х3 и х4 суммы, вкладываемые в возможные объекты инвестиций A, B, C и D соответственно.
Сформулируем критерии оптимальности и составим целевую функцию. 0,06х1 - ожидаемая прибыль от объекта инвестиций А, 0,08х2 - ожидаемая прибыль от объекта инвестиций B, 0,1х3 - ожидаемая прибыль от объекта инвестиций С, 0,09 х4 - ожидаемая прибыль от объекта инвестиций D.
Суммарная прибыль от вложения денежных средств в четыре возможных объекта инвестиций А, В, С и D - 0,06х1 + 0,08х2 + 0,1х3 + 0,09 х4 ф. ст., является целевой функцией задачи, которую необходимо максимизировать. Окончательно целевая функция имеет вид:
f(X)= 0,06х1 + 0,08х2 + 0,1х3 + 0,09 х4 → max.
Сформируем систему ограничений на изменение значений переменных х1 , х2, х3 и х4. Имеются пять ограничений по размеру вложения инвестиций в четыре возможных объекта инвестиций А, В, С и D:
- Ограничение по общей сумме вклада имеет вид: х1 + х2+ х3 + х4 = 100 000
- Не менее половины инвестиций необходимо вложить в объекты А и В, следовательно ограничение объема вложенных инвестиций в объекты А и В имеет вид: х1 + х2 ≥ 50 000
- Не менее 25% общей суммы капитала нужно поместить в объект D, следовательно, ограничение объема вложенных инвестиций в объект D имеет вид: х4 ≥ 25 000
- В объект С следует вкладывать не более 20 % инвестиций. Следовательно, ограничение объема вложенных инвестиций в объект С имеет вид: х3 ≤ 20 000
- Особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала. Следовательно, ограничение объема вложенных инвестиций в объект А имеет вид: х1 ≥ 30 000.
Дополнительно на значения переменных накладывается ограничение неотрицательности.
Окончательно математическая модель задачи оптимизации будет иметь вид:
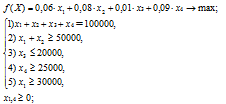
3. Компьютерная технология получения оптимального решения
Данную задачу решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:
-
В ячейках В4:E4 находятся значения переменных х1, х2, х3 и х4 соответственно. Первоначально в них помещаются произвольные числа, например, единицы.
-
В ячейки В5:E5 помещаются коэффициенты при переменных в целевой функции задачи.
-
В ячейку D5 вводится выражение целевой функции с использованием встроенной функции «СУММПРОИЗВ». Аргументами этой функции являются вышеуказанные массивы ячеек B4:E4 и B5:E5. Формула в ячейке D5, таким образом, имеет вид: =СУММПРОИЗВ($B$4:$E$4;B5:E5).
-
В ячейки В10:С14 помещаются коэффициенты при переменных в ограничениях задачи.
-
В ячейки F10:F14 вводятся выражения левых частей ограничений также с использованием функции «СУММПРОИЗВ». Например, в ячейке F10 формула имеет вид: =СУММПРОИЗВ($B$4:$E$4;B10:E10).
-
В ячейках G10:G14 для удобства и наглядности указываются знаки в ограничениях.
-
В ячейки H10:H14 вводятся значения правых частей ограничений.
Исходный рабочий лист EXCEL, таким образом, имеет вид:
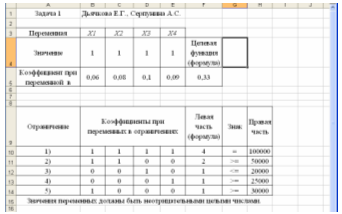
Для решения задачи оптимизации запускается надстройка «Поиск решения» (меню «Сервис») и заполняются все необходимые поля в панели надстройки:
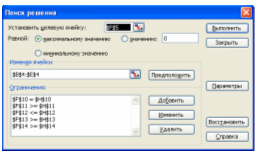
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных:
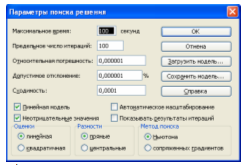
4. Решение задачи
После запуска надстройки «Поиск решения» на выполнение было получено сообщение об успешном решении задачи оптимизации:
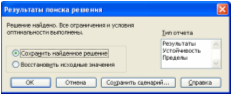
В окне «Тип отчета» выбирается пункт «Результаты».
Рабочий лист EXCEL, содержащий результаты решения, имеет вид:
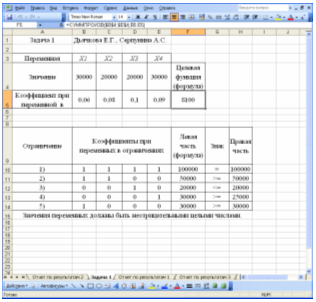
5. Предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению
Таким образом, чтобы получать максимальные годовые проценты с дохода, в объект А необходимо вложить 30000 ф ст., в объект B – 20000, в объект С – 20000 и в объект D – 30000 ф ст.
ПРИЛОЖЕНИЕ:
1) рабочий лист EXCEL;
2) «Отчет по результатам».
ЗАДАЧА 2
Задача о назначениях
1. Постановка экономической задачи (исходные данные варианта)
Фирма получила заказы на выполнение ремонтных работ на пяти объектах (евроремонт пяти квартир). Для выполнения этих заказов фирма располагает шестью бригадами, каждая из этих бригад выполняет один заказ «под ключ». Ниже в таблице приведены оценки времени (в днях), необходимого бригадам для выполнения всех работ и сдачи объектов заказчикам (исходя из состава и квалификации работников бригады).
|
Время выполнения, ч
Работник |
Объект 1
|
Объект 2 |
Объект 3 |
Объект 4 |
Объект 5 |
|
Р1 |
47 |
60 |
25 |
63 |
68 |
|
Р2 |
48 |
57 |
33 |
56 |
71 |
|
Р3 |
45 |
53 |
20 |
62 |
61 |
|
Р4 |
48 |
60 |
18 |
65 |
74 |
|
Р5 |
44 |
66 |
21 |
61 |
76 |
|
Р6 |
42 |
54 |
29 |
55 |
69 |
Оценки даны бригадирами, и опыт работы их в фирме дает основания руководству доверять им.
Распределить объекты работ между бригадами, чтобы общее количество человеко-дней, затраченное на выполнение работ на всех пяти объектах, было минимальным.
2. Экономико-математическая модель задачи
Данная задача является задачей о назначениях и реализуется как частный случай транспортной задачи. Видно, что число бригад (6) превышает количество объектов, на которых должен быть выполнен ремонт (5). Следовательно, задача является открытой, и решать ее целесообразно путем приведения к закрытой задаче, для чего вводится фиктивная операция — Объект 6. Время на выполнение операции на фиктивном объекте равно нулю, так как она фактически не выполняется.
Представим исходные данные закрытой задачи в виде таблицы:
|
Время выполнения, ч
Работник |
Объект 1
|
Объект 2 |
Объект 3 |
Объект 4 |
Объект 5 |
Объект 6 |
|
Р1 |
47 |
60 |
25 |
63 |
68 |
0 |
|
Р2 |
48 |
57 |
33 |
56 |
71 |
0 |
|
Р3 |
45 |
53 |
20 |
62 |
61 |
0 |
|
Р4 |
48 |
60 |
18 |
65 |
74 |
0 |
|
Р5 |
44 |
66 |
21 |
61 |
76 |
0 |
|
Р6 |
42 |
54 |
29 |
55 |
69 |
0 |
Обозначим через xij факт назначения i–ой бригады на выполнение j–го объекта (1 — если бригада назначена, 0 — если не назначена). Математическая модель задачи имеет вид:
Найти такие значения xij, чтобы суммарное время на выполнение всех работ было наименьшим:
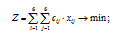
и при этом:
· каждая бригада должна быть назначена только на один объект:
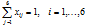
· на каждый объект должна быть назначена только одна бригада:
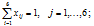
· переменные задачи являются двоичными:
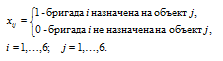
3. Компьютерная технология получения оптимального решения
Данную задачу решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:
-
В ячейки B5:F10 вводятся затраты времени, необходимого рабочим на выполнение операций;
-
В ячейках B14:G19 находятся значения переменных xij. Первоначально в них помещаются произвольные числа, например, единицы.
-
В ячейки H14:H19 вводятся формулы для расчета сумм значений переменных в соответствующих строках. Например, в ячейке H14 формула имеет вид: =СУММ(B14:G14).
-
В ячейки B20:G20 вводятся формулы для расчета сумм значений переменных в соответствующих столбцах. Например, в ячейке B20 формула имеет вид: =СУММ(B14:B19).
-
В ячейку B22 вводится выражение целевой функции задачи с использованием встроенной функции EXCEL «СУММПРОИЗВ». Аргументами этой функции являются блоки ячеек, содержащие затраты времени и значения переменных: =СУММПРОИЗВ(B5:H11;B15:H21).
Лист исходных данных, таким образом, имеет вид:
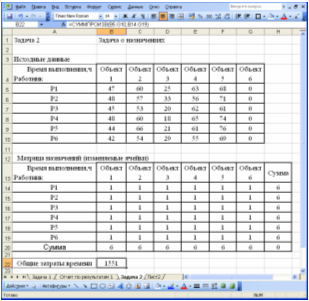
После ввода исходных данных запускается надстройка «Поиск решения» (меню «Сервис» ® «Поиск решения…») и заполняются необходимые поля в панели надстройки:
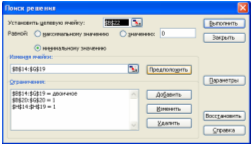
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных:
4. Решение задачи на ЭВМ
После запуска надстройки «Поиск решения» на выполнение было получено сообщение об успешном решении задачи оптимизации:
В окне «Тип отчета» выбираем пункт «Результаты».
Рабочий лист EXCEL, содержащий результаты решения имеет вид:
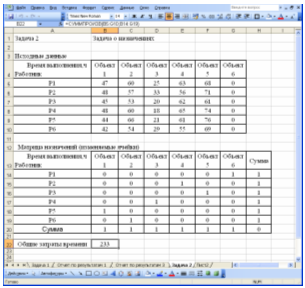
5. Предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению
Таким образом, чтобы общее количество человеко-дней, затраченное на выполнение работ на всех пяти объектах, было минимальным, следует назначить:
- рабочего 2 на объект 4;
- рабочего 3 на объект 5;
- рабочего 4 на объект 3;
- рабочего 5 на объект 1;
- рабочего 6 на объект 2;
Работник 1, назначенный на фиктивный объект 6, фактически не работает.
Суммарное время на выполнение всех операций составит 233 ч.
ПРИЛОЖЕНИЕ:
1) рабочий лист EXCEL;
2) «Отчет по результатам».
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
Похожие работы
- Экспертные методы принятия решений Вариант №10
- Контрольная по Методам оптимальных решений Вариант 10
- Контрольная по Методам оптимальных решений Вариант №10
- Контрольная по Методам оптимальных решений Вариант №10
- Контрольная по Методам оптимальных решений Вариант №10
- Контрольная по Методам оптимальных решений Вариант №10
- Контрольная по Методам оптимальных решений Вариант №10
![Контрольная по Методам оптимальных решений Вариант №10 [09.06.13]](/files/works_screen/1/47/21.png)