Тема: Решение задач на сложные проценты, дисконтирование, аннуитеты и др.

Раздел: Бесплатные рефераты по финансовой математике

Тип: Задача | Размер: 101.13K | Скачано: 759 | Добавлен 14.06.15 в 15:21 | Рейтинг: +1 | Еще Задачи

1 ПРОЦЕНТНЫЕ И УЧЕТНЫЕ СТАВКИ

Задача 9

Ссуда получена 15 марта и должна быть возвращена 5 июля. Раз­мер ссуды - 20 тыс. руб. Простая ставка - 15% годовых. Найти совокупный долг (первоначальная ссуда с процентами) исходя из:

а) английской;

б) французской;

в) германской практик определе­ния процентов.

Решение:

Используем формулу наращения для простых процентов:

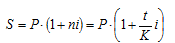
где Р – первоначальная сумма ссуды;

i – ставка простых процентов;

P=20 тыс. руб.

I=0.5

1) точные проценты с точным числом дней ссуды (английская практика):

K=365 (дней) – количество дней в году;

t – количество дней, за которые начисляются проценты;

15 марта – порядковый номер в году – 74;

5 июля – порядковый номер в году – 186.

Точное число дней ссуды:

T=186-74=112  дней.

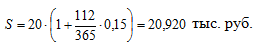
2) обыкновенные проценты с точным числом дней ссуды (французская практика):

K=365  (дней) – количество дней в году;

T=112 (дней) – количество дней, за которые начисляются проценты;

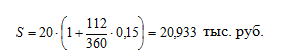
3) обыкновенные проценты с приближенным числом дней ссуды (германская практика):

K=365   (дней) – количество дней в году;

t – количество дней, за которые начисляются проценты;

Рассчитаем приближенное число дней ссуды t. Продолжительность ссуды определяется из условия, согласно которому месяц принимается за 30 дней:

15.03 – 30.03 – 16 дней;

апрель, май, июнь – по 30 дней;

1.07 – 5.07 – 5 дней.

T=16+30*3+5-1=110 дней.

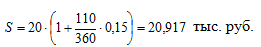
Ответ: совокупный доход за период при начислении процентов по английской практике составит 20920 руб., при использовании французской практики начисления процентов – 20933 руб., а при начислении процентов по германской практике совокупный доход за данный период составит 20917 руб.

 

Задача 19

Рассчитать учетную ставку, которая обеспечивает доход в 6 тыс. руб., если сумма в 10 тыс. руб. выдается в ссуду на полгода.

Решение:

Величина учетной ставки:

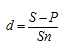
где Р – первоначальная сумма;

S – наращенная сумма;

I=S-P – доход;

n – срок ссуды (лет).

P=10 тыс. руб.

I=6 тыс. руб.

N=0.5 года.

S=10000+6000=16000 руб.

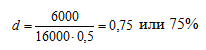
Ответ: учетная ставка в размере 75% обеспечит доход в 6 тыс. руб., если сумма в 10 тыс. руб. выдана в ссуду на полгода.

 

2 СЛОЖНЫЕ ПРОЦЕНТЫ

Задача 9

На сберегательном счете в банке лежат 200 руб. Какая сумма бу­дет находиться на данном счете через три года, если в расчетах используется сложная ставка 12% годовых?

Решение:

Используем формулу наращения для сложных процентов:

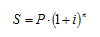
где S – наращенная сумма;

Р – первоначальная сумма долга;

i – ставка сложных процентов;

n – срок ссуды.

P=200 руб.

n=3 года

i=0.12

Наращенная сумма через 3 года составит:

S=200*(1+0.12)3=280.98 руб.

Ответ: на данном счете через три года будет находиться 280,98 рублей.

 

Задача 19

Вексель 300 тыс. долл. учитывается за 2 года до погашения по сложной учетной ставке 10 % годовых. Найти сумму, полученную векселедержателем, и величину дисконта.

Решение:

Полученная при учете векселя сумма определяется по формуле:

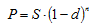
где S – номинальная стоимость векселя;

n – срок от момента учета до даты погашения векселя;

(1-nd) - дисконтный множитель.

S=300 тыс. руб.

n=2 года

d=0.10

P=300*(1-0.1)2=243 тыс. руб.

Размер дисконта определяется по формуле:

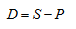
D=300-243=57

Ответ: векселедержатель при учете векселя получит 243 тыс. руб., сумма дисконта составит 57 тыс. рублей.

 

3 МАТЕМАТИЧЕСКОЕ И БАНКОВСКОЕ ДИСКОНТИРОВАНИЕ

Задача 9

Вексель номинальной стоимостью 5 млн. руб. учтен за 15 дней до срока погашения по учетной ставке 18% годовых. Определить дисконт и дисконтированную величину.

Решение:

Полученная при учете векселя сумма определяется по формуле:

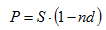
где S – номинальная стоимость векселя;

n – срок от момента учета до даты погашения векселя;

(1-nd) - дисконтный множитель.

S=5 млн. руб.

t=15 дней

K=360 дней

D=0.18

Дисконтируемая величина:

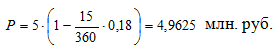
Размер дисконта:

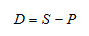
D=5-4.9625=0,0375 млн. руб.

Ответ: Дисконтируемая величина векселя составила 4 962,5 тыс. руб., а величина дисконта 37,5 тыс. руб.

 

Задача 19

Долговое обязательство в сумме 2 млн. руб. должно быть погашено через 90 дней с процентами (12% годовых). Владелец обязательства учел его в банке за 15 дней до наступления срока по учетной ставке 13%. Определить сумму после учета обязательства.

Решение:

Сумма, выплачиваемая при учете обязательства с начислением простых процентов, определяется по формуле:

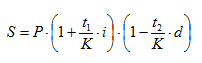
где Р – первоначальная сумма ссуды;

i – ставка простых процентов;

d – простая учетная ставка;

t₁ – общий срок платежного обязательства (срок начисления процентов);

t₂ – срок от момента учета обязательства до даты погашения долга.

P=2 млн. руб.

I=0,12

t1=90

d=0,13

t2=15

K=360 дней

Сумма, полученная при учете, будет равна:

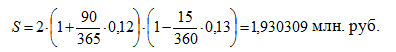
Ответ: При учете долгового обязательства получена сумма в размере 1 930 309 руб.

 

4 ЭФФЕКТИВНАЯ СТАВКА ПРОЦЕНТОВ

Задача 9

Облигация номиналом 10 тыс. руб. выпушена на 3 года при номинальной ставке 6%. Рассчитать эффективную учетную ставку и определить наращенную стоимость по эффективной ставке, если начисление процентов производится один раз в квартал.

Решение:

Эффективная учетная ставка определяется по формуле:

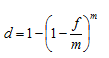
где f – номинальная учетная ставка;

m – число периодов начисления процентов в году.

f=0,06

m=4

Эффективная учетная ставка при ежеквартальном начислении процентов составит:

или 5,87%

Наращенная сумма в случае применения учетной ставки рассчитывается по формуле:

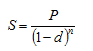
где P – номинальная стоимость облигации;

n – число лет начисления процентов;

d – учетная ставка процентов.

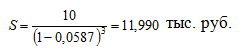
Ответ: эффективная учетная ставка составит 5,87%, а наращенная стоимость облигации будет равна  11 990 рублей.

 

Задача 19

Эффективная ставка при полугодовом начислении процентов составила 18%. Найти годовую номинальную учетную ставку.

Решение:

Эффективная учетная ставка определяется по формуле:

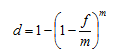
где d – эффективная учетная ставка;

f – номинальная учетная ставка;

m – число периодов начисления процентов в году.

Выразим из формулы номинальную учетную ставку:

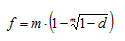
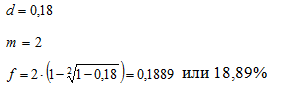
Ответ: годовая номинальная учетная ставка составит 18,89%.

 

5 ЭКВИВАЛЕНТНОСТЬ ПРОЦЕНТНЫХ СТАВОК И СРЕДНИЕ СТАВКИ

Задача 9

Первые два года начисляются сложные проценты по ставке 20%, вторые три года - 30 %, следующий год - 40 %. Найти среднегодовую процентную ставку.

Решение:

В случае сложных процентов среднегодовая процентная ставка определяется по формуле средней гармонической взвешенной:

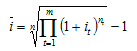
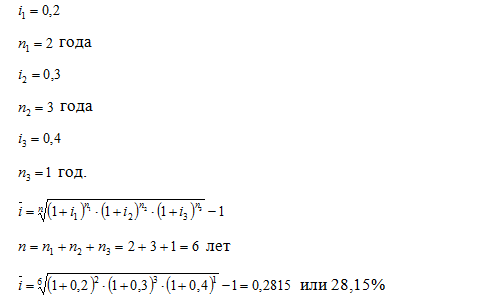
Ответ: среднегодовая процентная ставка за данный период составляет 28,15%.

 

Задача 19

Необходимо найти величину учетной ставки, эквивалентной годовой процентной ставке 40% (К=365) при условии, что срок учета равен 255 дням.

Решение:

Уравнение эквивалентности ставки простых процентов и учетной ставки имеет вид:

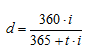
где d – учетная ставка процентов;

i – годовая ставка простых процентов;

t – срок учета.

i=0,40

t=255 дней.

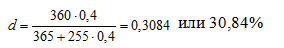
Ответ: годовой процентной ставке 40% эквивалента учетная ставка в размере 30,84%.

 

6 РАСЧЕТ НАРАЩЕННЫХ СУММ В УСЛОВИЯХ ИНФЛЯЦИИ

Задача 9

Кредит 12 тыс. руб. выдан на 3 года. На этот период прогнозируется рост цен в 2,2 раза. Определить ставку процентов при выдаче кредита и наращенную сумму долга, если реальная доходность должна составлять 12% годовых по ставке сложных процентов.

Решение:

Ставка сложных процентов, учитывающая инфляцию, определяется по формуле:

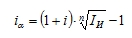
где i_α – процентная ставка, учитывающая инфляцию;

i – реальная ставка процентов;

I_И – темп инфляции за период.

n=3 года

i=0,12

I=2,2

Ставка процентов, учитывающая инфляцию, составит:

или 45,67%.

Наращенная сумма долга в случае сложных процентов:

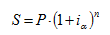
где Р – первоначальная сумма кредита;

i_α – ставка при выдаче кредита (процентная ставка, учитывающая инфляцию);

n – срок кредита.

P=12 тыс. руб.

n=3 года

i=0,4567

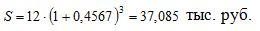
Ответ: ставка процентов при выдаче кредита составит 45,67%, а сумма долга через 3 года будет равна 37 085 рублей.

 

РЕШЕНИЕ ОСТАЛЬНЫХ ЗАДАЧ СМОТРИТЕ В ФАЙЛЕ

 

Задача 19

Найти реальный доход вкладчика, если на депозит положено 25 млн. руб. на 3 года по сложной ставке 20% годовых с ежемесячным начислением процентов при квартальной инфляции, в среднем за данный период равной 3%.

 

7 КОНСОЛИДАЦИЯ ПЛАТЕЖЕЙ

Задача 9

Два платежа 1 и 0,5 млн. руб. со сроками уплаты соответственно 150 и 180 дней объединяются в один со сроком 200 дней. Стороны согласились на применении при конверсии простой ставки, равной 20 %. Определить консолидированную сумму. К=365.

 

Задача 19

В банк положены 300 тыс. руб., на которые ежемесячно начисляются сложные проценты по ставке 24%. Через 4 месяца сняты 5 тыс. руб., а через 8 месяцев вклад был закрыт. Какая сумма была на счете в момент закрытия вклада (решить задачу при помощи дисконтирования)?

 

8 АННУИТЕТЫ (ФИНАНСОВЫЕ РЕНТЫ)

Задача 9

Страховая компания, заключившая договор с производственной фирмой на 3 года, поступающие ежегодные страховые взносы – 5 млн. руб. помещает в банк под 15% годовых с начислением процентов по полугодиям. Определить сумму, полученную страховой компанией по этому контракту.

Задача 19

Замените годовую десятилетнюю ренту с годовым платежом 1000 долл. на ренту с полугодовым платежом по 600 долл. Годовая ставка процентов 8%. n - ?

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Отзывы о работе:

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Решение задач по финансовой математике в Excel
• Сборник задач по финансовой математике с решением
• Задачи по финансовой математике с решением в Excel
• Решение задач по финансовой математике (8 заданий)
• Решенные задачи по финансовой математике с расчетами в Excel
• Решение задач по финансовой математике (9 заданий)