Главная » Бесплатные рефераты » Бесплатные рефераты по логике »
Индуктивные умозаключения
Тема: Индуктивные умозаключения
Раздел: Бесплатные рефераты по логике
Тип: Контрольная работа | Размер: 34.88K | Скачано: 324 | Добавлен 20.05.13 в 17:38 | Рейтинг: 0 | Еще Контрольные работы
План
1. Введение 2
2. Индуктивные умозаключения. Понятие «индуктивное умозаключение». Виды индуктивных умозаключений: полная, неполная индукции 4
3. Условно-категорический силлогизм и его правильные модусы. Утверждающий модус, отрицающий модус. Разделительно-категорический силлогизм. Утверждающе - отрицательный и отрицающее - утверждающий модусы, их правила 7
4. Практическое задание 11
5. Заключение 12
6. Список используемой литературы 13
7. Приложение 1 14
Введение
Большую часть знаний о предметах и явлениях окружающего мира человек получает из уже имеющейся у него информации. При этом он идет по пути выведения нового знания из уже имеющегося. Опосредованно, используя разные виды умозаключений, человек получает новое знание. Поэтому полученное таким путем знание принято называть выводным, или опосредованным. [1, с.49]
Умозаключение – форма мышления. Посредством которой из одного или нескольких суждений выводится с необходимостью или вероятностью новое суждение.
Умозаключение состоит из трех основных компонентов:
1.посылки – исходного суждения, из которого выводят новое знание;
2.вывода – логического перехода от посылок к заключению;
3.заключения – нового суждения, полученного выводным путем из посылок.
По характеру связи между знанием различной степени общности, выраженным в посылках и заключении, различают три вида умозаключений:
1.дедуктивные (переход осуществляется от общего знания к частному знанию);
2.индуктивные (переход от частного знания к общему);
3.умозаключения по аналогии (переход от частного знания к частному знанию) [1, с.50]
Категорический силлогизм — рассуждение мысли, состоящее из трёх простых атрибутивных высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на большую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы.[6]
Цель работы – подробно изучить индуктивные умозаключения и виды, и условно-категорический и разделительно-категорический силлогизмы, их модусы и фигуры.
1.Индуктивные умозаключения. Понятие «индуктивное умозаключение». Виды индуктивных умозаключений: полная, неполная индукции.
Индуктивные умозаключения – это такая форма мышления, посредством которой на основе повторяющегося признака у отдельных явлений делается заключение о его принадлежности всем явлениям данного класса; вывод в индуктивном умозаключении, как правило, носит вероятностный характер. Лишь в полной индукции, когда повторяющийся признак можно выявить у каждого явления данного класса, вывод о принадлежности признака данному классу является необходимым. [1, с.57] Например:
- Железо - твердое тело.
- Медь - твердое тело.
- Золото - твердое тело.
- Железо, медь, золото ... - металлы.
- Все металлы - твердые тела.
Если не исследован весь класс металлов, то достаточно найти хотя бы один элемент данного класса, который не является твердым телом, и весь вывод окажется неистинным. Поскольку мы не можем исследовать все возможные металлы и доказать, что они твердые тела, то заключение в данном выводе является вероятностным суждением.[2]
Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.[3]
В зависимости от полноты исследования предметов какого - либо класса различают полную и неполную индукцию.
Полная индукция - такое умозаключение, в котором общий вывод о классе предметов делается на основании изучения всех предметов данного класса.[2] Очевидно, что при подобном способе умозаключения мы получаем вполне достоверное заключение, которое в то же время в известном отношении расширяет наше познание; этот способ умозаключения не может вызвать никаких сомнений. Отождествив предмет логической группы с предметами частных суждений, мы получим право перенести определение на всю группу.
Схема полной индукции:
Множество А состоит из элементов: А1, А2, А3, …, Аn.
- имеет признак В
- имеет признак В
- Все элементы отА3доАnтакже имеют признакВ
Следовательно, все элементы множества А имеют признак В.[3]
Полная индукция дает достоверные заключения при наличии следующих условий: а) когда класс предметов или явлений, подлежащих изучению, представляет собой небольшое число элементов - ограничен, поддается «регистрации»; б) когда точно известен признак, принадлежащий предметам данного класса.
Разновидностью полной индукции является умозаключение от отдельных частей к целому (от знания успеваемости в каждой группе факультета к общему знанию об успеваемости на всем факультете). Полная индукция может использоваться при расследовании уголовных дел, связанных с исчезновением материальных ценностей (оружия, боеприпасов, продуктов питания и т. д.), число которых можно подсчитать (тем самым выяснить недостающие ценности).
Но чаще всего юристу приходится иметь дело с фактами, количество которых не может быть строго ограничено. Например, с помощью полной индукции нельзя установить достоверность в обобщениях такого рода, как «Счастливые часов не наблюдают», «Все тела тонут», «Гадюки ядовиты» и т. п. В таких обобщениях может использоваться только неполная индукция.[2]
Неполная индукция - такое умозаключение, в котором общий вывод делается на основании изучения некоторой части класса однородных предметов.[2]
Схема неполной индукции:
Множество А состоит из элементов: А1, А2, А3, …, Аn.
- имеет признак В
- имеет признак В
- Все элементы отА3доАkтакже имеют признакB
Следовательно, вероятно, Аk+1 и остальные элементы множества А имеют признак В.[3]
По способу отбора исходного материала и обоснования заключения неполная индукция делится на популярную (через простое перечисление при отсутствии противоречащих случаев) и научную, разновидностями которой являются индукция через отбор или индукция через установление причинной связи.
В популярной индукции факты для посылок берутся без специального методического отбора. Общий вывод о наличии какого-то признака у класса предметов делается на основе наблюдения у некоторых явлений данного класса этого признака и при отсутствии противоречащего случая. В результате этой индукции выводы получаются малоправдоподобными, так как противоречащие случаи могут обнаружиться, и вывод тогда окажется ложным. Например, почти во всех учебниках логики приводится пример с выводом, полученным с помощью неполной индукции, - «Все лебеди белые», который оказался ложным после того, когда в Австралии были обнаружены черные лебеди. Научная индукция - такое умозаключение, в посылках которого наряду с повторяемостью признака у некоторых явлений класса содержится информация о зависимости этого признака от определенных свойств наблюдаемого явления.
Например, при изучении причин преступности среди несовершеннолетних можно взять сто первых попавшихся несовершеннолетних, проанализировать бюджет их свободного времени, уровень образования и на этом основании сделать общий вывод о причинах преступности несовершеннолетних всей области. Это - пример популярной индукции. Но можно поступить иначе. Можно произвести целевой отбор несовершеннолетних для исследования - исследовать определенный процент школьников, учащихся средних образовательных учреждений, техникумов, при этом отбирать эти категории несовершеннолетних из разных районов исследуемого региона. Индукция, в которой посылки готовятся по заранее подготовленному плану, по специально разработанным методикам, называется индукцией через отбор случаев.
Можно также изучить зависимость причин преступности от места учебы, места жительства, уровня образования, занятости на работе и т. д. Индукция, в которой общее заключение делается на основе знания внутренних связей между явлениями данного класса и законов, называется индукцией через установление причинных связей.[2]
2.Условно-категорический силлогизм и его правильные модусы. Утверждающий модус, отрицающий модус. Разделительно-категорический силлогизм. Утверждающе - отрицательный и отрицающее - утверждающий модусы, их правила.
Условно – категорический силлогизм – это умозаключение, в котором одна из посылок – условное суждение, а другая посылка и заключение – категорические суждения. Условно – категорический силлогизм имеет два правильных модуса: утверждающий (modus ponens) и отрицающий (modus tollens).[5, с.73]
В утверждающем модусе в категорической посылке утверждается истинность антецедента условной посылки, а в заключении – истинность консеквента. В данном случае рассуждение направлено от утверждения истинности основания к утверждению истинности следствия.[5, с.73] Схема утверждающего модуса:
Если есть А есть В, то С есть D,
А есть В,
Следовательно, С есть D.[4]
Например:
Для всякого проводника верно, что если по нему проходит ток, то он нагревается.
По проводнику проходит ток,
Следовательно, проводник нагревается.
В отрицающем модусе в категорической посылке отрицается истинность консеквента, а в заключении – истинность антецедента. Рассуждение построено от отрицания истинности следствия к отрицанию истинности основания.[5, с.73] Схема отрицающего модуса:
Если А есть В, то С есть D,
С не есть D,
Следовательно, А не есть B.[4]
Например:
Для всякого проводника верно, что если по нему проходит ток,
То он нагревается.
Проводник не нагревается.
Следовательно, по проводнику не проходит ток.
В условно-категорическом силлогизме есть еще два модуса.
Во-первых, от отрицания истинности основания к отрицанию истинности следствия.
Во-вторых, от утверждения истинности следствия к утверждению истинности основания.
Эти два модуса являются вероятностными: они не гарантируют истинность заключения при истинности посылок, за одним однако исключением – истинность заключения будет гарантирована в случае, если место импликативных суждений займут условные суждения эквивалентности.[5, с.74]
Разделительно-категорический силлогизм – это умозаключение из двух и более посылок, из которых, по крайней мере, одна – разделительное суждение, а остальные – категорические. Разделительно-категорический силлогизм имеет два модуса: утверждающе-отрицательный (modus ponendo tollens) и отрицающе-утверждающий (modus tollendo ponento).[5, с.75]
Modus ponendo tollens – умозаключение, большая посылка которого является разделительным суждением, меньшая – утвердительным суждением, а вывод – отрицательным суждением.[4]
Схема утверждающе-отрицающего модуса:
Каждое А есть либо В, либо С,
А есть В,
Следовательно, А не есть В.[4]
Например:
Все существа либо, люди, либо животные,
Данное существо есть человек,
Следовательно, оно не есть животное.
Суть данного модуса в том, что в категорической посылке производится утверждение одной альтернативы разделительного суждения, а в заключении отрицаются все остальные альтернативы. [5, с.75]
Правило modus ponendo tollens – разделительная посылка должна быть строгой (исключающей) дизъюнкцией.[5, с.75]
Modus tollendo ponento – умозаключение, большая посылка которого является разделительным суждением, меньшая – отрицательным суждением, а вывод – положительным суждением.[4]
Схема отрицающе-утверждающего модуса:
Каждое А есть либо В, либо С,
Данное А не есть В,
Следовательно, данное А есть С.[4]
Например:
Все дети или мальчики, или девочки,
Данный ребенок не мальчик,
Следовательно, этот ребенок девочка.
Суть данного модуса в том, что в категорической посылке производится отрицание всех членов дизъюнкции, кроме одного, истинность которого утверждается в заключении. В данном случае дизъюнкция может быть как строгой, так и нестрогой. [5, с.76]
Правило modus tollendo ponento - в разделительной посылке должны быть перечислены все возможные варианты.[5, с.76]
Фигурами силлогизма называются формы силлогизма, отличающиеся расположением среднего термина в посылках:
|
Фигура 1 |
Фигура 2 |
Фигура 3 |
Фигура 4 |
|||||
|
Большая посылка: |
M—P |
P—M |
M—P |
P—M |
||||
|
Меньшая посылка: |
S—M |
S—M |
M—S |
M—S |
||||
|
Заключение: |
S—P |
S—P |
S—P |
S—P |
Каждой фигуре отвечают модусы — формы силлогизма, различающиеся количеством и качеством посылок и заключения. Модусы изучались ещё средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена[6]:
|
Фигура 1 |
Фигура 2 |
Фигура 3 |
Фигура 4 |
|||
|
Barbara |
Cesare |
Darapti |
Bramantip |
|||
|
Celarent |
Camestres |
Disamis |
Camenes |
|||
|
Darii |
Festino |
Datisi |
Dimaris |
|||
|
Ferio |
Baroco |
Felapton |
Fesapo |
|||
|
Bocardo |
Fresison |
|||||
Примеры силлогизмов каждого типа: (см. приложение 1)
Практическое задание
3.Данной схеме соответствует следующая группа понятий:
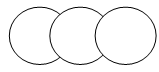
А)мальчик, девочка, школьник;
Б)студент, спортсмен, преподаватель;
В)врач, отец, бизнесмен;
Г)вуз, московский вуз, ВЗФЭИ.
Ответ: в задании представлены круги Леонардо Эйлера. Ответом на данное задание будут буквы Б) и В), т.к. не все студенты спортсмены и не все спортсмены студенты, так же как не все спортсмены преподаватели и не все преподаватели являются спортсменами; многие врачи стали отцами, но не все отцы по профессии врачи, у кого-то отец-бизнесмен, у кого-то нет.
Заключение
Целью данной работы было изучить подробно индуктивные умозаключения, условно-категорический и разделительно-категорический силлогизмы и их модусы.
Разбирая эти темы, можно сделать вывод, что большую часть знаний о предметах и явлениях окружающего мира человек получает из уже имеющейся у него информации, которую он в дальнейшем использует для изучения нового при этом он использует индуктивное умозаключение.
Сам того не замечая человек каждый день использует категорический силлогизм – рассуждение мысли.
Подводя итоги работы, можно сказать, что цель, поставленная вначале, была выполнена.
Список использованной литературы
1.Учебно-методический комплекс «Логика»: Учебно-методическое пособие для студентов гуманитарных факультетов / Науч.ред. А.А. Хачатрян. – Волгоград: ВолГУ, 2003. – 124с.
2.Индуктивные умозаключения // БГУИР: Дистанционное и Заочное обучение [Электронный ресурс], режим доступа: http://bsuir.info/load/50-1-0-3235, свободный, (дата обращения: 7.04.2013).
3.Индуктивное умозаключение // Свободная энциклопедия «Википедия» [Электронный ресурс], режим доступа: http://ru.wikipedia.org/wiki/, свободный, (дата обращения: 7.04.2013).
4.Информационно-аналитический портал. Православие и современность. Электронная библиотека. Курс русской риторики: Глава 2. Изобретение. Умозаключение. / А.А. Волков. [Электронный ресурс], режим доступа: http://lib.eparhia-saratov.ru/books/03v/volkov/ritorika/97.html, свободный, (дата обращения: 7.04.2013)
5.Логика: учебное пособие / М.Д. Купарашвили, А.В. Нехаев, В.И. Разумов, Н.А. Черняк. – Омск: ОмГУ, 2004. – 124с.
6.Категорический силлогизм // Свободная энциклопедия «Википедия» [Электронный ресурс], режим доступа: http://ru.wikipedia.org/wiki/, свободный, (дата обращения: 7.04.2013).
Приложение 1
Примеры силлогизмов каждого типа[6]:
Barbara
Все животные смертны.
Все люди — животные.
Все люди смертны.
Celarent
Ни одна рептилия не имеет меха.
Все змеи — рептилии.
Ни одна змея не имеет меха.
Darii
Все котята игривые.
Некоторые домашние животные — котята.
Некоторые домашние животные — игривые.
Ferio
Ни одна домашняя работа не весела.
Некоторое чтение — домашняя работа.
Некоторое чтение не весело.
Cesare
Ни одна здоровая еда не полнит.
Все торты полнят.
Ни один торт не здоровая еда.
Camestres
Все лошади имеют вздутие живота.
Ни один человек не имеет вздутия живота.
Ни один человек не лошадь.
Festino
Ни один ленивый человек не сдаёт экзамены.
Некоторые студенты сдают экзамены.
Некоторые студенты не ленивы.
Baroco
Все информативные вещи полезны.
Некоторые сайты не полезны.
Некоторые сайты не информативны.
Darapti
Все фрукты питательны.
Все фрукты вкусны.
Некоторые вкусные продукты питательны
Disamis
Некоторые кружки красивы.
Все кружки полезны.
Некоторые полезные вещи красивы.
Datisi
Все прилежные мальчики в этой школе рыжие.
Некоторые прилежные мальчики в этой школе — пансионеры.
Все прилежные мальчики пансионеры в этой школе рыжие.
Felapton
Ни один кувшин в этом шкафу не нов.
Все кувшины в этом шкафу треснутые.
Некоторые треснутые вещи в этом шкафу не новы.
Bocardo
Некоторые кошки бесхвосты.
Все кошки — млекопитающие.
Некоторые млекопитающие бесхвосты.
Ferison
Ни одно дерево не съедобно.
Некоторые деревья зелёные.
Некоторые зелёные вещи не съедобны.
Bramantip
Все яблоки в моём саду полезны.
Все полезные фрукты зрелы.
Некоторые зрелые фрукты — яблоки в моём саду.
Camenes
Все яркие цветы ароматны.
Ни один ароматный цветок не выращен в помещении.
Ни один выращенный в помещении цветок не ярок.
Dimaris
Некоторые небольшие птицы питаются мёдом.
Все питающиеся мёдом птицы цветные.
Некоторые цветные птицы небольшие.
Fesapo
Ни один человек не совершенен.
Все совершенные существа мифические.
Некоторые мифические существа не люди.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Индуктивные умозаключения [20.05.13]](/files/works_screen/1/44/79.png)