Контрольная работа по Методам оптимальных решений Вариант №3

Тема: Контрольная работа по Методам оптимальных решений Вариант №3

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 146.26K | Скачано: 380 | Добавлен 01.05.13 в 18:11 | Рейтинг: +1 | Еще Контрольные работы

Вуз: Финансовый университет

Год и город: Курск 2013

Задача 1

Решить графическим методом типовую задачу оптимизации

Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. Ед., а улучшенный – 4 ден. Ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?

Решение:

Сформулируем прямую оптимизационную задачу.

Пусть х₁ – количество обычных наборов удобрений;

х₂ – количество улучшенных наборов удобрений.

Содержание в двух данных наборах азотных удобрений: 3х₁ + 2х₂

А для некоторого газона требуется по крайней мере 10 кг азотных удобрений, следовательно:

3х₁ + 2х₂ ≥ 10

Содержание в двух данных наборах фосфорных удобрений должно быть не менее 20 кг, т.е.:

4х₁ + 6х₂ ≥ 20

И содержание в двух данных наборах калийных удобрений должно быть не менее 7 кг, т.е.:

1х₁ + 3х₂ ≥ 7

Стоимость необходимых наборов удобрений составит:

3х₁ + 4х₂.

Таким образом, получим следующую экономико-математическую модель задачи:

min ¦(х) = 3х₁ + 4х₂

3х₁ + 2х₂ ≥ 10

4х₁ + 6х₂ ≥ 20

х₁ + 3х₂ ≥ 7

х₁ ³ 0, х₂ ³ 0

Построим область решений системы ограничений. Для этого рассмотрим равенства и построим их графики – прямые.

(1) 3х₁ + 2х₂ ≥ 10

      3х₁ + 2х₂ = 10

х1	х2
0	5
4	-1

Для нахождения полуплоскости, соответствующей данному неравенству, берем любую точку, не лежащую на граничной прямой, и подставляем ее координаты в неравенство.

Возьмем точку О(0;0):

3*0 + 2*0 ≥ 10

0 ≥ 10

Неравенство не выполняется, значит, исходному неравенству соответствует та полуплоскость, которая не содержит точку (0;0).

(2) 4х₁ + 6х₂ ≥ 20

      4х₁ + 6х₂ = 20

х1	х2
-1	4
5	0

4*0 + 6*0 ³ 20

0 ³ 20

Неравенство не выполняется, значит, исходному неравенству соответствует полуплоскость, не содержащая точку О(0;0).

(3) х₁ + 3х₂ ≥ 7

      х₁ + 3х₂ = 7

х1	х2
-2	3
7	0

1*0 + 3*0 ³ 7

0 ³ 7

Неравенство не выполняется, значит, исходному неравенству соответствует полуплоскость, не содержащая точку О(0;0).

(4) х₁ ³ 0

     х₁ = 0 – ось ОХ₂.

(5) х₂ ³ 0

     х₂ = 0 – ось ОХ₁.

Следовательно, область решений системы ограничений находится только в первой четверти декартовой системы координат.

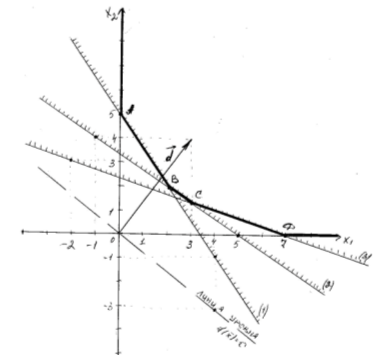
Рис.1. Графическое решение ЗЛП

Находим общую часть всех построенных полуплоскостей. Это выпуклая область с четырьмя угловыми точками А, В, С и Д.

Для нахождения оптимального решения задачи изобразим графически функцию цели:

¦(х) = d₁x₁ + d₂x₂

¦(х) = 3х₁ + 4х₂

Для этого строим вектор d, начало которого в точке (0;0), а конец в точке (d₁;d₂).

d = (3; 4).

И строим одну из линий уровня функции цели (это линия, на которой функция цели принимает постоянное значение).

¦(х) = d₁x₁ + d₂x₂ = а;    а – const.

Пусть а = 0, тогда ¦(х) = 3х₁ + 4х₂ = 0

х1	у
0	0
4	-3

Для определения минимума данной функции, передвигаем линию уровня в направлении, противоположном вектору d, и видим, что она последний раз соприкасается с областью решений в точке В, где и будет достигнут min¦(х).

Определим координаты точки В:

3х₁ + 2х₂ = 10   *(-3)

4х₁ + 6х₂ = 20          

-9х₁ – 6х₂ = -30  я

 4х₁ + 6х₂ = 20          

Складываем почленно уравнения и получаем:

-5х₁ = -10

х₁ = 2

В(2; 2)

max ¦(х) = 3*2 + 4*2 = 14 (ден. ед.)

Таким образом, чтобы минимизировать стоимость удобрений, нужно купить 2 обычных набора удобрений и 2 улучшенных набора удобрений. При этом минимальные затраты на покупку удобрений составят 14 денежных единиц.

Если решать данную задачу на максимум, то конечного оптимума не найдем, т.к. функция цели неограниченна, область решений системы ограничений бесконечна.

 

Задача 2

 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования

Для изготовления четырех видов продукции используется три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

Тип сырья	Нормы расхода сырья на одно изделие				Запасы сырья
	А	Б	В	Г
I	2	1	3	2	200
II	1	2	4	8	160
III	2	4	1	1	170
Цена изделия	5	7	3	6

Требуется:

1. Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.

2. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.

3. Пояснить нулевые значения переменных в оптимальном плане.

4. На основе свойств двойственных оценок и теорем двойственности:

- проанализировать использование ресурсов в оптимальном плане исходной задачи;

- определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно и уменьшении на 5 ед. запасов сырья III вида;

- оценить целесообразность включения в план изделия Д це­ной 10 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.

Решение:

1. Сформулируем прямую оптимизационную задачу.

Пусть х₁ – количество продукции вида А;

           х₂ – количество продукции вида Б;

           х₃ – количество продукции вида В;

           х₄ – количество продукции вида Г.

mах ¦(х) = 5x₁ + 7x₂ + 3x₃ + 6x₄ – общая стоимость продукции;

2x₁ + x₂ + 3x₃ + 2x₄ ≤ 200 

левая часть – расход сырья I типа на производство всей продукции

правая часть (200 ед.) – запас сырья I типа

x₁ + 2x₂ + 4x₃ + 8x₄ ≤ 160

левая часть – расход сырья II типа на производство всей продукции

правая часть (160 ед.) – запас сырья II типа

2x₁ + 4x₂ + x₃ + x₄ ≤ 170

левая часть – расход сырья III типа на пр-во всей продукции

правая часть (170 ед.) – запас сырья III типа

x_j ³ 0 (j = 1,2,3,4)

Оптимальный план задачи получим с помощью надстройки Excel Поиск решения (см. приложение 1).

Таким образом, получен оптимальный план:

x₁ = 80

x₂ = 0

x₃ = 0

x₄ = 10

mах ¦(х) = 460 (ден. ед.)

Т.е. максимальный доход в 460 денежных единиц можно получить, если продукции вида А выпустить 80 единиц, вида Г – 10 ед.; вида Б и В не выпускать (т.к. х₂ = 0 и х₃ = 0); при этом ресурсы II и III типа используются полностью, а ресурс I не полностью, его остаток составляет 20 ед.

2. Сформулируем двойственную задачу.

	2	1	3	2	200
А =	1	2	4	8	160
	2	4	1	1	170
	5	7	3	6	mах ¦(х)

	2	1	2	5
	1	2	4	7
А' =	3	4	1	3
	2	8	1	6
	200	160	170	min g(у)

у_i – цена единицы ресурса i-го типа (i = 1,2,3)

min g(у) = 200у₁ + 160у₂ + 170у₃ – общая стоимость ресурсов

2у₁ + у₂ + 2у₃ ≥ 5

левая часть - стоимость ресурсов, расходуемых на производство

одного изделия вида А (если предприятие решило

продать имеющиеся ресурсы)

правая часть – сумма, которую предприятие может получить при

переработке сырья в готовую продукцию

у₁ + 2у₂ + 4у₃ ≥ 7

стоимость ресурсов, идущих на пр-во одного изделия вида Б

3у₁ + 4у₂ + у₃ ≥ 3

стоимость ресурсов, идущих на пр-во одного изделия вида В

2у₁ + 8у₂ + у₃ ≥ 6

стоимость ресурсов, идущих на прво одного изделия вида Г

у₁, у₂, у₃ ³ 0

Найдем оптимальное решение двойственной задачи, используя вторую теорему двойственности:

х_j * (∑а_ijy_j – c_j) = 0        (j = 1,n)

y_i * (∑a_ijx_j – b_i) = 0       (i = 1,m)

х₁ = 80    80*(2у₁ + у₂ + 2у₃ - 5) = 0

             2у₁ + у₂ + 2у₃ - 5 = 0

             2у₁ + у₂ + 2у₃ = 5

х₂ * (у₁ + 2у₂ + 4у₃ - 7) = 0

х₂ = 0    0*( у₁ + 2у₂ + 4у₃ - 7) = 0       Вывода нет

х₃ * (3у₁ + 4у₂ + у₃ - 3) = 0

х₃ = 0    0*( 3у₁ + 4у₂ + у₃ - 3) = 0       Вывода нет

х₄ * (2у₁ + 8у₂ + у₃ - 6) = 0

х₄ = 10    80*(2у₁ + 8у₂ + у₃ - 6) = 0

2у₁ + 8у₂ + у₃ - 6 = 0

2у₁ + 8у₂ + у₃ = 6

у₁ * (2x₁ + x₂ + 3x₃ + 2x₄ - 200) = 0

у₁ * (2*80 + 1*0 + 3*0 + 2*10 - 200) = 0

у₁ * (180 – 200) = 0  

у₁ * (-20) = 0

у₁ = 0

у₂ * (x₁ + 2x₂ + 4x₃ + 8x₄ - 160) = 0

у₂ * (1*80 + 2*0 + 4*0 + 8*10 - 160) = 0

у₂ * 0 = 0   Вывода нет

у₃ * (2x₁ + 4x₂ + x₃ + x₄ - 170) = 0

у₃ * (2*80 + 4*0 + 1*0 + 1*10 - 170) = 0

у₃ * 0 = 0   Вывода нет

2у₁ + у₂ + 2у₃ = 5

2у₁ + 8у₂ + у₃ = 6

у₁ = 0

у₂ + 2у₃ = 5

8у₂ + у₃ = 6      *(-2)

    у₂ + 2у₃ = 5

-16у₂ - 2у₃ = -12

-15у₂ = -7

у₂ =

у₃ =

у = (0; ; )

g(у) = 200*0 + 160* + 170* = 460

max g(у) = min ¦(х) = 460

Следовательно, у = (0; ; ) – оптимальный план двойственной задачи.

3. Поясним нулевые значения переменных в оптимальном плане.

x₂ = 0

x₃ = 0

Т.е. продукцию вида Б и В выпускать не следует, т.к. их выпуск не приведет к максимальной выручке от реализации готовой продукции.

4. Проанализируем использование ресурсов в оптимальном плане.

Оценим использование ресурсов:

I типа: 2*80 + 1*0 + 3*0 + 2*10 = 180 < 200 – сырье I типа используется не полностью, остаток составляет 20 ед.; х₅ = 20

II типа: 1*80 + 2*0 + 4*0 + 8*10 = 160 = 160 – сырье II типа используется полностью; х₆ = 0

III типа: 2*80 + 4*0 + 1*0 + 1*10 = 170 = 170 – сырье III типа используется полностью; х₇ = 0

х = (80, 0, 0, 10, 20, 0, 0)

Т.к. у₁ = 0, то ресурс I типа используется не полностью.

Т.к. у₂ > 0 и у₃ > 0, то ресурсы II и III типов используются полностью. При чем ресурс III типа является более ценным, более дефицитным, чем ресурс II типа, т.к. у₃ > у₂.

Определим, как изменится выручка и план выпуска продукции, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа

Δb₁ = 8

Δb₂ = 10

Δb₃ = -5

Δ¦(х) = ∑y_i Δb_i

Δ¦(х) =  

Значит, выручка от реализации продукции уменьшится на  денежных единиц и составит   ден. ед.

Изменение плана выпуска продукции ΔХ находим следующим образом:

ΔХ = Д * ΔВ

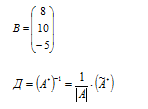
Матрица А^* состоит из столбцов матрицы А (канонической формы), которые соответствуют основным переменным.

х = (80, 0, 0, 10, 20, 0, 0)

	2	1	3	2	1	0	0
А =	1	2	4	8	0	1	0
	2	4	1	1	0	0	1

	2	2	1
А* =	1	8	0
	2	1	0

Определитель матрицы А^* равен:

|А^*| = 0 + 0 + 1 – (16 + 0 + 0) = -15

Транспонируем матрицу А^*:

	2	1	2
(А*)’ =	2	8	1
	1	0	0

Находим элементы присоединенной матрицы (Ã^*):

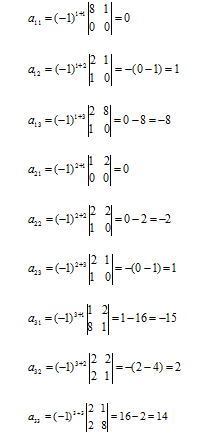
Получили присоединенную матрицу:

	0	1	-8
(Ã*) =	0	-2	1
	-15	2	14

 

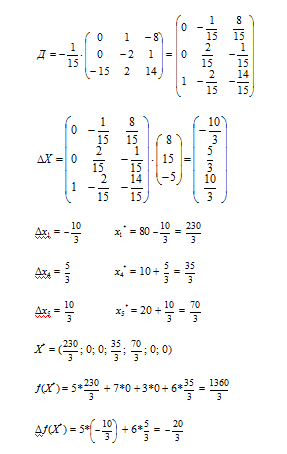
Таким образом, при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно и уменьшении на 5 ед. запасов сырья III вида выпуск продукции вида А уменьшится на  ед., вида Г – увеличится на  ед. Остаток сырья I вида увеличится на  ед.

Определим целесообразность включения в план изделия Д ценой 10 единиц, на изготовление которого расходуется по две единицы каждого вида сырья.

С₅ = 10

а₁₅ = 2;   а₂₅ = 2;   а₃₅ = 2

Δ_j = ∑а_ijy_j – c_j        

Δ₅ = а₁₅y₁ – а₂₅y₂ – а₃₅y₃ – c₅

Δ₅ =

Δ₅ < 0, следовательно изделие вида Д выпускать выгодно.

Так как затраты на ресурсы при выпуске одного данного изделия вида Д будут меньше цены изделия вида Д.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Контрольная работа по Методам оптимальных решений Вариант №3
• Методы линейного программирования, двойственность в ЛП
• Контрольная работа по Методам оптимальных решений Вариант №3