Применение теории графов в информатике

Тема: Применение теории графов в информатике

Раздел: Бесплатные рефераты по информатике

Тип: Курсовая работа | Размер: 219.92K | Скачано: 303 | Добавлен 06.04.13 в 16:13 | Рейтинг: +2 | Еще Курсовые работы

Оглавление

Введение 2

1. Теоретическая часть 3

1.1. История возникновения теории графов 4

1.2. Терминология теории графов и основные виды графов 5

1.3. Способы представления графа в ЭВМ, языки описания и программы построения графов 9

Заключение 14

Практика 15

Список литературы 23

 

Введение

Теория графов — раздел дискретной математики, изучающий свойства графов. Она применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электроника, машиностроение, архитектура, исследование операций, генетика, психология, социология, экономика, антропология и лингвистика. При этом обычно на графе решаются задачи о достижимости, задачи сетевого планирования, потоковая задача.

Интерес к проблемам теории графов был сосредоточен главным образом в Англии. Имелось много причин для такого оживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса.

Изучение теории графов является актуальным, так как настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии. Вследствие этого развития предмет теории графов является уже обширным.

Основную проблему в применении теоретико-графовых методов составляет проблема терминологии, так как она далеко не устоялась.

Целью данной работы является подробное рассмотрение теории графов в информатике, выявление их сущности, изучение терминологии, а также способы представления графов в ЭВМ.

 

1. Теоретическая часть

1.1. История возникновения теории графов

В начале XVIII века в городе Кёнигсберге (в настоящее время Калининград) было семь мостов. На рис.1.1. показано изображение центральной части города Кенигсберг. Река Преголя делит Кёнигсберг на четыре несвязанные части A, B, C и D. Различные части города соединены между собой семью мостами.

Возник вопрос: можно ли обойти все семь мостов, побывав на каждом по одному разу? Этот вопрос был предложен знаменитому математику Леонарду Эйлеру(1707-1783), которого впоследствии принято считать родоначальником теории графов. Рассмотрев эту задачу, в 1736 году Эйлер доказал, что это невозможно [2, с.13].

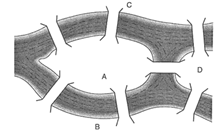
Рис.1.1. Изображение Кёнигсбергских мостов

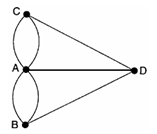
Рис.1.2. Упрощенная схема Кёнигсбергских мостов (граф)

Эйлер взял план города и заменил его упрощенной схемой (рис.1.2.). На схеме мостам соответствуют линии (рёбра графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

• Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа всегда чётно. Невозможно начертить граф, который имел бы нечётное число нечётных вершин.
• Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
• Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.

Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно,  невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

 

1.2. Терминология теории графов и основные виды графов

Теория графов не обладает устоявшейся терминологией. В разных статьях под одними и теми же терминами понимаются разные вещи. В частности в монографии Гудман, Хидетниеми, 1981 г.  сказано: «В программистском мире нет единого мнения о том, какой из двух терминов „граф“ или „сеть“. Мы выбрали термин „сеть“, так как он, по-видимому, чаще встречается в прикладных областях». Аналогичная ситуация для «вершина/точка». Рассмотрим наиболее часто встречаемые определения [3, с. 21].

В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.

В строгом определении граф или неориентированный граф G — это упорядоченная пара G: = (V,E), для которой выполнены следующие условия: V - это множество вершин или узлов, E - это множество пар (в случае неориентированного графа — неупорядоченных) различных вершин, называемых рёбрами. Неориентированный граф представлен на рис.1.2.1.[7].

Рис.1.2.1. Неориентированный граф

Вершины и рёбра графа называются также элементами графа, число вершин в графе | V |  — порядком, число рёбер | E |  — размером графа.

Вершины  и  называются концевыми вершинами (или просто концами) ребра . Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.

Два ребра называются смежными, если они имеют общую концевую вершину.

Два ребра называются кратными, если множества их концевых вершин совпадают.

Ребро называется петлей, если его концы совпадают, то есть  .

Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды). Инцидентность — понятие, используемое только в отношении ребра и вершины: если v₁,v₂ — вершины, а e = (v₁,v₂) — соединяющее их ребро, тогда вершина v₁ и ребро e инцидентны, вершина v₂ и ребро e тоже инцидентны. Две вершины (или два ребра) инцидентными быть не могут. Для обозначения ближайших вершин (рёбер) используется понятие смежности.

Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер.

Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.

Граф называется:

• , если для любых вершин u,v есть путь из u в v.
• сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.
• деревом, если он связный и не содержит простых циклов.
• , если любые его две (различные, если не допускаются петли) вершины соединены ребром.
• двудольным, если его вершины можно разбить на два непересекающихся подмножества V₁ и V₂ так, что всякое ребро соединяет вершину из V₁ с вершиной из V₂.
• , если его вершины можно разбить на k непересекающихся подмножества V₁, V₂, …, V_k так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
• полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
• , если граф можно изобразить диаграммой на плоскости без пересечений рёбер.
• , если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках (Оре) и просто рёбрами. На рис. 1.2.2. изображен ориентированный граф.

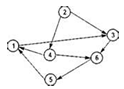
Рис.1.2.2. Ориентированный граф

Орграф D=(V, E) –  множество E упорядоченных пар вершин  . Дуга {u, v} инцидентна вершинам u и v. При этом говорят, что u — начальная вершина дуги, а v — конечная вершина.

Орграф, полученный из простого графа ориентацией ребер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.

Направленный полный граф называется турниром.

Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида v₀{v₀,v₁}v₁{v₁,v₂}v₂...v_n  ,(вершины могут повторяться). Длина маршрута – количество дуг в нем.

Путь – маршрут в орграфе без повторяющихся дуг, простой путь – без повторяющихся вершин. Если существует путь из одной вершины в другую, то такая вершина достижима из первой.

Ориентированным путём в орграфе называют конечную последовательность вершин v_i , для которой все пары (v_i,v_{i + 1}) являются (ориентированными) рёбрами.

Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.

Контур – замкнутый путь.

Орграф сильно связный, или просто сильный если все его вершины взаимно достижимы; односторонне связный, или просто односторонний если для любых двух вершин, по крайней мере одна достижима из другой; слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;

Конденсацией орграфа D называют орграф D*, вершинами которого служат сильные компоненты D, а дуга в D* показывает наличие хотя бы одной дуги между вершинами, входящими в соответствующие компоненты.

Существует такой вид графов как направленный ациклический граф – это случай направленного графа, в котором отсутствуют направленные циклы, то есть пути, начинающиеся и кончающиеся  в одной и той же вершине. Направленный ациклический граф является обобщением дерева.

Дерево – это связный ациклический граф, то есть, не содержащий циклов, между любой парой вершин которого существует ровно один путь.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

Смешанные графы — граф, в котором встречаются как ориентированные, так и неориентированные рёбра и петли.

Эйлеровы графы — граф, в котором существует циклический эйлеров путь (Эйлеров цикл).

Мультиграфы — графы с кратными рёбрами, имеющими своими концами одну и ту же пару вершин.

Псевдографы — это мультиграфы, допускающие наличие петель.

Простые графы — не имеющие петель и кратных рёбер.

Гиперграф — если ребро может соединять более двух вершин.

Ультраграф — если между элементами xi и uj существуют бинарные отношения инцидентности.

Графы G’ и G’’ называются изоморфными, если существует взаимнооднозначное соответствие (биекция) между их ребрами и вершинами, причем ребра соединяют соответствующие вершины.

Изоморфизм графов означает, что можно так переобозначить вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом. Все три графа изображенные на рис.1.2.3. изоморфны друг другу (изоморфизм определяется нумерацией вершин). 

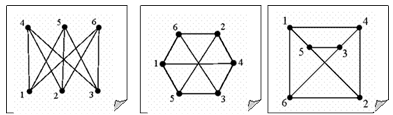
Рис.1.2.3. Изоморфные графы 

 

1.3. Способы представления графа в ЭВМ, языки описания и программы построения графов

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Выбор наилучшего представления определяется требованиями конкретных задач при решении которых используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они так или иначе основаны на четырех базовых идеях с указанием характеристики n(p,q) - объема памяти для каждого представления, где p - число вершин, а q - число ребер.

Для того чтобы применять ЭВМ для реализации алгоритмов анализа графов, нужно иметь возможность представлять в памяти компьютера необходимую для этой цели информацию. Непосредственное представление графа в виде точек и линий для современных ЭВМ не является удобным. Обычно для этой цели используются описания графа с помощью различных матриц.

1. Матрица смежности.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу рёбер из i-й вершины графа в j-ю вершину [5, с. 79]. На рис.1.3.1 и 1.3.2. приведен пример неориентированного графа и соответствующей ему матрицы смежности.

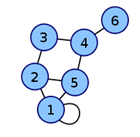
Рис.1.3.1. Неориентированный граф.

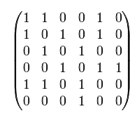
Рис.1.3.2. Матрица смежности.

Матрица смежности простого графа является бинарной матрицей и содержит нули на главной диагонали.

Использование матрицы смежности предпочтительно только в случае неразрежённых графов, с большим числом ребёр, так как она требует хранения по одному биту данных для каждого элемента. Если граф разрежён, то большая часть памяти напрасно будет тратиться на хранение нулей, зато в случае неразрежённых графов матрица смежности достаточно компактно представляет граф в памяти, используя примерно n / 8 байт памяти.

2. Списки смежности.

 Представление графа с помощью матрицы смежностей зачастую неудобно, поскольку количество вершин требуется знать заранее. Если граф должен создаваться или изменяться во время исполнения программы, то для каждого добавления или удаления вершины необходимо строить новую матрицу. Кроме того, даже если граф содержит малое число ребер (дуг) и матрица смежностей состоит в основном из нулей, память должна быть отведена для всех возможных дуг вне зависимости от того, существуют ли они. Если граф содержит n вершин, то должна быть отведена память для n² элементов. В этом случае следует применить списки смежности.

Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин (для орграфа — список вершин, являющихся концами исходящих дуг). Наиболее целесообразно применять этот способ для задания орграфов, однако и для остальных вариантов он тоже подходит. Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.  На рис.1.3.3. и 1.3.4. изображен орграф и соответствующий ему список смежности.

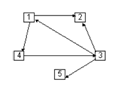
Рис.1.3.3. Ориентированный граф.

Рис.1.3.4. Список смежности.

3. Матрица инцидентности.

Матрицей инцидентности ориентированного (или неориентированного ) графа G=(V,E) с n вершинам и V= { v₁, ... , v_n} и m ребрами E={e₁, ..., e_m} называется матрица B_G размера n x m с элементами:

Каждая строка соответствует определённой вершине графа, а столбцы соответствуют связям графа. В ячейку на пересечении i-ой строки с j-м столбцом матрицы записывается: 1 – в случае, если связь j«выходит» из вершины i, −1 – если связь «входит» в вершину, 0 – если связь не инцидентна вершине. Ребра или петли выделяются числом 2. Для проверки наличия ребра между двумя вершинам и vi и vk требуется просмотреть i -ую и k -ую строки BG, поиск всех соседей вершины требует просмотра соответствующей строки. Если m >> n, то это требует существенно больше времени, чем при использовании матрицы смежности. Поэтому при практическом решении задач на графах матрица инцидентности почти не используется.

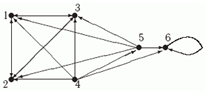
Рис.1.3.5. Ориентированный граф.

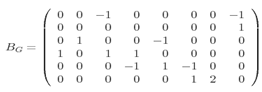
Рис.1.3.6. Матрица инцидентности. 

На рис.1.3.3 и 1.3.4 изображен ориентированный граф и соответствующая ему матрица инцидентности.

4. Список рёбер — это тип представления графа в памяти компьютерной программы, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности [5, с. 113]. На рис.1.3.5. приведен пример графов и их списков ребер.

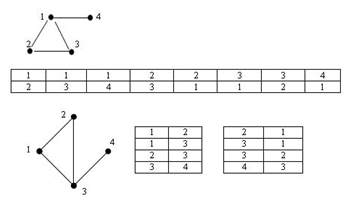
Рис.1.3.7. Графы и соответствующие им списки ребер.

Наряду со способами представления графов в памяти компьютера существуют языки описания и программы построения графов. Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков, среди которых: DOT, GraphML, Trivial Graph Format, GML, GXL, XGMML, DGML [7].

DOT — это язык описания графов в виде простого текста. Граф, описанный на языке DOT, обычно представляет собой текстовый файл с расширением .gv или .dot в понятном для человека и обрабатывающей программы формате. В графическом виде графы, описанные на языке DOT, представляются с помощью специальных программ, например Graphviz.

GraphML — язык описания (иногда упоминается как отдельный формат файлов) графов на основе XML. Он включает базовый язык, предназначенный для описания структурных свойств графа и гибкий механизм расширения его расширения, что позволяет включать в описание графа данные специфичные для приложений.

Trivial Graph Format («простой формат графов», сокр. TGF) — простой формат файлов, основанный на тексте, для описания графов.

GXL и GML — форматы обмена графами. XGMML — язык описания графов, основанный на XML, близко связанный с GML.

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Графы применимы для представления любой информации, которую можно промоделировать в виде объектов и связей между объектами.

 

Заключение

Таким образом, современное состояние информатики и программирования нельзя представить себе без применения теоретико-графовых методов. Анализ программ, оптимизация, автоматическое распараллеливание, сложные структуры данных, отладка и тестирование, оценка сложности программ, повышение уровня параллелизма в программе — вот далеко не полный перечень областей применения теоретико-графовых методов в программировании. Сюда же можно добавить такие интенсивно развиваемые в последнее время направления, как проектирование сетей ЭВМ, сетей межпроцессорных связей, маршрутизация при пересылке данных в параллельных компьютерах с распределенной памятью, повышение эффективности работы с памятью, организация больших массивов информации. В теоретическом программировании важную роль играют различные теоретико-графовые модели программ и систем, включая системы переписывания графов и графовые грамматики. Активно используются методы теории графов в искусственном интеллекте.

Существует ряд способов представления графов в информатике: матрицы смежности, списки смежности, матрица инцидентности, список ребер. Для описания графов в целях, пригодных для машинной обработки и одновременно удобном для человеческого восприятия используется несколько стандартизированных языков: DOT, GraphML, Trivial Graph Format, GML, GXL, XGMML, DGML.

Теория графов стала активно применяться в программировании одновременно с использованием ЭВМ в силу удобного выражения задач обработки информации на теоретико-графовом языке.

 

2. Практическая часть

2.1. Общая характеристика задачи

Агентство по грузоперевозкам «Летучий голландец» предоставляет услуги по перевозке грузов по различным маршрутам. Данные о маршрутах, выполненных в течение недели, по каждому водителю приведены на рис.2.1.1. Справочные данные о технических характеристиках автомобилей и протяженности маршрутов приведены на рис.2.1.2.

1. Построить таблицы по приведенным ниже данным.
2. Выполнить расчет количества израсходованного топлива каждым водителем и веса перевезенного груза, данные расчета занести в таблицу (рис.2.1.1).
3. Организовать межтабличные связи для автоматического формирования ведомости расчета топлива за неделю.
4. Сформировать и заполнить ведомость расхода горючего каждым водителем за неделю (рис.2.1.3).
5. Результаты расчета количества израсходованного топлива за неделю представить в графическом виде.

Сведения о выполненных маршрутах

№ п/п	ФИО водителя	Марка автомобиля	№ рейса	Выполнено рейсов, шт.	Протяжен-ность рейса, км	Расход топлива на 100 км, л	Израсходовано топлива, л	Грузо-подъемность, т	Вес перевезенного груза, т
1	Соловьев В.В.	КАМАЗ	А112	4
2	Михайлов С.С	ЗИЛ	С431	3
3	Кузнецов Я.Я.	МАЗ	А112	5
4	Иванов К.К.	МАЗ	М023	7
5	Сидоров А.А.	ЗИЛ	В447	2
6	Волков Д.Д.	КАМАЗ	С431	8
7	Быков Л.Л.	КАМАЗ	В447	4
	ИТОГО	×	×	×
	В СРЕДНЕМ	×	×	×

Рис.2.1.1. Данные о выполненных маршрутах

Технические характеристики                               Протяженность

             автомобилей                                                   рейсов

№ п/п	Марка автомобиля	Расход топлива на 100 км, л	Грузо- Подъемность, т
1	ЗИЛ	42	7
2	КАМАЗ	45	16
3	МАЗ	53	12

№ п/п	№ рейса	Протяженность рейса, км
1	А112	420
2	В447	310
3	М023	225
4	С431	250

                                                                    

 

Рис.2.1.2. Технические характеристики автомобилей и данные о протяженности выполняемых рейсов

 

2.2. Описание алгоритма решения задачи смотрите в файле

 

Список литературы

1. Алексеев В. Б., Ложкин С. А. Элементы теории графов и схем.М.:МГУ. – 2007. - 40 с.
2. Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука. – 2008. - 384 с.
3. Костюкова Н. И. Графы и их применение. Комбинаторные алгоритмы для программистов. М: Интернет-университет информационных технологий, Бином. – 2007. – 312с.
4. Кристофидес Н.Теория графов. Алгоритмический подход. М.: Мир. – 2008.– 429c.
5. Липатов Е. П. Теория графов и ее применение. М: Знание. – 1986. – 367с.
6. Свами М., Тхулалираман К. Графы, сети и алгоритмы. М: Мир. – 2009. – 455с.
7. общедоступная мультиязычная универсальная интернет-энциклопедия –  http://www.wikipedia.org.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Курсовые работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Курсовые работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Курсовая работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Применение теории графов в информатике (понятия, задачи)
• Применение теории графов в информатике