Тема: Применение теории графов в информатике (понятия, задачи)

Раздел: Бесплатные рефераты по информатике

Тип: Курсовая работа | Размер: 380.05K | Скачано: 377 | Добавлен 14.06.11 в 19:00 | Рейтинг: 0 | Еще Курсовые работы

Вуз: ВЗФЭИ

Год и город: Владимир 2009

Содержание

Ведение 3

I. Теоретическая часть 5

1.1. История возникновения теории графов 5

1.2. Основные понятия теории графов 7

1.3. Способы представления графов в информатике 11

1.4. Обзор задач теории графов 13

II. Практическая часть 15

2.1. Общая характеристика задачи 15

2.2. Описание алгоритма решения задачи 18

Заключение 23

Список используемой литературы 24

 

Введение

Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок. Очень долго она находилась в стороне от главных направлений исследований ученых, была в царстве математики на положении Золушки, чьи дарования раскрылись в полной мере лишь тогда, когда она оказалась в центре общего внимания.

Целью работы является изучение теории графов применительно к информатике. Задачи курсовой работы:

• Изучение истории возникновения теории графов;
• Раскрытие основных понятий этой теории;
• Представление графов в компьютерном виде;
• Обзор задач теории графов.

Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.

Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем. Теория графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.

В практической  части курсовой работы будет решена задача о перевозке грузов по различным маршрутам.

  Для выполнения и оформления курсовой работы использовался следующий состав программного и технического обеспечения:

1. Программное обеспечение: ОС Windows XP; Текстовый редактор MS Word 2003; Табличный процессор MS Excel 2003.

2. Техническое обеспечение: процессор Intel Pentium IV; оперативная память 512Мб; постоянная память 20 Гб.

 

I.      Теоретическая часть

1.1 История возникновения теории графов

Родоначальником теории графов принято считать математика Леонарда Эйлера (1707-1783) [3, стр. 36]. Однако теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.

Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G=(V,E), где V есть подмножество любого счётного множества, а E — подмножество V×V.

При изображении графов чаще всего используется следующая система обозначений: каждой вершине сопоставляется точка на плоскости, и если между вершинами существует ребро, то соответствующие точки соединяются отрезком. В случае ориентированного графа отрезки заменяют стрелками.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет. В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

1. Задача о Кенигсбергских мостах. На рис. 1 представлен схематический план центральной части города Кенигсберг (ныне Калининград), включающий два берега реки Перголя, два острова в ней и семь соединяющих мостов. Задача состоит в том, чтобы обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку. Эта задача была решена (показано, что решение не существует) Эйлером в 1736 году.

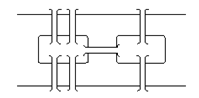
Рис. 1. Схематический план центральной части города Кенигсберг.

2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца, каким-то образом расположенные на плоскости. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 2). Эта задача была решена (показано, что решение не существует) Куратовским в 1930 году [2, стр. 51].

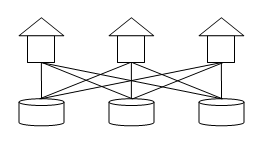
Рис.2. Задача о трех домах и трех колодцах.

 

1.2 Основные понятия теории графов.

1. G(V,E) называется совокупность двух множеств – непустого множества V(множества вершин) и множества E двухэлементных подмножеств множества V(E – множество ребер).
2. Ориентированным называется граф, в котором  - множество упорядоченных пар вершин вида (x,y), где x называется началом, а y – концом дуги. Дугу (x, y) часто записывают как . Говорят также, что дуга ведет от вершины x к вершине y, а вершина y смежная с вершиной x.
3. Если элементом множества E может быть пара одинаковых (не различных) элементов V, то такой элемент множества E называется петлей, а граф называется графом с петлями (или псевдографом).
4. Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.
5. Если элементами множества E являются не обязательно двухэлементные, а любые подмножества множества V, то такие элементы множества E называются гипердугами, а граф называется гиперграфом.
6. Если задана функция F : V → M и/или F : E → M, то множество M называется множеством пометок, а граф называется помеченным (или нагруженным). В качестве множества пометок обычно используются буквы или целые числа. Если функция F инъективна, то есть разные вершины (ребра)имеют разные пометки, то граф называют нумерованным.
7. Подграфом называется граф G′(V′,E′), где и/или .
   • Если V′ = V, то G′ называется основным подграфом G.
   • Если , то граф G′ называется собственным подграфом графа G.
   • Подграф G′(V′,E′) называется правильным подграфом графа G(V,E), если G′ содержит все возможные рёбра G.
8. Степень (валентность) вершины – это количество ребер, инцидентных этой вершине (количество смежных с ней вершин).
9. Маршрутом  в графе называется чередующаяся последовательность вершин и ребер , в которой любые два соседних элемента инциденты.
   • Если , то маршрут замкнут, иначе открыт.
   • Если все ребра различны, то маршрут называется цепью.
   • Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью.
   • Замкнутая цепь называется циклом.
   • Замкнутая простая цепь называетсяпростым циклом.
   • Граф без циклов называется ациклическим.
   • Для орграфов цепь называется путем, а цикл – контуром.

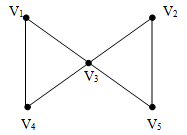
рис. 3. Маршруты, цепи, циклы

В графе, диаграмма которого приведена на рис.4:

1. ₁, v₃, v₁, v₄ – маршрут, но не цепь;
2. ₁, v₃, v₅, v₂, v₃, v₄ – цепь, но не простая цепь;
3. ₁, v₄, v₃, v₂, v₅ – простая цепь;
4. ₁, v₃, v₅, v₂, v₃, v₄, v₁ – цикл, но не простой цикл;
5. ₁, v₃, v₄, v₁ – простой цикл.
6. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом.
7. Если граф имеет простой цикл, содержащий все вершины графа (по одному разу), то такой цикл называется гамильтоновым циклом.
8. Деревом называется связный граф без циклов.
9. называется дерево, содержащее все вершины графа.
10. Паросочетанием называется множество ребер, в котором никакие два не смежны.
11. Паросочетание называется максимальным, если никакое его надмножество не является независимым.
12. Граф, в котором все вершины связаны, называется связным.
13. Граф, состоящий только из изолированных вершин, называется вполне несвязным.
14. Длиной маршрута называется количество ребер в нем (с повторениями).
15. между вершинами u и v называется длина кратчайшей цепи , а сама кратчайшая цепь называется геодезической.
16. Диаметром графа G называется длина длиннейшей геодезической.
17. вершины v в связном графе G(V,E) называется максимальное расстояние от   вершины v до других вершин графа G.
18. Радиусом графа G называется наименьший из эксцентриситетов вершин.
19. Вершина v называется центральной, если ее эксцентриситет совпадает с радиусом графа.
20. Множество центральных вершин называется центром графа.

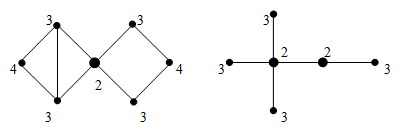
рис. 4.  Эксцентриситеты вершин и центры графов (выделены).

 

1.3. Способы представления графов в информатике

Конструирование структур данных для представления в программе объектов математической модели – это основа искусства практического программирования. Далее приводится четыре различных базовых представления графов. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении конкретных задач используются, как правило, некоторые комбинации или модификации указанных представлений, общее число которых необозримо. Но все они, так или иначе, основаны на тех базовых идеях, которые описаны в этом разделе.

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(p,q) – объема памяти для каждого представления. Здесь p – число вершин, а q – число ребер.

Матрица смежности

Представление графа с помощью квадратной нулевой матрицы M, отражающей смежность вершин, называется матрицей смежности, где

Для матрицы смежности n(p,q) = O(p²).

Замечание

Матрица смежности неориентированного графа симметрична относительно главной диагонали, поэтому достаточно хранить только верхнюю (или нижнюю) треугольную матрицу.

Матрица инциденций

Представление графа с помощью матрицы H, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

а для орграфа

Для матрицы инциденций n(p,q) = O(pq).

Списки  смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей на списки смежных вершин, где элемент списка представлен структурой

N : record v : 1..p; n :↑ N end record,

называется списком смежности. В случае представления неориентированных графов списками смежности n(p,q) = O(p+2q), а в случае ориентированных графов n(p,q) = O(p+q).

Массив дуг

Представление графа с помощью массива структур

E : array [1..q] of record b,e : 1..p end record,

отражающего список пар смежных вершин, называется массивом ребер (или, для орграфов, массивом дуг). Для массива ребер (или дуг) n(p,q) = O(2q).

 

1.4. Обзор задач теории графов

Развитие теории графов в основном обязано большому числу всевозможных приложений. По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем.[4, стр. 12-15]

Далее перечислим некоторые типовые задачи теории графов и их приложения:

- Задача о кратчайшей цепи

замена оборудования

составление расписания движения транспортных средств

размещение пунктов скорой помощи

размещение телефонных станций

- Задача о максимальном потоке

анализ пропускной способности коммуникационной сети

организация движения в динамической сети

оптимальный подбор интенсивностей выполнения работ

синтез двухполюсной сети с заданной структурной надежностью

задача о распределении работ

  - Задача об упаковках и покрытиях

оптимизация структуры постоянного запоминающего устройства       (ПЗУ)

размещение диспетчерских пунктов городской транспортной сети

  - Раскраска в графах

распределение памяти в ЭВМ

проектирование сетей телевизионного вещания

  - Связность графов и сетей

проектирование кратчайшей коммуникационной сети

синтез структурно-надежной сети циркуляционной связи

анализ надежности стохастических сетей связи

  - Изоморфизм графов и сетей

структурный синтез линейных избирательных цепей

автоматизация контроля при проектировании БИС

  - Автоморфизм графов

конструктивное перечисление структурных изомеров для производных органических соединений

синтез тестов цифровых устройств

 

I.  Практическая часть

2.1. Общая характеристика задачи

Агентство по грузоперевозкам «Летучий голландец» предоставляет услуги по перевозке грузов по различным маршрутам. Данные о маршрутах, выполненных в течение недели, по каждому водителю приведены на рис. 5. Справочные данные о технических характеристиках автомобилей и протяженность маршрутов приведены на рис. 6.

1. Построить таблицы по приведенным данным.
2. Выполнить расчет количества израсходованного топлива каждым водителем и веса перевезенного груза, данные расчета занести в таблицу (рис.5).
3. Организовать межтабличные связи для автоматического формирования ведомости расхода топлива за неделю.
4. Сформировать и заполнить ведомость расхода горючего каждым водителем за неделю (рис.7)
5. Результаты расчета количества израсходованного топлива за неделю представить в графическом виде.

Сведенья о выполненных маршрутах

№ п/п	ФИО	Марка авто	№ рейса	Выполненных рейсов, шт.	Протяженность рейса в км.	Расход топлива на 100км, л	Израсход топлива, л.	Грузоподъемность т	Вес перевезенного груза, т
1	Соловьев В.В	КАМАЗ	А112	4
2	Михайлов С.С	ЗИЛ	С 431	3
3	Кузнецов Я.Я	МАЗ	А112	5
4	Иванов К.К.	МАЗ	М 023	7
5	Сидоров А.А.	ЗИЛ	В 447	2
6	Волков Д.Д.	КАМАЗ	С 431	8
7	Быков Л.Л.	КАМАЗ	В 447	4
итого	*	*	*
В среднем	*	*	*

Рис.5. Данные о выполненных маршрутах

Техническая характеристика авто Протяженность рейсов

№ п/п	Марка авто	Расход топлива	Грузоподъемность
1	ЗИЛ	42	7
2	КАМАЗ	45	16
3	МАЗ	53	32

№ п/п	№ рейса	Протяженность
1	А 112	420
2	В 447	310
3	М 023	225
4	С 431	250

Рис. 6. Технические характеристики авто и данные о протяженности выполненных рейсов

Агентство по грузоперевозкам «Летучий голландец» Отчетный период С      По Ведомость расхода горючего ФИО № рейса Выполнено рейсов Израсходовано топлива Соловьев В.В       Михайлов С.С       Кузнецов Я.Я       Иванов К.К.       Сидоров А.А.       Волков Д.Д.       Быков Л.Л.       итого         Бухгалтер

Рис.7. Ведомость расхода горючего

 

2.2. Описание алгоритма решения задачи смотрите в файле

 

Заключение

По-видимому, из всех математических объектов графы занимают одно из первых мест в качестве формальных моделей реальных систем. В работе были рассмотрены задачи из теории графов, которые уже стали классическими. Особенно часто в практическом программировании возникают вопросы о построении кратчайшего остова графа и нахождении максимального паросочетания. Известно также, что задача о нахождении гамильтонова цикла принадлежит к числу NP-полных, т.е. эффективный алгоритм для ее решения не найден. Таким образом, задачи теории графов актуальны, так как могут принести экономию времени и средств на производстве и в быту.

Среди сложившихся разделов теории графов следует отметить задачи, относящиеся к анализу графов, определению различных характеристик их строения, например выяснение связности графа: можно ли из любой вершины попасть в любую; подсчёт графов или их частей, обладающих заданными свойствами, например подсчёт количества деревьев с заданным числом рёбер (дерево — неориентированный граф без циклов); решение транспортных задач, связанных с перевозками грузов по сети. Решен ряд задач по синтезу графов с заданными свойствами, например построение графа с заданными степенями вершин (степень вершины — число выходящих из неё рёбер).

Для некоторых задач теории графов (выше были приведены далеко не все) были разработаны методы их решения. Среди них: метод Пойя перечисления и подсчёта графов с заданными свойствами, теорема и алгоритм форда — фалкерсона для решения транспортной задачи, "венгерский" алгоритм решения задачи о назначениях и т. д. Теория графов содержит большое количество нерешённых проблем и пока недоказанных гипотез.

 

Список использованной литературы

1. Болтянский В.Г., Наглядная топология, М., Просвещение,2007.
2. Кордемский Б.А., Математическая смекалка, М., Физматгиз, 2006.
3. Кук Д., Бейз Г., Компьютерная математика, М., Наука, 2005.
4. Оре О., Графы и их применение, Новокузнецкий Физико-математический институт, 2007.
5. Информатика. Лабораторный практикум для студентов 2 курса всех специальностей. – М.: ВЗФЭИ, 2006.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Курсовые работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Курсовые работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Курсовая работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Применение теории графов в информатике
• Применение теории графов в информатике