Применение алгебры высказываний в информатике

Тема: Применение алгебры высказываний в информатике

Раздел: Бесплатные рефераты по информатике

Тип: Курсовая работа | Размер: 279.39K | Скачано: 494 | Добавлен 24.05.11 в 12:44 | Рейтинг: +8 | Еще Курсовые работы

Вуз: ВЗФЭИ

Год и город: Барнаул 2011

Содержание

Введение 3

1. Теоретическая часть 4

1.1. Основные понятия. Логические операции 4

1.2. Логические выражения. Порядок логических операций 8

1.3. Основные законы алгебры логики 9

1.4. Табличное и алгебраическое задание булевских функций 10

1.5. Примеры применения алгебры высказываний в информатике 11

Заключение 17

2. Практическая часть 18

2.1. Постановка задачи 18

2.2. Описание алгоритма решения задачи 20

Список литературы 26

Введение

Информатика – прикладная наука, находящаяся на стыке многих наук. Вместе с тем она опирается на спектр разделов такой фундаментальной науки, как математика. Наиболее важное прикладное значение для информатики имеет алгебра высказываний (булева алгебра), названная так по имени  математика Джорджа Буля. Алгебра высказываний используется в разработке алгоритмов программ и в синтезе цифровых устройств, теория множеств и теория графов, используемые в описании различных структур.

Цель данной курсовой работы состоит в изучении применения алгебры высказываний в информатике.

Для достижения цели необходимо выполнить следующие задачи:

- дать основные понятия алгебры высказываний и рассмотреть логические операции;

- выявить порядок логических операций;

- рассмотреть основные законы алгебры логики;

- раскрыть табличное и алгебраическое задание булевских функций.

Для выполнения и оформления курсовой работы был использован компьютер IBM PC совместимый, ЦПУ Intel® Celeron® 2800 МГц, ОЗУ 1.0 Гб с программным обеспечением Microsoft® Windows® XP SP2. 

Практическая часть выполнена с использование пакета MS Excel и MS Word.

1. Теоретическая часть

1.1. Основные понятия. Логические операции

Алгебра высказываний является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний – решение логических задач [6].

Алгебра – это наука, которая изучает множество некоторых элементов и действия (операции) над ними. Если элементы алгебры – натуральные числа, а операции – сложение и умножение, то это алгебра натуральных чисел.

Алгебра высказываний (булева алгебра) названа так по имени  математика Джорджа Буля (1825-1864), внесшего значительный вклад в разработку алгебры логики [7, с 57].

Основное понятие булевой алгебры – высказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать истинно оно или ложно. Восклицательное или вопросительное предложения не являются высказываниями [2, с 2]. Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (0) или ИСТИНА (1). Например, содержание высказывания А: «дважды два равно четырем» истинно А=1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А=В [1, 48].

Логические операции

Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций [4, с 50].

Для установления значений сложных высказываний используют таблицы истинности. Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию, и значениями функции [5, с 267].

С помощью логических операций можно вычислить истинность или ложность некоторого высказывания [3, с 54].

Операцией отрицания А называют высказывание Ā (или ¬А, говорят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то Ā «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание – унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ.

Это правило можно записать в виде следующей таблицы:

А

Ā

0

1

1

0

Такая таблица называется таблицей истинности.

Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается или  (при этом говорят С равно А и В). Примером такой операции может быть следующая: пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери», т.е. данная операция применяется, если два высказывания связываются союзом И.

Таблица истинности этой операции имеет вид:

А

В

А&B

0

0

0

0

1

0

1

0

0

1

1

1

Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается  (при этом говорят: С равно А ИЛИ В). Пример: пусть высказывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе», т.е. данная операция применяется, если два высказывания связываются союзом ИЛИ.

Таблица истинности такой операции следующая:

А

В

0

0

0

0

1

1

1

0

1

1

1

1

Импликацией двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается  (при этом говорят : из А следует В). Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Очевидно, операция не симметрична, т.е. из  не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.

Таблица истинности импликации следующая:

А

В

А→В

0

0

1

0

1

1

1

0

0

1

1

1

Импликация имеет следующие свойства:

А→В≠В→А

A→A=1

0→A=1

1→A=A

A→1=1

A→0= Ā

Эквиваленцией двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается (). Примером такой операции может быть любое высказывание типа: событие А равносильно событию В.

Таблица истинности:

Эквиваленция имеет следующие свойства:

1.2. Логические выражения. Порядок логических операций

С помощью логических операций из простых высказываний можно построить логические выражения, которые также называются булевскими функциями. Например, .

Чтобы избежать большого количества скобок в булевских функциях, принято следующие соглашение о старшинстве операций.

Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция [4, с 52].

В настоящее время существуют достаточно много программных продуктов, с помощью которых можно реализовать различные логические функции. Логические функции широко используются и программе MS Excel. Для вызова необходимо выполнить следующие команды: [Кнопка «Пуск» - Программы – MS Office – Microsoft Excel] и далее команду: [Вставка – Функция]. В открывшемся окне (рис. 1.) «Мастер функций – шаг 1 из 2», выберем «Категория: «Логические» и далее можно выбрать необходимую логическую функцию: ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ. В этом же окне можно получить справку по каждой из этих функций [7, с 63].

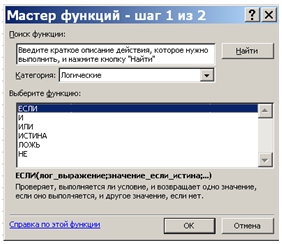
Рис. 1. Диалоговое окно «Мастер функций – шаг 1 из 2»

1.3. Основные законы алгебры логики

В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.

Для простоты записи приведем основные законы алгебры логики для двух логических переменных А и В. Эти законы распространяются и на другие логические переменные [7, с 59].

1. Закон противоречия: ; .

2. Закон исключенного третьего: ; .

3. Закон двойного отрицания: ;  .

4. Законы де Моргана: ; .

5. Законы повторения: ; ; ; .

6. Законы поглощения: ; .

7. Законы исключения констант: ; ; ; ; ; ; ; .

8. Законы склеивания: ; .

9. Законы контрапозиции: .

Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных A, B, C:

1. Коммуникативный закон: ; .

2. Ассоциативный закон: ; .

3. Дистрибутивный закон: .

1.4. Табличное и алгебраическое задание булевских функций

Задать булевскую функцию можно, определяя ее значение для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать  различных наборов. Пусть, например, булевская функция имеет три аргумента: , , . Общее число наборов ; зададим таблицу истинности функции, указав для каждого набора значение функции.

Для составления алгебраической формы по результатам таблицы сделаем следующее. В комбинациях, где функция принимает значение 1, единицу заменим именем функции, а нуль – именем с отрицанием (т.е. комбинации 0 0 1 поставим в соответствие выражение ), все элементы соединим знаками дизъюнкции, для рассматриваемого примера получим .

Построенная функция удовлетворяет заданной таблице истинности. Функция представляет дизъюнктивную нормальную форму (ДНФ). Кроме того, в каждую группу дизъюнкций входят все аргументы функции. Такая ДНФ называется совершенной, а каждая группа дизъюнкции называется конституентой единицы.

Аналогично, для комбинации, где функция принимает значение нуля, можно построить алгебраическую форму , которая также удовлетворяет заданной таблице истинности и представляет собой конъюнктивную нормальную форму, в данном случае совершенную. Каждая конъюнкция называется конституентой нуля [4, с 54-55].

1.5. Примеры применения алгебры высказываний в информатике

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Полусумматор

Cложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором (Рис.1). У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩИЕ ИЛИ и И.

Сумматор

В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа.

Чтобы учесть перенос приходится схему усложнять (Рис. 2). По-сути она получается, состоящей из двух полусумматоров.

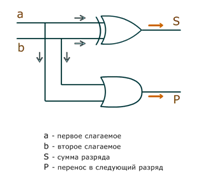
Рис. 1. Схема полусумматора

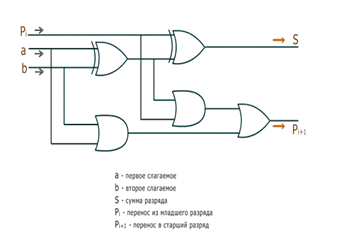
Рис. 2. Схема сумматора

Логические элементы. Вентили

В основе построения компьютеров, а точнее аппаратного обеспечения, лежат так называемые вентили. Они представляют собой достаточно простые элементы, которые можно комбинировать между собой, создавая тем самым различные схемы. Одни схемы подходят для осуществления арифметических операций, а на основе других строят различную память ЭВМ.

Простейший вентиль представляет собой транзисторный инвертор, который преобразует низкое напряжение в высокое или наоборот (высокое в низкое). Это можно представить как преобразование логического нуля в логическую единицу или наоборот, т.е. получаем вентиль НЕ.

Соединив пару транзисторов различным способом, получают вентили ИЛИ-НЕ и И-НЕ. Эти вентили принимают уже не один, а два и более входных сигнала. Выходной сигнал всегда один и зависит от входных сигналов. В случае вентиля ИЛИ-НЕ получить высокое напряжение (логическую единицу) можно только при условии низкого напряжении на всех входах. В случае вентиля И-НЕ все наоборот: логическая единица получается, если все входные сигналы будут нулевыми. Как видно, это обратно таким привычным логическим операциям как И и ИЛИ. Однако обычно используются вентили И-НЕ и ИЛИ-НЕ, т.к. их реализация проще: И-НЕ и ИЛИ-НЕ реализуются двумя транзисторами, тогда как логические И и ИЛИ тремя.

Выходной сигнал вентиля можно выражать как функцию от входных.

Транзистору требуется очень мало времени для переключения из одного состояния в другое (время переключения оценивается в наносекундах). И в этом одно из существенных преимуществ схем, построенных на их основе.

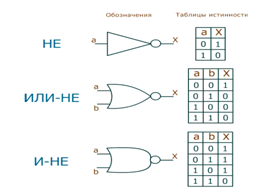
Рис. 3. Основные вентили: НЕ, ИЛИ-НЕ, И-НЕ

Триггер как элемент памяти. Схема RS-триггера

Память (устройство, предназначенное для хранения данных и команд) является важной частью компьютера.

Элементарной единицей компьютерной памяти является бит. Поэтому требуется устройство, способное находиться в двух состояниях, т.е. хранить единицу или ноль. Также это устройство должно уметь быстро переключаться из одного состояния в другое под внешним воздействием, что дает возможность изменять информацию. Ну и наконец, устройство должно позволять определять его состояние, т.е. предоставлять во вне информацию о своем состоянии.

Устройством, способным запоминать, хранить и позволяющим считывать информацию, является триггер.

Разнообразие триггеров весьма велико. Наиболее простой из них так называемый RS-триггер, который собирается из двух вентилей. Обычно используют вентили ИЛИ-НЕ или И-НЕ.

RS-триггер на вентилях ИЛИ-НЕ

RS-триггер «запоминает», на какой его вход подавался сигнал, соответствующий единице, в последний раз. Если сигнал был подан на S-вход, то триггер на выходе постоянно «сообщает», что хранит единицу. Если сигнал, соответствующий единице, подан на R-вход, то триггер на выходе имеет 0. Не смотря на то, что триггер имеет два выхода, имеется в виду выход Q. (Q с чертой всегда имеет противоположное Q значение.)

Другими словами, вход S (set) отвечает за установку триггера в 1, а вход R (reset) – за установку триггера в 0. Установка производится сигналом, с высоким напряжением (соответствует единице). Просто все зависит от того, на какой вход он подается.

Большую часть времени на входы подается сигнал равный 0 (низкое напряжение). При этом триггер сохраняет свое прежнее состояние.

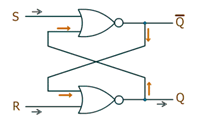
Рис. 4. Схема RS-триггера на вентилях ИЛИ-НЕ

Заключение

В результате работы были выполнены поставленные задачи.

Выявлено основное понятие булевой алгебры – высказывание. Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначается 0) или ИСТИНА (обозначается 1).

Были рассмотрены логические операции: отрицание, конъюнкция, дизъюнкция, импликация и логические выражения, представляющие собой комбинации логических операций.

Был выявлен порядок логических операций. Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.

В результате работы можно выделить основные законы алгебры логики: закон противоречия, закон исключенного третьего, закон двойного отрицания, законы де Моргана, законы повторения, законы поглощения, законы исключения констант, законы склеивания, законы контрапозиции, коммуникативный закон, дистрибутивный закон, ассоциативный закон.

Было раскрыто табличное и алгебраическое задание булевских функций. Задать булевскую функцию можно, определяя ее значение для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать  различных наборов.

Алгебра высказываний является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Одним из приложений алгебры высказываний – решение логических задач. В логических задачах исходными данными являются не только и не столько числа, а сложные логические суждения, подчас весьма запутанные. Эти суждения и связи между ними бывают иногда столь противоречивы, что для их разрешения привлекают вычислительные машины.

2. Практическая часть

2.1. Постановка задачи

В бухгалтерии предприятия ООО «Гамма» производится расчет налоговых вычетов, предоставляемых сотрудникам, и формирование платежных ведомостей. Данные для выполнения расчета налоговых вычетов приведены на рис. 1. Стандартный налоговый вычет предоставляется каждому сотруднику в размере 400 руб. до тех пор, пока совокупный доход с начала года не превысит 50000 руб., налоговый вычет на ребенка предоставляется в размере 600 руб. НДФЛ – налог на доходы физических лиц (13%) рассчитывается с начисленной суммы за минусом размера налогового вычета.

1. Построить таблицы по приведенным ниже данным.

2. Выполнить расчет размера налогового вычета, предоставляемого сотрудникам в текущем месяце, результаты вычислений представить в виде таблицы (рис. 2.).

3. Сформировать и заполнить форму расчетной ведомости по заработной плате за текущий месяц (рис. 3).

4. Результаты расчета заработной платы за текущий месяц представить в графическом виде.

Рис. 1. Данные для расчета налоговых вычетов

Рис. 2. Размер налоговых вычетов, предоставляемых сотрудникам в текущем месяце

Рис. 3. Расчетная ведомость

2.2. Описание алгоритма решения задачи смотрите в файле

Список литературы

1. Андреева Е.В., Фалина И.Н. Системы счисления и компьютерная арифметика: Учебное пособие. М.: БИНОМ. Лаборатория знаний, 2004 – 256с.

2. Булгакова И.Н. Дискретная математика. Элементы теории, задачи и упражнения. Часть 2: Учебное пособие для вузов (2-е издание). - Воронеж: Изд-во ВГУ, 2008. - 76 с.

3. Информатика в экономике: Учеб. пособие /Под ред. проф. Б.Е. Одинцова, проф. А.Н. Романова. – М.: Вузовский учебник, 2008. – 478 с.

4. Информатика: учебник/ Б.В. Соболь – Изд. 3-е, дополн. и перераб. – Ростов н/Д: Феникс, 2007. – 446 с.

5. Роганов Е.А., Тихомиров Н.Б., Шелехов А.М. Математика и информатика для юристов: Учебник. - М.: МГИУ, 2005. - 364 с.

6. Чугайнова А.П. Алгебра высказываний. – http://www.krugosvet.ru (29.03.11.)

7. Яшин В.Н. Информатика: аппаратные средства персонального компьютера: Учеб пособие. - М.: ИНФРА-М, 2008. – 254 с.

24.05.11 в 12:44 Автор:lenka26-18

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Курсовые работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Курсовые работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

Если Курсовая работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

Похожие работы

• Применение алгебры логики в информатике (понятия, формулы)
• Применение алгебры логики в информатике
• Арифметические и логические компьютерные операции