Главная » Бесплатные рефераты » Бесплатные рефераты по математике »
Задача № 04 Найти предел
Тема: Задача № 04 Найти предел
Раздел: Бесплатные рефераты по математике
Тип: Задача | Размер: 44.77K | Скачано: 355 | Добавлен 16.05.17 в 02:05 | Рейтинг: 0 | Еще Задачи
Задача № 04
Найти предел
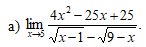
Решение
Функция, предел которой при требуется найти, представляет собой частное двух функций. Однако применить теорему о пределе частного в данном случае нельзя, так как предел функции, стоящей в знаменателе, при ранен нулю.
Преобразуем данную функцию, умножив числитель и знаменатель дроби, находящейся под знаком предела, на выражение (), сопряженное знаменателю. Параллельно разложим квадратный трехчлен в числителе на линейные множители:
4x2-25x+25=0,
D=b2-4ac=(-25)2-4425=625-400=225,
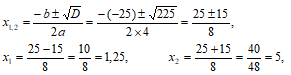
4x2-25x+25=4(x-x1) (x-x2)=4(x-1,25) (x-5)=(x-5)(4x-5).
Получим:
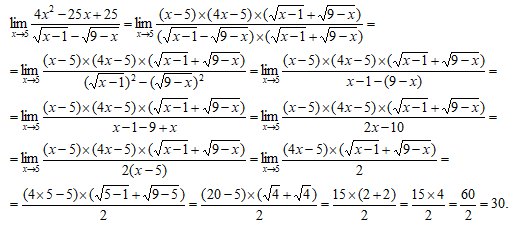
При вычислении мы сократили числитель и знаменатель дроби на общий множитель х – 5 и получили новую функцию, которая отличается от данной значением лишь в одной точке х =5. Исходная функция в этой точке не определена, а новая определена и непрерывна как элементарная функция.
Поскольку переопределение функции в одной точке не сказывается на значении предела и поскольку для функции, непрерывной в точке хо, ее предел при равен значению этой функции в точке х0, то окончательно получили следующее:
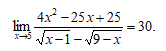
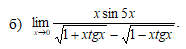
Решение
И в этом примере начнем преобразования с умножения числителя и знаменателя дроби, стоящей под знаком предела, на выражение, сопряженное к знаменателю:
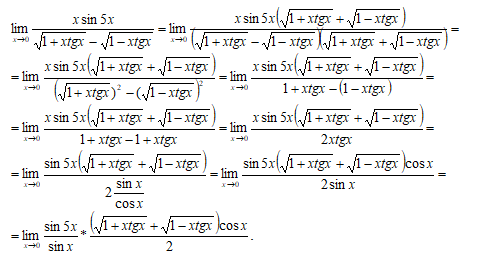
Заметим, что предел в нуле второго сомножителя как непрерывной в нуле функции равен значению функции в этой точке:
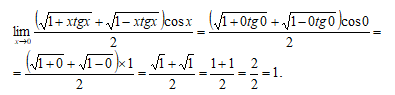
Чтобы найти предел первого сомножителя, разделим его числитель и знаменатель на х:
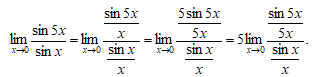
Предел 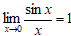 есть первый замечательный предел.
есть первый замечательный предел.
Предел 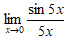 легко сводится к нему:
легко сводится к нему:
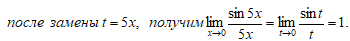
Теперь с помощью теорем о пределе частного и суммы вычисляем предел первого сомножителя:
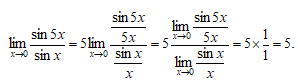
Воспользовавшись, наконец, теоремой о пределе произведения, окончательно получаем:
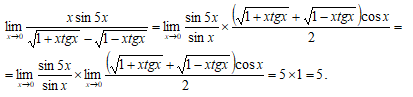
Таким образом,
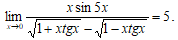
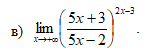
Решение
Прежде всего, преобразуем данную степенно-показательную функцию:
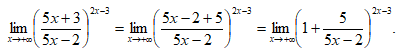
Введем новую переменную
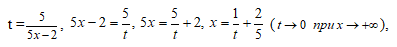
тогда получим следующее:
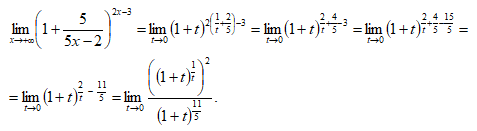
Воспользуемся теоремой о пределе частного и получим:
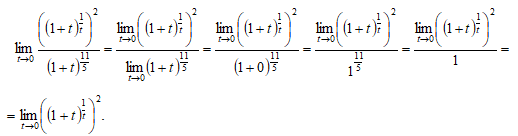
Предел 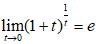 есть второй замечательный предел.
есть второй замечательный предел.
Тогда имеем
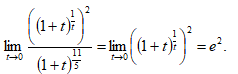
Окончательно получим
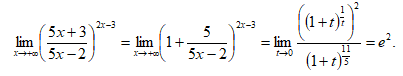
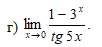
Решение
Представим выражение под знаком предела в виде
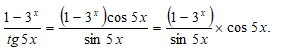
Получим
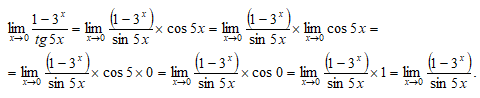
Здесь мы применили теорему о пределе произведения.
Для вычисления предела функции разделим числитель и знаменатель на x и, применяя теорему о пределе частного, первый и второй замечательные пределы и свойство логарифмической функции, получим
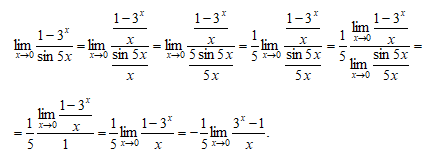
Произведём замену 3x - 1=t, 3x =t+1, x=log3 (t+1). Тогда имеем
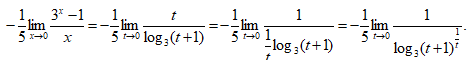
Используя непрерывность логарифмической функции и второй замечательный предел, получим
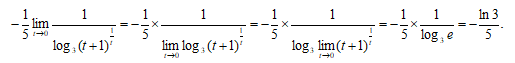
Таким образом, окончательно получим
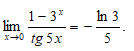
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Задача № 04 Найти предел [16.05.17]](/files/works_screen/3/43/15.png)