Главная » Бесплатные рефераты » Бесплатные рефераты по эконометрике »
Экономический объект - закрытая национальная экономика
Тема: Экономический объект - закрытая национальная экономика
Раздел: Бесплатные рефераты по эконометрике
Тип: Задача | Размер: 20.17K | Скачано: 798 | Добавлен 23.01.17 в 23:50 | Рейтинг: 0 | Еще Задачи
Задача.
Экономический объект - закрытая национальная экономика.
Её состояние в текущем периоде t описывается переменными: Yt – уровень ВВП, Ct – потребление, It – инвестиции, Gt – государственные расходы.
Требуется:
1) Применяя четыре принципа спецификации эконометрических моделей, составить спецификацию макромодели, при составлении которой учесть следующие экономические утверждения:
а) текущее потребление объясняется автономным потреблением и уровнем ВВП в предыдущем периоде, возрастая вместе с ним, но с меньшей скоростью;
б) величина инвестиций прямо пропорциональна приросту ВВП за предшествующий период;
в) государственные расходы возрастают с постоянным темпом роста g;
г) текущее значение ВВП есть сумма текущих уровней потребления, инвестиций и государственных расходов.
2) Представить спецификацию модели в матричном виде, указав вектора yt, xt , вектор случайных возмущений ut , а также матрицы А и В.
3) Преобразовать структурную форму к приведенной форме в развёрнутом и матричном видах, записав вектор случайных возмущений εt и матрицу М.
Решение
Как видим из условия, экзогенные переменные Yt-1, и G объясняют три эндогенных переменных Y, С, I. Тем самым число уравнений в модели должно быть рано трем и это подтверждается экономической теорией. Запишем уравнения в соответствии с приведенными утверждениями экономической теории:
Ct = a0 + al∙Y t-1+ wt,
It = b0+ b1∙Y t-1 + vt,
Yt = Ct + It + Gt,
al>0, bl >0.
Получили структурную запись модели, так как в уравнениях больше чем одна эндогенная переменная.
Представим структурную форму модели в матричном виде. Введем следующие обозначения:
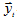 — вектор-столбец текущих значений эндогенных переменных;
— вектор-столбец текущих значений эндогенных переменных;
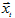 — расширенный вектор-столбец предопределённых переменных, значения которых известны к моменту t;
— расширенный вектор-столбец предопределённых переменных, значения которых известны к моменту t;
А и В — матрицы коэффициентов структурной формы модели (структурные коэффициенты);
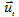 — вектор-столбец текущих возмущений.
— вектор-столбец текущих возмущений.
С учетом данных обозначений матричная запись структурной формы эконометрической модели принимает вид
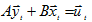
Для этого предварительно в каждом уравнении системы перенесем все члены (кроме случайных возмущений) в левую часть:
Ct – a0 – al∙Y t-1 = wt,
It – b0 – b1∙Y t-1 = vt,
Yt – Ct – It – Gt = 0,
al>0, bl>0.
элементы вектора эндогенных переменных будут следующие:
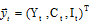
Предопределенные переменные модели — лаговое значение, следовательно, расширенный вектор 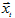 включает три элемента:
включает три элемента:
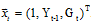
Единичный элемент данного расширенного вектора позволяет учесть наличие свободных членов в поведенческих уравнениях, входящих в систему.
Элементами вектора 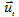 в модели являются текущие возмущения соответствующих поведенческих уравнений и нулевой элемент — правая часть уравнения тождества
в модели являются текущие возмущения соответствующих поведенческих уравнений и нулевой элемент — правая часть уравнения тождества
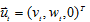
Матрицы структурных коэффициентов А и В состоят из следующих элементов:
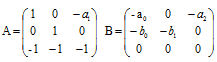
Для преобразования структурной записи модели к приведенной форме правую часть из второго уравнения (I) и правую часть из первого уравнения (С) подставим в третье уравнение и запишем его относительно Yt-1.
Yt = а0 + a1∙Y t-1 + b0 + b2∙ Y t-1 + G
(a1+ b2)∙Y t-1 = а0 + b0 – Yt + G
Y t-1 = (а0 + b0 – Yt + G)/ (a1+ b2)
После того как получена запись решения относительно переменной Yt-1, его правую часть сначала надо подставим в первое уравнение и второе уравнение:
Сt = а0 + a1(а0 + b0 – Yt + G)/ (a1+ b2)
Выполним элементарные алгебраические преобразования:
С = а0 + a1∙ а0/ (a1+ b2) + b0 / (a1+ b2) – Yt /( a1+ b2) + G/( a1+ b2)
I t-1 = b0+ b1∙(а0 + b0 – Yt + G)/ (a1+ b2)
Матричное представление приведённой формы спецификации представлено ниже:
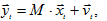
где М – матрица приведенных коэффициентов, которая рассчитывается как
М = -А-1∙В,
Вектор случайных возмущений в приведённой форме получается в результате преобразования
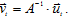
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Экономический объект - закрытая национальная экономика [23.01.17]](/files/works_screen/3/30/22.png)