Логические элементы и их электронные аналоги в компьютере

Тема: Логические элементы и их электронные аналоги в компьютере

Раздел: Бесплатные рефераты по информатике

Тип: Курсовая работа | Размер: 71.45K | Скачано: 210 | Добавлен 10.02.15 в 09:09 | Рейтинг: 0 | Еще Курсовые работы

Оглавление

Введение    2

1. Теоретическая часть. Вариант №10.    3

1.1. Понятие об алгебре высказываний    3

1.2. Основные логические операции    4

1.3. Основные законы алгебры логики    6

1.4. Логические основы ЭВМ    8

2. Практическая часть. Вариант №5.    10

2.1. Постановка задачи    10

2.1.1. Цель решения задачи    10

Произвести расчет стоимости междугородних телефонных разговоров абонента с помощью MS Excel.

2.1.2. Условие задачи    10

2.2. Компьютерная модель решения задачи    12

2.2.1. Информационная модель решения задачи    12

2.2.2. Аналитическая модель решения задачи    13

2.2.3. Технология решения задачи    14

2.3. Результаты компьютерного эксперимента    17

2.3.1. Результаты компьютерного эксперимента    17

2.3.2. Анализ полученных результатов    17

Заключение    18

Список литературы    19

 

Введение

Информатика – прикладная наука, находящаяся на стыке многих наук. Вместе с тем она опирается на спектр разделов такой фундаментальной науки, как математика. Наиболее важное прикладное значение для информатики имеет алгебра высказываний (булева алгебра), названная так по имени  математика Джорджа Буля. Алгебра высказываний используется в разработке алгоритмов программ и в синтезе цифровых устройств.

Тема курсовой работы: Логические элементы и их электронные аналоги в компьютере.

Цель данной курсовой работы состоит в теоретическом изучении логических элементов, реализующих элементарные функции алгебры логики.

Для достижения цели необходимо выполнить следующие задачи:

- дать основные понятия алгебры высказываний;

- рассмотреть логические операции;

- рассмотреть основные законы алгебры логики;

- изучить логические схемы, составленные на основе логических элементов.

 

1. Теоретическая часть. Вариант №10.

1.1. Понятие об алгебре высказываний

Значительный вклад в разработку алгебры логики внес английский математик Джордж Буль (1815-1864). Он создал универсальный логический язык, разработал исчисление высказываний, которое представляет собой формальную логику, переведенную на строгий язык математики. Логика – наука о законах и операциях пра­вильного мышления. Согласно основному принципу логики, пра­вильность рассуждения определяется только его логиче­ской формой, или структурой, и не зависит от конкретного содержания входящих в него утверждений. Различие между формой и содержанием может быть сделано явным с помощью особого язы­к. Отличительная особенность правильного вывода заключается в том, что истинные предпосылки всегда ведут к истинному заключению. Одной из главных задач логики является определить, как прийти к выводу из предпосылок. Логика служит базовым инструментом почти любой науки.

Алгебра высказываний (Булева алгебра) – базовый раздел математической логики, который изучает высказывания или утверждения и операции над ними. Она является системой обозначений, применимой к любым объектам – числам, буквам и предложениям. Пользуясь этой системой, можно закодировать любые утверждения, истинность или ложность которых нужно доказать. Основное понятие булевой алгебры – высказывание – логическое выражение, которое может быть либо истинным, либо ложным. Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначается 0) или ИСТИНА (обозначается 1). Над высказываниями возможны определенные операции. [1, с 105.]

 

1.2. Основные логические операции

Логический элемент — это электронная схема, выполняющая некоторую простейшую логическую операцию. Логический элемент может быть реализован в виде отдельной интегральной схемы. Часто интегральная схема содержит несколько логических элементов. Логические элементы используются в устройствах цифровой электроники для выполнения простого преобразования логических сигналов. Логические (двоичные) элементы служат для выполнения различных логических операций над цифровыми сигналами при двоичном способе их представления. Существенная особенность двоичных цепей в том, что в них рассматриваются не столько величины напряжений, сколько двоичные сигналы. Соответствие между напряжениями и двоичными сигналами устанавливается произвольно. Чаще всего используются дискретные сигналы, нулевому значению которых соответствует уровень низкого электрического потенциала, а единичному значению - уровень высокого потенциала.[2, с 442.]

Из простых логических высказываний образовываются сложные высказывания. Для этого используются союзы: И; ИЛИ; ЕСЛИ…ТО; НЕ. Электронные высказывания обозначают большими буквами латинского алфавита (А, В, С..). В алгебре высказываний определены действия над высказываниями, выполняя которые мы получаем новые высказывания.[3, c 50.]

Объединение двух или нескольких высказываний в одно с помощью союза И называется операцией логического умножения или конъюнкцией. Высказывание А и В истинно тогда и только тогда, когда истинны оба составляющих его высказывания А и В. Возможны различные варианты записи конъюнкции: А˄В = А*В = А&В. Значение истинности логического произведения А ˄ В в зависимости от значений истинности высказываний А и В определяется следующими соотношениями:

0 ˄ 0 = 0; 0 ˄ 1 = 0; 1 ˄ 0 = 0; 1 ˄ 1 = 1.

Объединение двух или нескольких высказываний в одно с помощью союза ИЛИ называется операцией логического сложения или дизъюнкцией. Высказывание А ИЛИ В ложно, тогда и только тогда, когда одновременно ложны высказывания А и В. Дизъюнкцию обозначают: А ˅ В = А + В. Значение истинности логического сложения А ˅ В в зависимости от значений истинности высказываний А и В определяется следующими соотношениями:

0 ˅ 0 = 0; 0 ˅ 1 = 1; 1 ˅ 0 = 1; 1 ˅ 1 = 1.

Операция НЕ называется отрицанием или инверсией и обозначается: Ā = Аʹ. Высказывание НЕ А истинно тогда, когда ложно высказывание А. Значение истинности отрицания высказывания А определяется следующими соотношениями: 1ʹ = 0; 0ʹ = 1.

Эквивалентность (равнозначность) двух высказываний А и В обозначается символом «~». Значение истинности эквивалентных высказываний А и В определяется в зависимости от значений истинности исходных высказываний по следующим соотношениям:

0 ~ 0 = 0; 0 ~ 1 = 1; 1 ~ 0 = 1; 1 ~ 1 = 1.

Операция, при помощи которой высказывания объединяются связкой “ЕСЛИ…, ТО” называется импликацией и обозначается «→». Высказывание А → В ложно тогда, когда А истинно, а В ложно.

Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать любые логические высказывания. [4]

 

1.3. Основные законы алгебры логики

В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.

Наиболее часто применяемые законы алгебры логики:

1).Сочетательный закон (зависимость между двумя высказываниями).

- для конъюнкции:

А ˄ (В ˄ С) = (А ˄ В) ˄ С = А ˄ В ˄ С;

 - для дизъюнкции:

А ˅ (В ˅ С) = (А ˅ В) ˅ С = А ˅ В ˅ С.

2).Переместительный закон (свойство операции не изменять значения при перестановке высказываний).

- для конъюнкции:

А ˄ В = В ˄ А;

 - для дизъюнкции:

А ˅ В = В ˅ А.

3).Распределительный закон.

- для конъюнкции относительно дизъюнкции:

А ˄ (В ˄ С) = (А ˄ В) ˄ (А ˄ С);

 - для дизъюнкции относительно конъюнкции:

А ˅ (В ˅ С) = (А ˅ В) ˅ (А ˅ С).

4).Закон двойственности (инверсии), позволяет заменять отрицание конъюнкции дизъюнкцией отрицаний и наоборот.

(А ˄ В)ʹ = Аʹ ˅ Вʹ;

(А ˅ В)ʹ = Аʹ ˄ Вʹ.

[5, с 59.]

 

1.4. Логические основы ЭВМ

Главной причиной, по которой электронные вычислительные машины (ЭВМ) используют не привычную десятичную, а двоичную систему счисления, является то, что в природе встречается множество явлений с двумя устойчивыми состояниями. Логическими элементами ЭВМ называются технические устройства, осуществляющие элементарные логические операции над входными сигналами. Из простых высказываний можно строить сложные, соединяя простые логическими операции И, ИЛИ, НЕ, называемые соответственно конъюнктор, дизъюнктор и инвертор. Логический элемент имеет один выход, а количество его входов равно числу аргументов логической функции. На основе логических элементов строят более сложные логические схемы – совокупность логических элементов, реализующих какую-либо булеву функцию.

Конъюнктор – логический элемент, реализующий логическую функцию конъюнкции И. Конъюнктор выдает сигнал на выходе при наличии сигнала хотя бы на одном из входов.

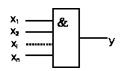
Дизъюнктор – логический элемент, реализующий функцию ИЛИ. Он выдает сигнал на выходе при одновременной подаче сигналов на все его выходы.

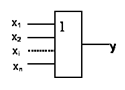
Инвертор реализует функцию НЕ. Различают потенциальные и импульсные инверторы. В потенциальном инверторе высокий уровень входного напряжения преобразуется в низкий и наоборот. В импульсном в момент подачи сигнала на вход появляется сигнал противоположной полярности на его входе.

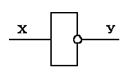
Таким образом, логический элемент – это электронная схема, реализующая элементарную логическую функцию.[1]

 

2. Практическая часть. Вариант №5.

2.1. Постановка задачи

2.1.1. Цель решения задачи

Произвести расчет стоимости междугородних телефонных раз­говоров абонента с помощью MS Excel.

 

2.1.2. Условие задачи

Произвести расчет стоимости междугородних телефонных раз­говоров абонента по заданным значениям. Для определения дня недели, когда производился звонок, следует использовать функцию ДЕНЬНЕД(), а также функции ЕСЛИ() и ИЛИ() (рис. 5.1, рис. 5.2).

Сформировать документ «Квитанция для оплаты телефонных раз­говоров». По данным квитанции построить гистограмму с отраже­нием стоимости звонков на определенную дату.

Тарифы на услуги междугородней телефонной связи ОАО "Россвязь" для абонентов квартирного сектора
Наименование города	Код города	в рабочие дни, руб.	в выходные дни, руб.
Волгоград	8442	4,5	4,2
Киров	8332	4,5	4,2
Пенза	8412	5,5	4,5
Челябинск	3442	7,5	4,8
Новосибирск	3832	7,5	4,8

рис. 5.1.Тарифы на услуги междугородней телефонной связи.

Квитанция для оплаты телефонных разговоров                                           Номер телефона  123-45-67
Дата	Код города	Минут	Стоимость, руб.
15.01.2010	8442	3
16.01.2010	8332	8
17.01.2010	8412	10
18.01.2010	3442	5
23.01.2010	3832	15
Итого
Срок оплаты счета до:

рис. 5.2.Квитанция для оплаты телефонных разговоров.

 

2.2. Компьютерная модель решения задачи

2.2. Компьютерная модель решения задачи

2.2.1. Информационная модель решения задачи

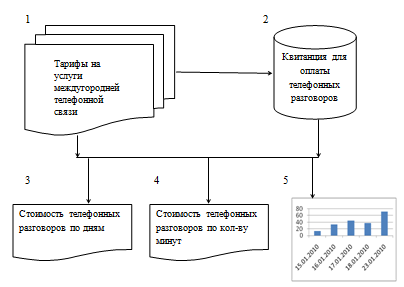
1 – таблица (тарифы на услуги междугородней связи); 2 – документ (квитанция для оплаты телефонных разговоров); 3,4 – таблицы, предназначенные для расчета стоимости; 5 – диаграмма.

 

2.2.2. Аналитическая модель решения задачи

Для получения документа «Квитанция для оплаты телефонных разговоров» необходимо рассчитать следующие показатели:

1. стоимость звонков в зависимости от дня недели;
2. стоимость звонковв зависимости от количества минут разговора;
3. стоимость звонков на определенную дату;
4. общую стоимость телефонных разговоров.

С_v=_gd, =_v,

где – стоимость телефонного разговора; – дата, – код города; С – стоимость звонков на определенную дату; С – общая стоимость.

 

2.2.3. Технология решения задачи

1. Запустить табличный процессор MS Excel.
2. Создать книгу с именем ОАО «Россвязь»
3. Лист 1 переименовать в лист с названием Тарифы.
4. На рабочем листе Тарифы MS Excel создать таблицу «Тарифы на услуги междугородней телефонной связи ОАО «Россвязь» для абонентов квартирного сектора, заполнить ее исходными данными (рис. 5.1).
5. Лист 2 переименовать в лист с названием Квитанция
6. На рабочем листе Квитанция создать таблицу «Квитанция для оплаты телефонных разговоров», в которой будет рассчитана стоимость междугородних телефонных разговоров.
7. Графу Дата в данной таблице заполняем следующим образом:

Занести в ячейку А3 формулу: =ДАТА(2010;1;15)

Занести в ячейку А4 формулу: =ДАТА(2010;1;16)

Занести в ячейку А5 формулу: =ДАТА(2010;1;17)

Занести в ячейку А6 формулу: =ДАТА(2010;1;18)

Занести в ячейку А7 формулу: =ДАТА(2010;1;23)

8. Заполнить таблицу «Квитанция для оплаты телефонных разговоров» исходными данными  (рис. 5.2).
9. На рабочем листе Квитанция MS Excel создаем таблицу «Вспомогательная»
10. Заполняем графу Дата в данной таблице, для определения дня недели:

Занести в ячейку А13 формулу: =ДЕННЕД(А3;2)

Занести в ячейку А14 формулу: =ДЕННЕД(А4;2)

Занести в ячейку А15 формулу: =ДЕННЕД(А5;2)

Занести в ячейку А16 формулу: =ДЕННЕД(А6;2)

Занести в ячейку А17 формулу: =ДЕННЕД(А7;2)

9. После заполнения вспомогательной таблицы приступаем к вычислению Стоимости в таблице «Квитанция для оплаты телефонных разговоров»
10. Заполняем графу Стоимость следующим образом:

Занести в ячейки: 

D3 формулу: =ЕСЛИ(A13=6;D22*C3;C22*C3)*ИЛИ(A13=7;D22*C3;C22*C3)

D4 формулу: =ЕСЛИ(A14=6;D23*C4;C23*C4)*ИЛИ(A14=7;D23*C4;C23*C4)

D5 формулу: =ЕСЛИ(A15=6;C24*C5;D24*C5)*ИЛИ(A15=7;C24*C5;D24*C5)

D6 формулу: =ЕСЛИ(A16=6;D25*C6;C25*C6)*ИЛИ(A16=7;D25*C6;C25*C6)

D7 формулу: =ЕСЛИ(A17=6;D26*C7;C26*C7)*ИЛИ(A17=7;D26*C7;C26*C7)

13. Графу Итого заполняем следующим образом:

Занести в ячейку D8 формулу: =СУММ(D3:D7)

	A	B		C			D
1	Квитанция для оплаты телефонных разговоров Номер телефона 123-45-67
2	Дата	Код города				Минут		Стоимость, руб.
3	15.01.2010	8442				3		13,5
4	16.01.2010	8332				8		33,6
5	17.01.2010	8412				10		45
6	18.01.2010	3442				5		37,5
7	23.01.2010	3832				15		72
8	Итого							201,6
9	Срок оплаты счета до:							25.01.2010
10
11	Вспомогательная
12	Дата	Наименование дня недели
13	5	Пятница
14	6	Суббота
15	7	Воскресенье
16	1	Понедельник
17	6	Суббота
18
19
20	Тарифы на услуги междугородней телефонной связи ОАО "Россвязь" для абонентов квартирного сектора
21	Наименование города	Код города				в рабочие дни, руб.		в выходные дни, руб.
22	Волгоград	8442				4,5		4,2
23	Киров	8332				4,5		4,2
24	Пенза	8412				5,5		4,5
25	Челябинск	3442				7,5		4,8
26	Новосибирск	3832				7,5		4,8

14.Теперь подробно рассматриваем полученные формулы в открытом виде с помощью  функции «Вид формул».

	A		B			C		D
1	Квитанция для оплаты телефонных разговоров Номер телефона 123-45-67
2	Дата			Код города	Минут		Стоимость, руб.
3	=ДАТА(2010;1;15)			8442	3		=ЕСЛИ(A13=6;D22*C3;C22*C3)*ИЛИ(A13=7;D22*C3;C22*C3)
4	=ДАТА(2010;1;16)			8332	8		=ЕСЛИ(A14=6;D23*C4;C23*C4)*ИЛИ(A14=7;D23*C4;C23*C4)
5	=ДАТА(2010;1;17)			8412	10		=ЕСЛИ(A15=6;C24*C5;D24*C5)*ИЛИ(A15=7;C24*C5;D24*C5)
6	=ДАТА(2010;1;18)			3442	5		=ЕСЛИ(A16=6;D25*C6;C25*C6)*ИЛИ(A16=7;D25*C6;C25*C6)
7	=ДАТА(2010;1;23)			3832	15		=ЕСЛИ(A17=6;D26*C7;C26*C7)*ИЛИ(A17=7;D26*C7;C26*C7)
8	Итого						=СУММ(D3:D7)
9	Срок оплаты счета до:						40203
10
11	Вспомогательная
12	Дата			Наименование дня недели
13	=ДЕНЬНЕД(A3;2)			Пятница
14	=ДЕНЬНЕД(A4;2)			Суббота
15	=ДЕНЬНЕД(A5;2)			Воскресенье
16	=ДЕНЬНЕД(A6;2)			Понедельник
17	=ДЕНЬНЕД(A7;2)			Суббота

15. Результаты вычислений представить графически.

 

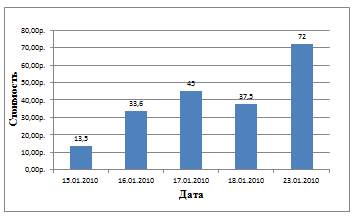
2.3. Результаты компьютерного эксперимента

2.3.1. Результаты компьютерного эксперимента

Дата	Цена за минуту	Всего минут	Стоимость
15.01.2010	4,5	3	4,5*3=13,5
16.01.2010	4,2	8	4,2*8=33,6
17.01.2010	4,5	10	4,5*10=45
18.01.2010	7,5	5	7,5*5=37,5
23.01.2010	4,8	15	4,8*15=72
Всего:			201,6

В результате решения задачи полученные с помощью компьютера ведомости совпадают с текстовыми.

 

2.3.2. Анализ полученных результатов

Таким образом, формирование сводных таблиц на основе «Квитанции для оплаты телефонных разговоров» позволяет решить постав­ленную задачу – произвести расчет стоимости междугородних телефонных раз­говоров абонента. Создание различных диа­грамм на основе данных сводных таблиц средствами MS Excel позволяет наглядно представлять результаты обработки информации для проведения анализа с целью принятия решений.

 

Заключение

В результате работы были выполнены поставленные задачи.

Выявлено основное понятие булевой алгебры – высказывание. Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначается 0) или ИСТИНА (обозначается 1).

Были рассмотрены логические операции: отрицание, конъюнкция, дизъюнкция, импликация, представляющие собой комбинации логических операций.

В результате работы можно выделить основные законы алгебры логики: сочетательный закон, переместительный закон, распределительный закон и закон двойственности.

Алгебра высказываний является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Одним из приложений алгебры высказываний – решение логических задач. В логических задачах исходными данными являются не только и не столько числа, а сложные логические суждения, подчас весьма запутанные. Эти суждения и связи между ними бывают иногда столь противоречивы, что для их разрешения привлекают вычислительные машины.

 

Список литературы

1. Информатика. Теория и практика: учебное пособие / под ред. В.А.Острейковскова, И.В.Полякова – М.: ОНИКС, 2008.

2. Информатика. Под ред. А.В.Могилева, Н.И.Пак – М.: 2008.

3. Информатика: учебник / под ред. Б.В.Соболя: Феникс, 2007.

4. Компьютерная обучающая программа по дисциплине «Информатика» – М.: ВЗФЭИ, 2000. – URL: http://repository.vzfei.ru

5. Информатика: аппаратные средства персонального компьютера: Учебное пособие, Яшин В.Н. – М.: ИНФРА-М, 2008.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Курсовые работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Курсовые работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Курсовая работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---