Контрольная №1, №2, №3 по математике

Тема: Контрольная №1, №2, №3 по математике

Раздел: Бесплатные рефераты по математике

Тип: Контрольная работа | Размер: 68.35K | Скачано: 324 | Добавлен 09.11.14 в 16:16 | Рейтинг: 0 | Еще Контрольные работы

Контрольная работа №1

Задание №1

Найти матрицу, обратную к  матрице.

 

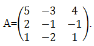
Задание №2

Дана система линейных алгебраических уравнений (СЛАУ)

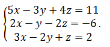
Доказать ее совместимость и решить тремя способами:

1. Методом Гаусса;
2. По формулам Крамера;
3. Средствами матричного исчисления.

 

Задание №3

При каком значении m |a ⃗ |=7, если a ⃗  = mi ⃗ - 6j ⃗ + 2k ⃗?

 

Задание №4

Даны координаты вершин пирамиды А_1 А_2 А_3 А_4

А_1 (14;4;5), А_2 (-5;-3;2), А_3 (-2;-6;-3), А_4 (-2;2;-1). Найти:

1)    Длину ребра  ;   ;    ;

2)    Угол меңду ребрами:   и   ;

3)    Площать грани  ;

4)    Объем пирамиды;

5)    Длину высоты опущенной из вершины    на грань  .

 

Контрольная работа №2

Задание №1.

Составить уравнение плоскости, проходящей через т. М_1(2; 3; -1) и М_2(1; 0; 3), перпендикулярно плоскости 3x – y + 3z + 2 = 6

 

Задание №2.  

В равнобедренном треугольнике АВС заданы вершины С(4; 3), уравнение 2х – у – 5 = 0 основания АС и уравнение х – у = 0 боковой стороны (АВ). Написать уравнение стороны ВС.

 

Задание №3.

Экцентриситст гиперболы √2. Составить каноническое уравнение гиперболы, проходящей через точку М(√3; √2). Построить линию.

 

Задание №4.

Линия задана уравнением r = r(φ) в полярной системе координат, где r ≥ 0. Требуется: 1) построить линию по точкам начиная от     φ = 0 до φ = 2π и придавая φ значение с шагом π/8; 2) найти уравнения данной в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия. Построить линию. R = соsφ – sinφ.

 

Контрольная работа №3

Задание №1.

Найти пределы, не применяя правило Лопиталя.

 

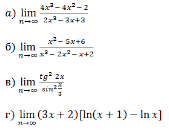
Задание №2.

В пунктах а), б), в), г) найти dx/dx а в пункте д) найти (d^2 x)/(dx^2 )

а) у = ∜(1+tg 6x)
б) у = 〖(〖tg〗^3 x)〗^cos⁡3x
в) y = 〖arccos〗^2 e^(tg 10x)
г) ln(xy) = xy + 28x
д) {█(x= ∛t@y= 1/2  t^2 )┤

 

Задание №3.

Используя геометрический смысл производной (производная равна угловому коэффициенту k = tgα касательной к графику функции f(x) в точке x_0(f´(x_0)=k=tgα)), составить уравнение касательной и нормали к заданной кривой y = f(x) при х = x_0.
у = х/(х^2+ 1) в точке x_0 = -2.

 

Задание №4.

Найти предметы, применяя правило Лопиталя.

〖а) lim┬(n→∞)〗⁡〖lnx/(x-1)〗
〖б) lim┬(n→∞)〗⁡〖(π-2 arctgx)/(ln⁡(1+ 1/x))〗

 

Задание №5.

Исследовать и построить графики следующих функций: у = 〖2х〗^2 – lnx

 

Задание №6.

Найти наибольшее и наименьшее значение функции на отрезке

у = (х-1)/(х+1) +1 при х ∈ [0; 4]

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---