Главная » Бесплатные рефераты » Бесплатные рефераты по методам оптимальных решений »
Методы нелинейной и дискретной оптимизации
Тема: Методы нелинейной и дискретной оптимизации
Раздел: Бесплатные рефераты по методам оптимальных решений
Тип: Контрольная работа | Размер: 451.94K | Скачано: 395 | Добавлен 28.05.14 в 14:35 | Рейтинг: +1 | Еще Контрольные работы
Вуз: Финансовый университет
Содержание:
- Задание 1……………………………………………………………………3
- Задание 2…………………………………………………………………..12
- Задание 3…………………………………………………………………16
- Задание 4…………………………………………………………………..19
- Задание 5……………………………………………………………….….21
Список использованных источников …………………………………………..23
Оценочный лист контрольной работы …………………………………...........24
Задание 1. Методы нелинейной и дискретной оптимизации
Задание 2. Фермер планирует засеять кукурузой и соей 400 га земли. Затраты на сев и уборку кукурузы составят 200 ден. ед./га, сои –100 ден. ед./га. На покрытие расходов, связанных с севом и уборкой урожая, фермер получил кредит в размере 60 тыс. ден. ед. Фермер планирует получить: кукурузы – 30 ц/га, сои – 60 ц/га. Фермер заключил договор на продажу кукурузы по 3 ден. ед./ц и сои по 6 ден. ед./ц. Однако согласно данному договору он обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого – 21 тыс. ц.
Определите, какую площадь нужно засеять фермеру каждой из культур, чтобы получить максимальную прибыль. Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
Решение:
Пусть х1–это количество гектаров кукурузы, которое нужно засеять, а х2–это количество сои. Так как у фермера всего имеется 400 га земли, то первое ограничение задачи имеет вид: х1+ х2 ≤ 400. Найдем общие затраты на сев и уборку кукурузы и сои: (200х1+100х2) ден. ед. Фермер получил на расходы ссуду в 60 тыс. ден., поэтому следующее ограничение имеет вид: 200х1+100х2 ≤ 60 000. Найдем, сколько центнеров зерна соберет фермер: (30х1+60х2) ц. Вместимость склада составляет 21 тыс. центнеров, поэтому следующее ограничение имеет вид: 30х1+60х2 ≤ 21 000. на все переменные наложено ограничение x 1,2 ≥ 0
Построим ЭММ задачи:
max f(X) = 90x1+120x2
х1+ х2 ≤ 400
200х1+100х2 ≤ 60 000
30х1+60х2 ≤ 21 000
x1,2 ≥ 0
Решим задачу графическим методом.
Последнее ограничение означает, что область решений будет лежать в первой четверти декартовой системы координат.
1. Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой x1+x2-400=0. Построим прямую по двум точкам (0;400) и (400;0), которые легко получить в результате последовательного обнуления одной из переменных. На рисунке обозначим ее цифрой I.
Множество решений строгого неравенства — одна из полуплоскостей, на которую делит плоскость построенная прямая. Какая из них является искомой, можно выяснить при помощи одной контрольной точки. Если в произвольно взятой точке, не принадлежащей прямой, неравенство выполняется, то оно выполняется и во всех точках той полуплоскости, которой принадлежит контрольная точка, и не выполняется во всех точках другой полуплоскости. В качестве такой точки удобно брать начало координат. Подставим координаты (0; 0) в неравенство x1+x2-400<0, получим -400 < 0, т.е. оно выполняется. Следовательно, областью решения неравенства служит нижняя полуплоскость.
Аналогичным образом построим области решения двух других неравенств
200x1+100x2=60 000
x1 = 0, x2 = 600
x1 = 300, x2 = 0 (на рисунке прямая II);
30x1+60х2=21 000
x1 = 0, x2 = 350
x1 = 700, x2 = 0 (на рисунке прямая III);
2.Построим вектор целевой функции. Чтобы построить этот вектор, нужно соединить точку (90;120) с началом координат.
3.Приравняем целевую функцию постоянной величине а:
90x1+120x2 = а.
Пусть а=0, 90x1+120x2 = 0. В качестве одной из этих точек удобно взять точку О(0;0), а так как при x1 = 4 x2 = -3, то в качестве второй точки возьмем точку E(4;-3).
Через эти две точки проведем линию уровня f(Х)= 90x1+120x2 = 0.
Получим следующие точки: (0;90) и (120;0).
Построим вектор, координаты которого являются производными функции , т.е. (90;120). Чтобы построить этот вектор нужно соединить (0;0) и (90;120).
Передвигаем линию уровня в направлении вектора, пока она не пересечётся с вершиной области, определяющей самое высокое положение линии уровня.
Вершина В обеспечит максимальное значение функции.
Точка пресечения: х1=100 и х2=300.
В (100;300).
(ден. ед.)
Ответ: Следовательно, чтобы получить максимальную прибыль, фермер должен засеять 100 га земли кукурузой, 300 га – соей. При этом он получит 45 тыс. ден. ед. при реализации зерна по договору.
Если поставить задачу минимизации функции f(Х) = 90x1+120x2 при тех же ограничениях, линию уровня необходимо смещать параллельно самой себе в направлении, противоположном вектору-градиенту. В нашем случае минимум функции будет в точке О (0;0). Это означает, что фермер не получит ни чего, если не засеет поле зерновыми культурами.
Решение задачи в Excel
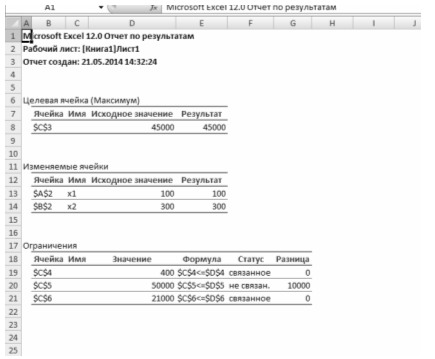
Задание 3. Торговая компания собирается приобрести новый товар – комплекты постельного белья. Ожидаемая потребность – 800 единиц в месяц. Товар можно приобрести у поставщика. Стоимость заказа – 150 руб., годовая стоимость хранения единицы товара –6 руб. Доставка товара осуществляется в течение двух дней. Компания работает 300 дней в году.
Рассчитайте объем заказа, минимизирующий общие годовые расходы компании. Определите:
а) оптимальный объём;
б)годовые расходы на хранение запасов;
в) период поставок;
г) точку заказа.
Решение:
Параметры работы торговой компании: V=800 единиц в месяц, К=150 руб.. h=6 руб., t=2.
Узнаем М=800*12=9600 единиц в год.
Найдем оптимальный объем заказываемой партии , эта формула называется формулой Уилсона.
= = 692,82 комплекты постельного белья нужно заказывать в одну партию.
Найдем годовые издержки хранения запасов:
Z= 150*9600/693+6*693/2=4156 руб./год.
Найдем период доставки:Найдем точку заказа Н=М* t/кол-во дней в году=9600*2/300=64 комплекта постельного белья.Решение задачи в Excel
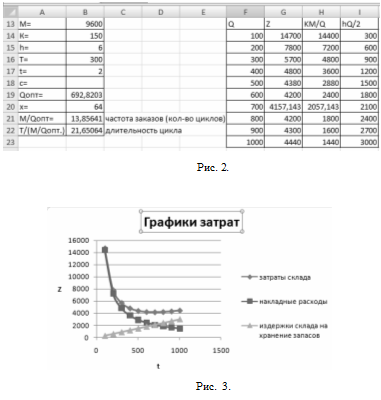
Решение задачи в Excel
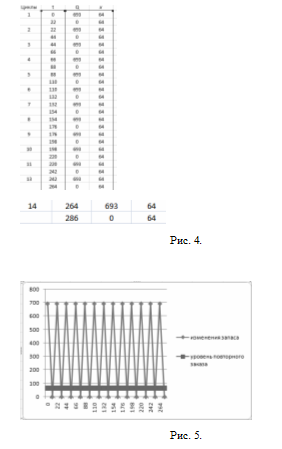
Ответ:
Объем заказа 693 комплекта постельного белья.
а) годовые расходы на хранение запасов 4156 руб./год;
б) период поставок – 22 дня;
в) точку заказа 64 комплекта постельного белья.
Задание 4. В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.) в тот момент, когда оба бухгалтера заняты обслуживанием ранее обратившихся коллег, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно λ=8 , а среднее время, которое затрачивает бухгалтер на оформление документа, – Тср.=7.
Оцените основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Определите, сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%.
Решение:
Рассчитаем μ=1/Tоб=1/7/60==8,57, затем рассчитаем нагрузку на систему α = λ / μ = 8/8,57=0,933
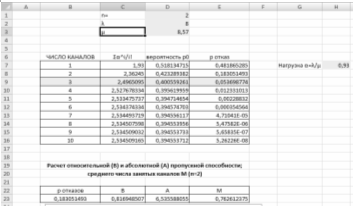
Расчёты проведем в Excel. Видно, что СМО загружена не сильно: из двух бухгалтеров занято в среднем М=0,76, а из обращающихся в бухгалтерию людей около Р отказов=18% остаются незагруженными.
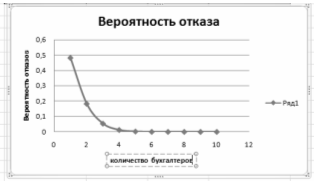
Из графика на рисунке видно , что минимальное число каналов обслуживания (бухгалтеров), при котором вероятность обслуживания работников будет выше 85% (вероятность отказа ниже 15%), равно n=3.
Задание 5. Статистический анализ показал, что случайная величина Х (длительность обслуживания клиента в парикмахерской) следует показательному закону распределения с параметром, а число клиентов, поступающих в единицу времени (случайная величина Y), – закону Пуассона с параметром λ=1,9 и μ=0,6.
Организуйте датчики псевдослучайных чисел для целей статистического моделирования (использования метода Монте-Карло). Получите средствами MS Excel 15 реализаций случайной величины Х и 15 реализаций случайной величины Y.
Решение:
Имитационный эксперимент проведем с использованием MS Excel.
Табличная имитационная модель двухканальной СМО с отказами
На рисунке представлен моделирующий алгоритм (табличная имитационная модель) при числе испытаний N=15.
Для получения случайных чисел с показательным законом распределение Xi=
Случайные числа с равномерным их распределением в интервале от 0 до1 получены с помощью функции =СЛЧИС() Мастер функций (Математические). Эти числа содержатся в ячейках $C$3:$Q$3.
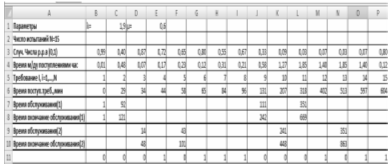
Пятнадцать реализаций с.в. длительность интервала τ (в часах) между очередными поступлениями требований $C$4:$Q$4. Для получения, содержимого ячейки С4 использовать функции = (-1/C1)*LN(B3).
Соответственно, кумулятивным образом (строка 6) на временной оси [0, Т] зафиксировано время Тi (i=1,2,…,15) поступления требований (в минутах, с округлением).
Для получения реализаций с.в. длительности обслуживания t (в минутах, с округлением) в соответствующую ячейку электронной таблицы (строки 7 и 9) записывается формула =60*(-1/6)*LN(СЛЧИС()).
Далее последовательно сравниваются время окончания обслуживания каналами (строки 8 и 10) и время поступлениями требований (строка 6); соответственно, в счётчике отказов (строка 11) фиксируется 0 (требование принято к обслуживанию) или 1(требованию отказано в обслуживании).
В соответствии со счётчиком отказов (в ячейках $C$12:$Q$12) зафиксировано 7 отказов, т.е. статистическая оценка вероятности отказа в данной СМО при N=15 равна (7/15)=0,47.
Список использованных источников
- Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие. – М.: Вузовский учебник, 2012.
- Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2е изд., испр. и доп. –М.: Вузовский учебник : ИНФРА-М, 2012.
- Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: учебное пособие. –М.: Вузовский учебник, 2012.
- Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров. –3 изд., перераб. и доп. – М.: Юрайт, 2012.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Методы нелинейной и дискретной оптимизации [28.05.14]](/files/works_screen/1/70/73.png)