Лабораторная работа по Методам оптимальных решений Вариант №7

Тема: Лабораторная работа по Методам оптимальных решений Вариант №7

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Лабораторная работа | Размер: 1.15M | Скачано: 263 | Добавлен 22.05.14 в 14:04 | Рейтинг: 0 | Еще Лабораторные работы

Вуз: не указан

Задача 1.

1. Составим экономико-математическую модель задачи.

Введем обозначения:

x₁ – количество фруктов (г);

x₂ – количество овощей (г);

x₃ – количество рыбы (г);

x₄ – количество крупы (г);

x₅ – количество мясо (г);

x₆ – количество сахара (г).

X = (x₁, x₂, x₃, x₄, x₅, x₆) – искомый дневной рацион.

Составим целевую функцию, значение которой является суммарная калорийность рациона:

F(X) = 400x₁ + 300x₂ + 800x₃ + 3200x₄ + 1500x₅+ 3500x₆

Тогда экономико-математическая модель задачи примет следующий вид:

Найти минимум функции  F(X) = 400x₁ + 300x₂ + 800x₃ + 3200x₄ + 1500x₅+ 3500x₆

при выполнении системы ограничений

0,007x₁+0,02x₂+0,15x₃+0,12x₄+0,2x₅+0,003x₆ ≥ 100

0,001x₂+0,1x₃+0,02x₄+0,1x₅ ≤ 75

0,2x₁+0,1x₂+0,75x₄+0,95x₆ ≥ 500

x_i ≥ 0  (i=1,2,3,4,5,6)

2. Решим полученную задачу линейного программирования с помощью надстройки «Поиск решения»

Создадим форму для ввода условий задачи и введем зависимости для целевой функции, зависимости для левых частей ограничений:

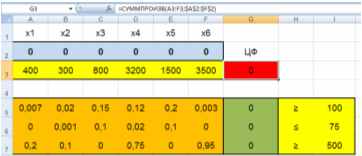
Рис. 1. Форма для ввода условий задачи в расчетном виде

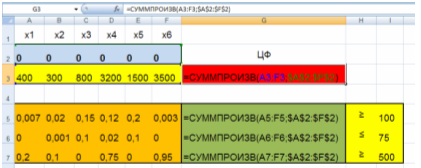
Рис. 2. Форма для ввода условий задачи в формульном виде

Заполним поля диалогового окна Поиск решения (целевая ячейка, направление целевой функции, изменяемые ячейки, ограничения), зададим параметры для решения ЗЛП:

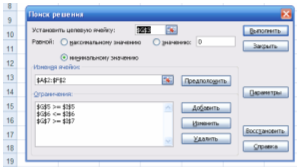
Рис. 3. Диалоговое окно Поиска решения

Нажимаем выполнить, предварительно установив в разделе ПАРАМЕРЫ отметку НЕОТРИЦАТЕЛЬНЫЕ, получим:

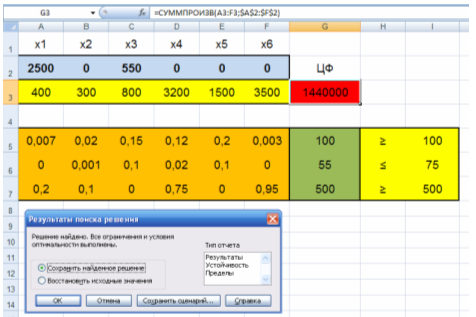
Рис. 4. Решение задачи с помощью надстройки Поиск решения

Ответ:

Таким образом, для получения пищи с минимальным количеством калорий в количестве 1440000 кал/г в рацион питания необходимо включить

- фрукты в количестве 2500 г.

- рыбу в количестве 550 г.

 

Задача 2.

1. Составим экономико-математическую модель задачи.

Введем обозначения:

xij – количество единиц работы, выполненной механизмом вида ai, на участке работы bj. Требуется определить план распределения механизмов, максимизирующей целевую функцию (выражающую суммарную производительность всех механизмов при выполнении всех видов работ):

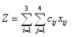
при ограничениях:

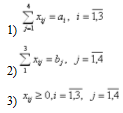
- все механизмы должны быть задействованы;
- все учас  тки должны быть загружены;
- количество единиц работы не может быть отрицательным

Тогда целевая функция задачи будет представлена формулой (1), ограничения к ней – формулами (2).

Z(Х) = 3x₁₁+2x₁₂+x₁₃+0x₁₄+

         +2x₂₁+5x₂₂+3x₂₃+4x₂₄+

         +x₃₁+0x₃₂+4x₃₃+ 2x₃₄        →   max

x₁₁+x₂₁+x₃₁=10,

x₁₂+x₂₂+x₃₂=20,

x₁₃+x₂₃+x₃₃=30

x₁₄+x₂₄+x₃₄=40

x₁₁+x₁₂+x₁₃+x₁₄=45

x₂₁+x₂₂+x₂₃+x₂₄=20

x₃₁+x₃₂+x₃₃+x₃₄=35

x_ij - целые

x_ij≥0  (i=1,2,3; j=1,2,3,4)

2. Решим полученную задачу линейного программирования с помощью надстройки «Поиск решения»

Создадим форму для ввода условий задачи и введем зависимости для целевой функции, зависимости для левых частей ограничений:

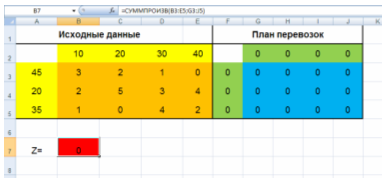
Рис. 1. Форма для ввода условий задачи в расчетном виде

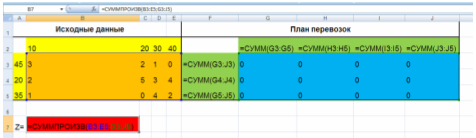
Рис. 2. Форма для ввода условий задачи в формульном виде

Заполним поля диалогового окна Поиск решения (целевая ячейка, направление целевой функции, изменяемые ячейки, ограничения), зададим параметры для решения ЗЛП:

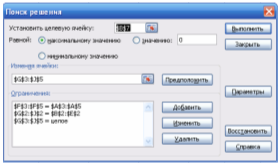
Рис. 3. Диалоговое окно Поиска решения

Нажимаем выполнить, предварительно установив в разделе ПАРАМЕРЫ отметку НЕОТРИЦАТЕЛЬНЫЕ, получим:

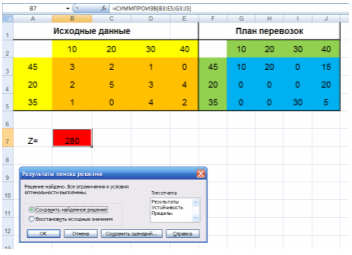
Рис. 4. Решение задачи с помощью надстройки Поиск решения

Ответ:

Таким образом, максимум целевой функции (максимальная суммарная производительность) составит 280 и при этом необходимо:

- 1-ый механизм закрепить за участком 1 в количестве 10 шт, за участком 2 в количестве 20 шт и за участком 4 в количестве 15 шт

- 2-ой механизм закрепить за участком 4 в количестве 20 шт, то есть все механизмы закрепить за участком 4

- 3-ий механизм закрепить за участком 3 в количестве 30 шт и за участком 4 в количестве 5 шт.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Лабораторные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Лабораторные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Лабораторная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---