Лабораторные работы по Методам оптимальных решений

Тема: Лабораторные работы по Методам оптимальных решений

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Лабораторная работа | Размер: 1.98M | Скачано: 446 | Добавлен 20.10.13 в 15:22 | Рейтинг: 0 | Еще Лабораторные работы

Вуз: не указан

Лабораторная работа № 1

 Задание. Фабрика выпускает три вида тканей, причем суточное плановое задание составляет: не менее 90 м ткани I вида, 70 м — II вида и 60 м — III вида. Суточные ресурсы следующие: 780 ед. производственного оборудования, 850 ед. сырья и 790 ед. электроэнергии, расход которых на 1 м ткани представлен в таблице. Цена 1 м ткани I вида равна 80 ден. ед., II вида — 70 ден. ед., III вида — 60 ден. ед.

Ресурс	Расход ресурса на 1 м. ткани вида
	I	II	III
Оборудование	2	3	4
Сырье	1	4	5
Электроэнергия	3	4	2

Требуется определить:

1) сколько метров тканей каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной;

2) какие виды тканей невыгодны предприятию;

3) как изменится общая стоимость продукции и план ее выпуска, если запасы дефицитных ресурсов увеличить на 5%?

Решение:

Обозначим через Х₁, Х₂, Х₃ виды ткани

Целевая функция – выражение, которое необходимо максимизировать:

80Х1 + 70Х2 + 60Х3®max

Ограничения по ресурсам:

2Х₁ + 3Х₂ + 4Х₃ ≤ 780

1Х₁ + 4Х₂ + 5Х₃ ≤ 850

3Х₁ + 4Х₂ + 2Х₃ ≤ 790

Х₁≥90, Х₂≥70, Х₃≥60

Вводим данные и формулы в рабочий лист MC Excel

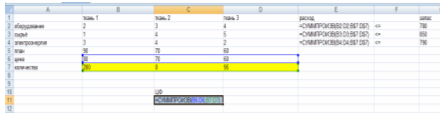
Рисунок 1. Исходные данные и формулы на листе MC Excel

В меню Сервис Поиск решения указываем ограничения. Для ввода ограничений используем кнопку Добавить.

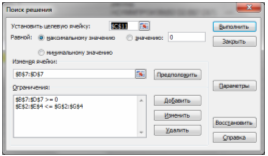
Рисунок 2. Диалоговое окно «Поиск решения» для указания ограничений.

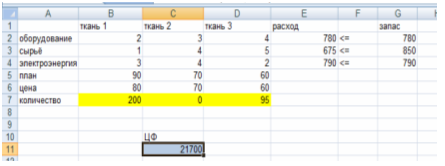
Рисунок 3. Результат

Если запасы дефицитных ресурсов увеличить на 5%, то общая стоимость продукции и план ее выпуска составляет:

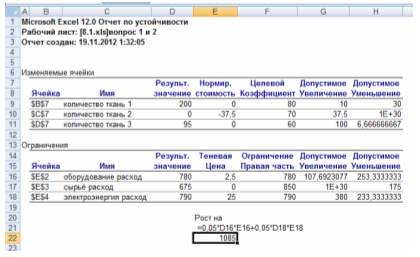
Рисунок 4. Отчет по устойчивости

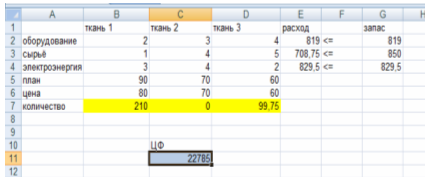
Рисунок 5. Увеличение запасов дефицитных ресурсов на 5%.

Лабораторная работа №2

Задание. Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить работы на пяти участках автодорог. Песок на эти участки можно доставлять из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны также месячные объемы потребностей по участкам работ. Экономические оценки транспортных затрат (в ден. ед.) на перевозку 1 т песка с карьеров на ремонтные участки содержатся ниже в матрице планирования:

Участок работ Карьер	В1	В2	В3	В4	В5	Предложение, т
А1	5	3	4	6	4	40
А2	3	4	10	5	7	20
А3	4	6	9	3	4	40
Потребности, т	25	10	20	30	15

1. Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.

2. Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от карьера А3 до участка работ B4; б) по этой коммуникации будет ограничен объем перевозок — 5 т?

Решение:

Задача относится к закрытому виду, т.к. предложение (40+20+40)=100 равно потребности (25+10+20+30+15)=100.

Обозначим через Х_ij объем перевозок с i-го карьера в j-й участок работ.

Целевая функция – выражение, которое необходимо минимизировать:

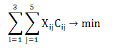
Ограничения:

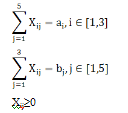
Вводим данные и формулы в рабочий лист MC Excel

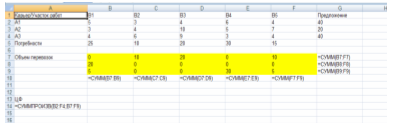
Рисунок 1. Исходные данные и формулы на листе MC Excel

В меню Сервис Поиск решения указываем ограничения. Для ввода ограничений используем кнопку Добавить.

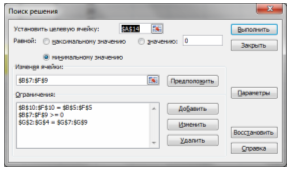
Рисунок 2. Диалоговое окно «Поиск решения» для указания ограничений

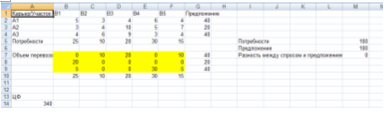
Рисунок 3. Результат

Данный план перевозок показывает, каким образом нужно распределить песок из каждого карьера по участкам, чтобы обеспечить минимальные совокупные транспортные издержки.

Запрет перевозки от карьера А3 до участка работ B4 производим с помощью ограничения:

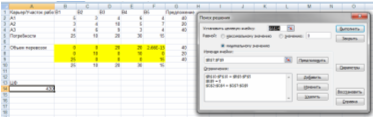
Рисунок 4. Запрет

При запрете перевозки изменяется распределение песка по участкам работ и, соответственно, меняется целевая функция.

Ограничение перевозки от карьера А3 до участка работ B4 производим с помощью ограничения:

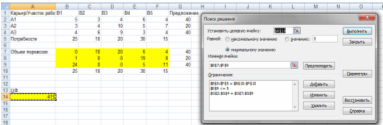
Рисунок 5. Ограничение

При ограничении перевозки от карьера А3 до участка В4 меняется распределение песка по участкам и, соответственно, меняется целевая функция.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Лабораторные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Лабораторные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Лабораторная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---