Главная » Бесплатные рефераты » Бесплатные рефераты по методам оптимальных решений »
Принцип оптимальности, общая задача оптимального программирования
Тема: Принцип оптимальности, общая задача оптимального программирования
Раздел: Бесплатные рефераты по методам оптимальных решений
Тип: Контрольная работа | Размер: 1.00M | Скачано: 609 | Добавлен 22.05.13 в 14:52 | Рейтинг: +5 | Еще Контрольные работы
Вуз: Финансовый университет
План.
1. Принцип оптимальности, общая задача оптимального программирования. Получение оптимальных решений средствами MS Excel 3
2. Задача 2 11
3. Задача 3 17
4. Задача 4 19
5. Задача 5 23
1. Принцип оптимальности, общая задача оптимального программирования. Получениеоптимальных решений средствами MS Excel.
Линейное программирование — это частный раздел оптимального программирования. В свою очередь оптимальное (математическое) программирование — раздел прикладной математики, изучающий задачи условной оптимизации. В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении.
Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Именно такие ситуации, как правило, и составляют повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и т. д.).
Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение (x1, x2,…, xn), где xj , (j = )— его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
Слова «наилучшим образом» здесь означают выбор некоторого критерия оптимальности, т. е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум рентабельности» и др.
Слова «учитывало бы внутренние возможности и внешние условия производственной деятельности» означают, что на выбор планово-управленческого решения (поведения) накладывается ряд условий, т. е. выбор осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
Таким образом, реализовать на практике принцип оптимальности в планировании и управлении — это значит решить экстремальную задачу вида:
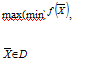
Где — математическая запись критерия оптимальности — целевая функция. Задачу условной оптимизации (1.1), (1.2) обычно записывают в виде:
Найти максимум или минимум функции
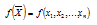
При ограничениях
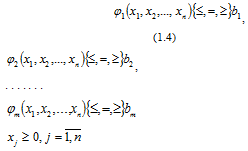
Условие (1.5) необязательно, но его всегда при необходимости можно добиться. Обозначение говорит о том,
Что в конкретном ограничении возможен один из знаков: или . Более компактная запись:
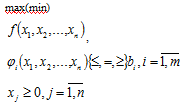
Задача (1.6)-(1.8) — общая задача оптимального (математического) программирования, иначе — математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности и системности.
Вектор X (набор управляющих переменных ) называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А тот план (допустимое решение), который доставляет максимум или минимум целевой функции , называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными —
а) линейные,
б) нелинейные.
В случае а) все функциональные связи в системе ограничений и функция цели — линейные функции; наличие нелинейности хотя бы в одном из упомянутых элементов приводит к случаю б).
2. По характеру изменения переменных —
а) непрерывные,
б) дискретные.
В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения.
3. По учету фактора времени —
а) статические,
б) динамические.
В задачах а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае б) такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени.
4. По наличию информации о переменных —
а) задачи в условиях полной определенности (детерминированные),
б) задачи в условиях неполной информации,
в) задачи в условиях неопределенности.
В задачах б) отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения. В случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.
5. По числу критериев оценки альтернатив —
а) простые, однокритериальные задачи,
б) сложные, многокритериальные задачи.
В задачах а) экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному;
Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а)2а)3а)4а)5а) — задачи и методы линейного программирования, 1б)2а)3а) 4а)5а) — задачи и методы нелинейного программирования, 1а)2б)3а)4а)5а) — задачи и методы целочисленного (дискретного) линейного программирования и т. д.
Получение оптимальных решений средствами MS Excel.
Компания Frontline Systems разработала несколько версий программы поиска оптимальных решений Solver для фирмы Microsoft, одна из которых поставляется вместе с программой Excel. Надстройка Solver в русской версии Excel называется Поиск решения. Кроме того, Frontline Systems разработала несколько расширенных коммерческих программ-оптимизаторов, в том числе надстройку Premium Edition Solver — более расширенную версию программы поиска оптимальных решений по сравнению с надстройкой Поиск решения.
Перед проведением оптимизации надстройку Поиск решения необходимо активизировать (через основное меню Сервис/Надстройки или через Офис (кнопка)/Параметры/Надстройки в Excel.
Рассмотрим реализацию оптимизационной ЭММ средствами надстройки Поиск решения.
Первым этапом при работе с надстройкой (основное меню
Сервис/Поиск решения или Данные/Поиск решения в Excel) является создание специализированного (рабочего) листа, т.е. специальная запись ЭММ в терминах электронной таблицы (ЭТ) Excel (иногда говорят о формировании табличной модели на рабочем листе Excel).
Для этого необходимо определить в ЭТ целевую ячейку, в которой записывается целевая функция модели, а также одну или несколько изменяемых (переменных) ячеек, которые, как правило, отвечают основным переменным в модели и значения которых могут изменяться для достижения экстремума (максимума или минимума) целевой функции. Для успешного поиска решения необходимо, чтобы каждая из переменных ячеек (в общем случае можно задать до двухсот таких ячеек) влияла на целевую ячейку. Другими словами, формула в целевой ячейке должна опираться в вычислениях на значения переменных ячеек. В противном случае при выполнении команды Поиск решения появляется сообщение об ошибке Результаты целевой ячейки не сходятся.
Ограничения модели определяются с помощью значений соответствующих ячеек-функций, которые должны находиться в определенных пределах или удовлетворять граничным условиям. Ограничения могут налагаться как на целевую, так и на переменные ячейки (по два ограничения для каждой изменяемой ячейки с указанием верхнего и нижнего пределов, а также до ста дополнительных).
Таким образом, на специализированном листе должны содержаться ячейки (ячейки-функции), в которых вычисляются ограничиваемые величины.
После оформления рабочего листа переходят ко второму этапу — оформлению диалогового окна Поиск решения, которое появляется после выполнения команды Сервис (основное меню)/Поиск решения или Данные (основное меню)/Поиск решения. Тип каждого из ограничений модели ( ) задается (вводится) в специальном окне Ограничения диалогового окна Поиск решения. Численные значения самих ограничений включать в специализированный лист необязательно — они могут вводиться в специальном окне Ограничения диалогового окна Поиск решения.
Для большинства небольших моделей очень редко возникает необходимость в изменении установленных по умолчанию параметров специального окна Параметры диалогового окна Поиск решения (исключение составляют параметры Линейная модель и Неотрицательные значения). Общая информация, касающаяся установки параметров специального окна Параметры поиска решения, может быть получена в режиме Справка этого окна.
На третьем этапе происходит анализ результатов оптимизации. После команды Выполнить диалогового окна Поиск решения осуществляется поиск оптимального решения — в итоге появляется диалоговое окно Результаты поиска решения.
При использовании режима Справка диалогового окна Результаты поиска решения можно получить сведения об итоговых сообщениях процедуры поиска решения.
При успешном завершении решения задачи в диалоговом окне Результат поиска решения появляется сообщение Решение найдено.
С помощью рубрики Результаты этого диалогового окна можно получить отчет по результатам решения. Рубрики Устойчивость и Пределы позволяют провести дополнительный экономико-математический анализ оптимального плана и получить отчеты по устойчивости и по пределам.
О неудачном завершении работы можно узнать, используя режим Справка в диалоговом окне Поиск решения:
• если система ограничений несовместна, Excel будет выдавать
сообщение Поиск не может найти подходящего решения;
• если решение задачи отсутствует, так как целевая функция не ограничена на множестве допустимых решений, Excel будет выдавать сообщение Значения целевой ячейки не сходятся.
Сообщение Решение найдено означает, что получено оптимальное решение. Однако возможно, что есть другие решения с тем же самым значением ЦФ, т.е. другие альтернативные оптимальные решения (случай неединственности решения).
Если решение не вырождено и модель линейна, то о существовании альтернативных оптимальных решений сигнализируют нулевые значения в столбцах Допустимое увеличение или Допустимое уменьшение
для некоторых переменных решения в Отчете по устойчивости, формируемом надстройкой Поиск решения. Другой информации об альтернативных оптимальных решениях в Отчете по устойчивости нет.
Необходим повторный запуск программы Поиск решения с немного отличающимися значениями переменных решения для нахождения другого оптимума.
Для нелинейной модели сообщение Решение найдено означает, что получен локальный оптимум или при наличии у задачи соответствующих свойств — глобальный оптимум. Из отчетов программы Поиск решения невозможно узнать, локальным или глобальным
оптимумом является решение и есть ли альтернативные оптимумы.
Единственный способ обнаружить другие оптимумы — процесс многократной оптимизации с помощью некоторой систематической стратегии перебора начальных значений переменных задачи.
Задание 2. Решить графическим методом типовую задачу оптимизации. Осуществить проверку правильности решения с помощью средств MS Excel (надстройки Поиск решения).
Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено на сумму по крайней мере в два раза большую, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.
Дивиденды по акциям А составляют 8% в год, по акциям В — 10%. Какую максимальную прибыль можно получить в первый год?
Построить экономико–математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решить задачу на минимум, и почему?
Задание 3. Рассчитать параметры моделей экономически выгодных размеров заказываемых партий.
Предприятие ежегодно закупает 15000 зеркал размером 4х1500х2000 мм и использует их для сборки мебели. Затраты на хранение одного зеркала в течение года составляют 25 руб./шт. Затраты на осуществление заказа – 1800 руб. Предприятие работает 300 дней в году. Доставка заказа от поставщика осуществляется в течении четырех рабочих дней.
Определите:
а) оптимальный объем заказа,
б) период поставок,
в) точку заказа,
г)затраты на управление запасами за год.
Задание 4. Использовать методы теории массового обслуживания для исследования предлагаемой хозяйственной ситуации. При моделировании предполагается, что поток требований на обслуживание является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному (показательному) закону. Задачу следует решить с помощью средств MS Excel.
В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.), когда оба бухгалтера заняты обслуживанием ранее обратившихся работников, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно l; среднее время, которое затрачивает бухгалтер на оформление документа, равно Тср мин. (значения l и Тср по вариантам даны ниже в таблице).
Оценить основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%?
|
№ варианта, задачи |
Параметр l |
Параметр Тср=1/μ |
|
4.1 |
18 |
10 |
Задание 5. Организуйте датчики псевдослучайных чисел для целей статистического моделирования (для использования метода Монте-Карло).
Статистический анализ показал, что случайная величина Х длительности обслуживания клиента в парикмахерской следует показательному закону распределения с параметром μ, а число поступающих в единицу времени клиентов (с.в. У) - закону Пуассона с параметром l . Значения параметров l и μ повариантно даны ниже в таблице.
Получите средствами MS Excel 15 реализаций с.в. Х и 15 реализаций с.в. У.
|
№ варианта, задачи |
Параметр l |
Параметр μ |
|
5.2 |
1,6 |
0,3 |
Чтобы полностью ознакомиться с контрольной, скачайте файл!
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Принцип оптимальности, общая задача оптимального программирования [22.05.13]](/files/works_screen/1/45/8.png)