Пределы

Тема: Пределы

Раздел: Бесплатные рефераты по математическому анализу и линейной алгебре

Тип: Шпаргалка | Размер: 14.47K | Скачано: 1430 | Добавлен 10.10.10 в 09:41 | Рейтинг: +2 | Еще Шпаргалки

Пределы

Основные понятия и определения

Определение: Функция 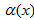 бесконечно малой величиной (БМВ) при  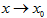или при 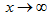, если ее предел равен нулю:

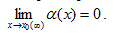
Свойства бесконечно малых величин:

-    алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;

-    произведение БМВ на ограниченную функцию есть БМВ;

-    частное от деления БМВ на функцию, предел которой отличен от 0, есть БМВ.

Определение: Функция b(x) называется бесконечно большой величиной (ББВ) при 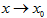  или при  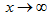, если ее предел равен бесконечности.

!!! Если a(x) - БМВ при 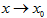или при  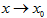, то функция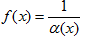 

является ББВ при 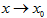 или при  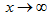 . Верно и обратное утверждение.

Свойства бесконечно больших величин:

-    сумма ББВ и ограниченной функции, есть ББВ;

-    произведение ББВ на функцию, предел которой отличен от 0 есть ББВ;

-    частное от деления ББВ на функцию, имеющую предел, есть ББВ.

 

Основные теоремы о пределах

1.    Функция не может иметь более одного предела.

2.    Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций.

3.    Предел произведения конечного числа функций равен произведению пределов этих функций.

4.    Предел постоянной величины равен этой постоянной.

5.    Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен 0).

6. Формулы: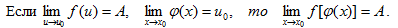 

Виды неопределенностей

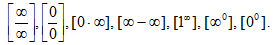
!!! Основной задачей при вычислении пределов является устранение неопределенностей с помощью алгебраических преобразований.

1)    для неопределенности вида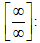 

-    Если в числителе и знаменателе сложные степенные или показательные функции и  . Вычисление пределов в случае отношения степенных функций производится путем вынесения за скобку в числителе и знаменателе дроби переменной x в наибольшей степени среди всех слагаемых дроби (неопределенность устраняется после сокращения дроби и применения основных теорем о пределах); в случае показательных функций за скобку выносится наибольшее слагаемое.

-    Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле, т.е.

 

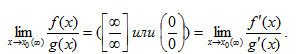
Чтобы полностью ознакомиться с пределами, скачайте файл!

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Шпаргалки на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Шпаргалки для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Шпаргалка, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---