Тема: Лабораторная работа №1, 2, 3 по эконометрике

Раздел: Бесплатные рефераты по эконометрике

Тип: Лабораторная работа | Размер: 697.69K | Скачано: 427 | Добавлен 16.04.09 в 09:10 | Рейтинг: +13 | Еще Лабораторные работы

Вуз: ВЗФЭИ

Год и город: Уфа 2009

ЛАБОРАТОРНАЯ РАБОТА №1

Множественная регрессия

Порядок  выполнения.

1. Импортируем данные из файла формата Excel в SPSS. После запуска программы SPSS выберем в строке меню Файл – Открыть - Данные. Зададим имя Excel, его тип, затем нажмем кнопку OPEN.

В новом диалоговом окне зададим диапазон ячеек … .

На экране появляются импортированные данные в формате SPSS.

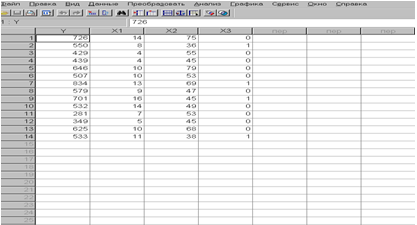
Рис.1.1 Данные задачи представлены в формате SPSS

Редактируем данные с помощью пакета SPSS.

Для этого нажмем в нижней строке меню кнопку «переменные». Это позволит просмотреть всю информацию о переменных, импортированных в SPSS-файл, и внести нужные изменения. В столбце «Метка» введем расширенное имя  переменной. Эта информация будет использована для отчетов.

Используя меню Файл – Сохранить как – Save, сохраним данный файл с расширением .sav.

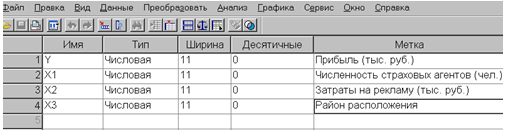
Рис. 1.2. Редактирование данных SPSS

 

2. Выбор факторных признаков для построения регрессионной модели на основе анализа матрицы коэффициентов корреляции.

Для построения матрицы парной корреляции всех переменных с помощью пакета SPSS выполним следующие действия:

Выберем в верхней строке меню Анализ – Корреляция – Парные.

Переменные, относительно которых проверяется степень корреляционной связи, поочередно поместим в поле тестируемых переменных справа.

Начнем расчет путем нажатия ОК.

В результате в выходной области появилась матрица парной корреляции всех переменных. Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т. е. прибыль, имеет тесную связь с районом расположения.

На основе анализа матрицы коэффициентов парной корреляции делаем вывод о целесообразности построения двухфакторного регрессионного уравнения Y=f(X2,X5).

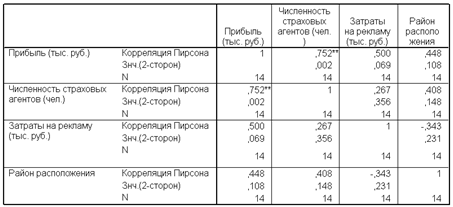
Рис 1.3. Матрица парной корреляции всех переменных

 

3. Построение линейного уравнения регрессии

Для проведения регрессионного анализа с помощью пакета SPSS выполним следующие действия:

Выберем в верхней строке меню Анализ – Регрессия – Линейная.

Поместим переменную Y в поле для зависимых переменных, объявив переменные X1,, X2, X4, X5 независимыми.

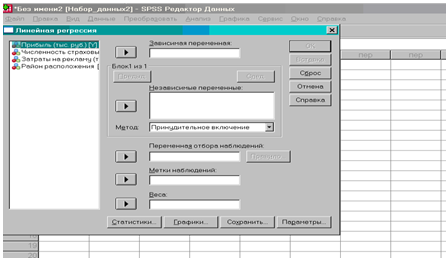
Рис 1.4. Диалоговое окно Линейная регрессия

В полях панели Статистика отметим флажками Оценки, Согласие модели и критерий Дурбина-Уотсона, затем нажмем Продолжить.

В полях панели Сохранить отметим необходимые поля и нажмем Продолжить.

Начнем вычисления нажатием ОК.

Результаты регрессионного анализа приведены в следующих таблицах.

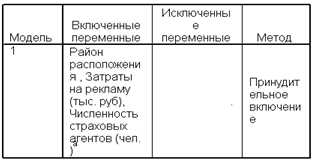
Рис. 1 .5. Перечисление переменных, которые были последовательно исключены на каждом шаге.

При последовательном подборе переменных в SPSS предусмотрена автоматизация, основанная на значимости включения и исключения переменных.

В рис 1. 6. приведены значения коэффициента детерминации, коэффициента множественной корреляции, стандартная ошибка, коэффициент Дарбина-Уотсона последовательно для всех моделей..

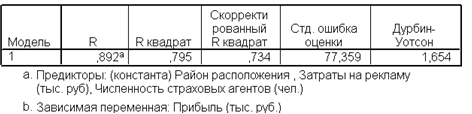
Рис 1.6.  Приведение значений

В рис. 1. 7. приведены результаты дисперсионного анализа и значения F-критерия, полученные на каждом шаге.

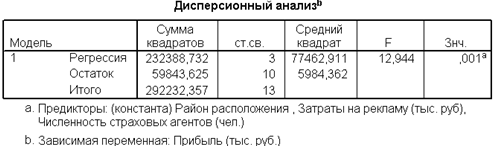
Рис. 1.7. Приведение результатов

В рис. 1.8. в первом столбце указан номер модели, во втором – перечисляются используемые в модели независимые переменные, а в третьем столбце содержатся коэффициенты уравнения регрессии. В четвертом столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, в пятом - стандартизованные коэффициенты, в в шестом – t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.

Уравнение регрессии зависимости прибыли от затраты на рекламу, полученное на последнем шаге, можно записать в следующем виде:

y= 23,023+16,388x₁+6,076x₂

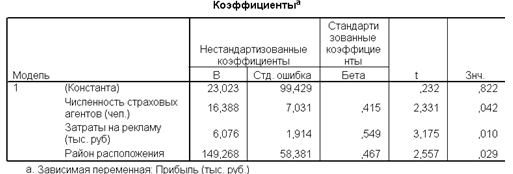
Рис. 1.8. Коэффициенты

Коэффициенты уравнения регрессии показывают, что при увеличении затрат на рекламу на одну тыс. руб. прибыль  увеличиться на 6, 076 млн. руб., при увеличении численности страховых агентов на 1% прибыль увеличится на 16,388 млн. руб. .

4. Оценка качества модели

Уравнение регрессии следует считать признать адекватным, модель считается значимой.(значения R² на рис.1.6,  F-критерия Фишера на рис. 1.7.)

5. Построение прогноза

Для построения прогноза введем прогнозные значения

Затем запустим процедуру Анализ – Регрессия – Линейная.

В полях панели сохранить отметим необходимость сохранения Интервалов предсказания для отдельных значений с вероятностью 90% и нажмем продолжить.

На рис. 1.9. приведены результаты прогнозирования по модели регрессии: точечный прогноз, верхняя и нижняя границы.

С вероятностью 90% прибыль в прогнозируемом месяце составит от 384,97 до 737,73 руб.

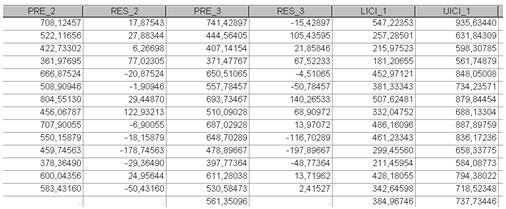
Рис. 1.9. Результаты прогнозирования.

 

ЛАБОРАТОРНАЯ РАБОТА №2

Временные ряды

Задача.

В течение девяти последовательных недель фиксировался спрос Y(t) (млн руб.) на кредитные ресурсы финансовой компании. Временной ряд Y(t) этого показателя приведен ниже в таблице.

Номер наблюдения	1	2	3	4	5	6	7	8	9
данные	3	7	10	11	15	17	21	25	23

Задание.

1. Проверьте наличие аномальных наблюдений.
2. постройте линейную модель Y^(t)=a₀+a₁t, параметры которой оцените МНК (Y(t)) – расчетные, смоделированные значения временного ряда).
3. Оцените адекватность построенных моделей, использую свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использовании R/S- критерия возьмите табулированные границы 2,7-3,7).
4. Оценить адекватность построенных моделей, используя свойства независимости остаточной компоненты, случайности и соответствия нормальному закону распределения (при использование R/S- критерия взять табулированные границы 2,7-3,7).
5. Оценить точность моделей на основе использования средней относительной ошибки аппроксимации.
6. По двум построенным моделям осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р=70%)
7. Фактическое значение показателя, результаты моделирования и прогнозирования представить графически.

Вычисления провести с одним знаком в дробной части. Основные промежуточные результаты вычислений представить в таблицах ( при использовании компьютера представить соответствующие листинги с комментариями.

Решение задачи

Решение задачи начнем с ввода данных непосредственно в SPSS.(рис.2.1)

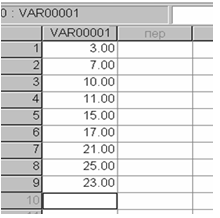
Рис. 2.1 данные задачи представлены в формате SPSS.

Для удобства работы выполним некоторые преобразования файла данных. Используя меню Данные - Задать даты выберем формат Годы, месяцы (рис.2.2)и укажем, что первое наблюдение относится к январю 2005 года. В результате появятся новые переменные Год, Месяц, Дата, изображенные на рис.2.3.

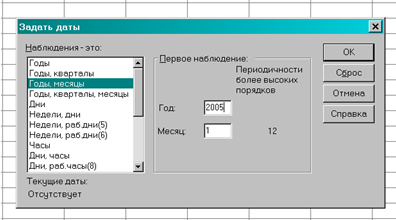
Рис.2.2 используя меню Данные – Задать даты выберем формат Годы, месяцы.

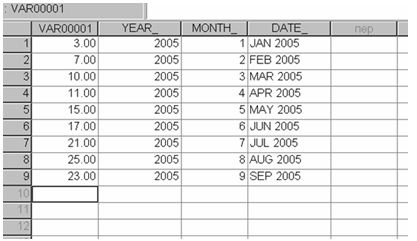
Рис.2.3 Новые переменные: Год, Месяц, Дата.

Параметры модели оценить с помощью МНК.

Для определения параметров модели можно использовать такой способ: Анализ-Регрессия-Подгонка кривых.

• Выберем вид модели Линейная.
• Отметим флажками Включать константу и Графики моделей.
• В полях панели Сохранить отметим необходимые поля и укажем в поле Прогноз до 2006 года месяц 3.

Рис. 2.4. Подгонка кривых. Заполнение поля Сохранить.

Из протокола видно, что мы получили модель:

y^_t=

Построение прогноза.

Прогнозные значения, расположены в последних трех строках редактора данных:

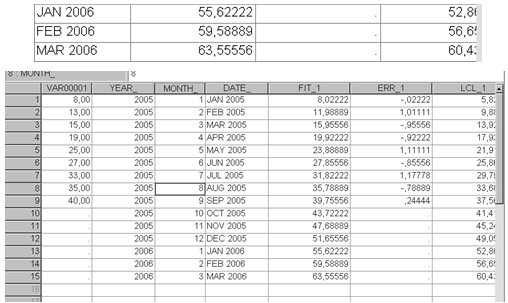
Рис. 2.5. Результаты расчетов: предсказанные значения, значения остаточной компоненты, нижняя и верхняя границы доверительного интервала.

На основании выполненных расчетов можно сделать следующие выводы:

1. Модель имеет вид
2. Размеры платежей составят
3. Денежных средств в объеметыс. руб. на финансирование этого инвестиционного проекта на 3 последующих месяца будут недостаточно(достаточно).

Для построения более наглядного графика выполним редактирование данных. Нажмем в нижней строке  меню кнопку «Переменные».В столбце «Метка» введем расширенное имя переменной. Эта информация будет использована при создании графиков.

Построение графика.

Выберем в верхней строке меню «Графика»-«Линии»-Несколько. В поле Несколько линий: Отдельные значения переменных указываем, что линии представляют переменные : Y(Объем платежей), Предсказанное Y, 90% нижняя граница и 90% верхняя граница.

На рис. 2.6. графики исходного временного ряда Объемы платежей, аппроксимирующая прямая и результаты прогнозирования.

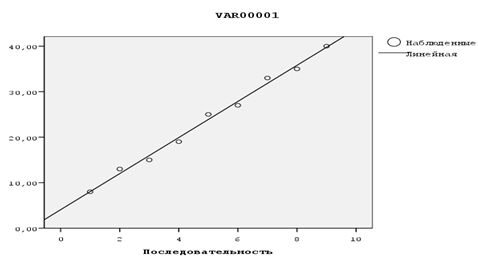
Рис. 2.6. Исходные данные, результаты моделирования и прогнозирования.

Оценка адекватности и точности построенной модели.

Для того чтобы оценить адекватность и точность построенной модели на основе исследования целесообразно  воспользоваться результатами, полученными при расчете линейной регрессии: Анализ-Регрессия-Линейная, где в качестве зависимой переменной указать Y(Объем платежей), в качестве независимой MONTH, и в поле панели Статистики отметить флажками Оценки,критерий Дурбина-Уотсона.

 

ЛАБОРАТОРНАЯ РАБОТА №3

Анализ временных рядов и прогнозирование экономических процессов с использование программы СтатЭксперт

Задание.

1. В «Приложении» выбрать свой расчетныйвариант.
2. Провести анализ временных рядов и прогнозирование экономического показателя в соответствии с излагаемым ниже порядком выполнения работы.
3. Подготовить 4 файла отчета «Стат Эксперт».

Порядок выполнения работы.

1. Создать файл исходныхданныхв среде Ехсеl.

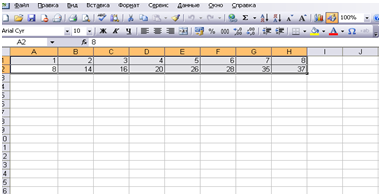
Рис. 3.1  Таблица исходных данных.

2.    Инсталляция  программы  «Стат Эксперт».

«ПУСК»-«ПРОГРАММЫ»-«Olymp»-«Стат Эксперт»-«Включить макросы». Затем дать команду «НАЧАЛО РАБОТЫ»-«ОК».

3.  Включить режимы работы программы

Активировать файл исходных данных, выполнив последовательно действия: «ФАЙЛ»-выбор имени файла в формате Ехсеl. Затем отметить цифровые данные таблицы. После вызвать меню «Стат Экс.», затем «ВРЕМЕННЫЕ РЯДЫ».

1. Предварительная обработка данных.

• Окно «Установка блока данных». Ориентация таблицы: флажок в окно «по строкам», наличие наименований: убрать все флажки в окнах. Затем нажать «Установить».

Рис. 3.2 Окно «Установки блока данных»

• «Окно обработка временных рядов». Этапы обработки: флажок в окно «Предварительный анализ».Затем выделить щелчком левой кнопки мышки «Показатель2» и выполнить команду «Вычислить».

Рис. 3.3 Окно «Обработка временных рядов».

• «Предварительный анализ данных». Оставить все флажки, кроме «Построение графиков». Затем команда «Вычислить».

Получен протокол отчета 1:

Cтатистики временного ряда - Показатель- 2
Базисные характеристики
Наблюдение	Абс. прирост	Темп роста	Темп прироста
2	6.000	175.000	75.000
3	8.000	200.000	100.000
4	12.000	250.000	150.000
5	18.000	325.000	225.000
6	20.000	350.000	250.000
7	27.000	437.500	337.500
8	29.000	462.500	362.500
Цепные характеристики
Наблюдение	Абс. прирост	Темп роста	Темп прироста
2	6.000	175.000	75.000
3	2.000	114.286	14.286
4	4.000	125.000	25.000
5	6.000	130.000	30.000
6	2.000	107.692	7.692
7	7.000	125.000	25.000
8	2.000	105.714	5.714
Средние характеристики
Характеристика	Значение
Среднее арифметическое	23.000
Средний темп роста (%)	124.456
Средний темп прироста (%)	24.456
Средний абсолютный прирост	4.143
Гипотеза об отсутствии тренда
Метод проверки	Результат
Метод Форстера-Стюарта	Нет
Метод сравнения средних	Нет
Вывод: гипотеза отвергается
Проверка однородности данных
Аномальные наблюдения не обнаружены
Автокорреляционная функция
Лаг	Исходный ряд	Разностный ряд (d=1)
1	0.614	-0.699
2	0.274	0.207
Cтандартные отклонения = +0.4878, +0.5077
Частная автокорреляционная функция
Лаг	Исходный ряд	Разностный ряд (d=1)
1	0.715	-1.000
2	-0.165	-0.550
Cтандартные отклонения = +0.3536, +0.4082

1. Построение модели и прогнозирование.
   • Активизировать программу « Olymp»-Стат Эксперт». Затем вызвать исходный файл данных в формате Ехсеl. После вызвать меню «Стат Экс.», затем «ВРЕМЕННЫЕ РЯДЫ».

• Окно « Обработка временных рядов». Флажек в окно «ПОСТРОЕНИЕ МОДЕЛИ И ПРОГНОЗИРОВАНИЕ». Отметить показатель2.

Рис. 3.4. Окно «Обработка временных рядов».

• Окно «Построение модели и прогнозирование». Установить флажки:

• «Модели авторегрессии»;
• «Прогноз вперед»;
• «На основе одной лучшей модели»;
• Период прогноза – 3;
• Вероятность совершения прогноза – 90;

Вычислить.

Составлен протокол отчета 2:

Модели временного ряда -  Показатель- 2
Характеристики базы моделей
Модель	Адекват ность	Точность	Качество
АР(1, 1)	38.306	0.000	9.577
МАФ(1,1)	28.383	49.224	44.014
АР(2, 1)	52.353	0.000	13.088
МАФ(2,1)	26.243	55.057	47.853
Лучшая модель МАФ(2,1)
Параметры моделей
Модель	a1	a2	a3	a4	a5
МАФ(2,1)	-0.029	0.000	0.000	0.000	0.000
Таблица остатков
номер	Факт	Расчет	Ошибка абс.	Ошибка относит.
4	20.000	19.800	0.200	1.000
5	26.000	27.800	-1.800	-6.923
6	28.000	25.800	2.200	7.857
7	35.000	37.800	-2.800	-8.000
8	37.000	34.800	2.200	5.946
Характеристики остатков
Характеристика	Значение
Среднее значение	0.000
Дисперсия	4.160
Приведенная дисперсия	6.933
Средний модуль остатков	1.840
Относительная ошибка	5.945
Критерий Дарбина-Уотсона	3.367
Коэффициент детерминации	0.995
F - значение ( n1 =   1, n2 =   3)	639.404
Критерий адекватности	26.243
Критерий точности	55.057
Критерий качества	47.853
Уравнение значимо с вероятностью 0.95
Таблица прогнозов (p = 90%)
Упреждение	Прогноз	Нижняя граница	Верхняя граница
1	41.200	36.956	45.444
2	45.400	39.677	51.123
3	49.600	43.445	55.755

1. Формирование отчета по графикам.

• Нажать ярлык диаграммы. В появившемся меню выбрать «Аппроксимация и прогноз».

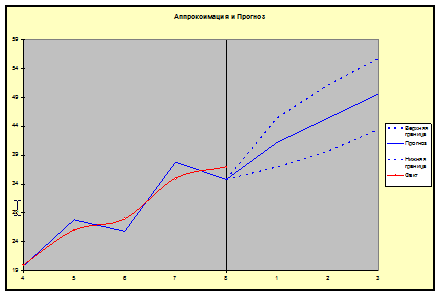
Рис. 3.5. Аппроксимация и прогноз.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Лабораторные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Лабораторные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Лабораторная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---

Похожие работы

• Лабораторная работа №2 по эконометрике (Тема: Временные ряды)
• Временные ряды в эконометрических исследованиях
• Построение модели множественной регрессии