Контрольная по Теории множеств Вариант №2

Тема: Контрольная по Теории множеств Вариант №2

Раздел: Архив

Тип: Контрольная работа | Размер: 117.90K | Скачано: 741 | Добавлен 05.05.17 в 12:32 | Рейтинг: 0 | Еще Контрольные работы

Вариант 2

Теория множеств

№ 1. Найти все подмножества множества {1, 2, 3 }.

Решение:

Выпишем одноэлементные подмножества: {1}, {2}, {3}, затем двухэлементные: {1, 2}, {1, 3}, {2, 3}, трехэлементные: {1, 2, 3} и множество, не содержащее ни одного элемента (пустое множество) – Æ.

Количество подмножеств множества, состоящего из n элементов равно . В нашем примере множество состоит из трех элементов, значит количество подмножеств равно  =8.

 

№ 2. А – множество студентов в одной из групп факультета, а В – множество отличников на факультете. Какие множества студентов описывают множества: АВ; А\В; В\А?

Решение:

Пересечением множеств А и В называется множество АВ, состоящее из всех элементов, которые принадлежат одновременно множеству А и В:

АВ = {х | хА и хВ}.

Тогда АВ – это множество отличников данной группы.

Разностью множеств A и B называется множество А\В элементов, принадлежащих A и не принадлежащих B.

Тогда А\В – множество студентов данной группы, не являющихся отличниками.

В\А – множество отличников факультета за исключением отличников данной группы.

 

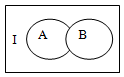
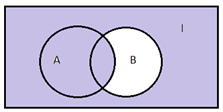
№ 3. Множества А и В есть подмножества множества I (рис.)

Заштриховать на рис. следующие множества:  1) АВ; 2) АВ; 3); 4)

Решение:

1) АВ – объединение множеств А и В (все точки обоих множеств):

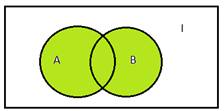
2) АВ – пересечение множеств А и В (общие точки двух множеств):

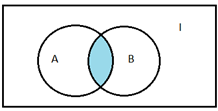
3)  – дополнение множества А (точки, не принадлежащие множеству А):

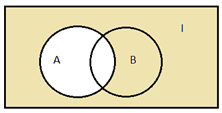
4)  – объединение множества А и дополнения множества В:

 

№ 4. Дано множество К={a;b;{c,d};{e;f;m}}. Определите, какие из следующих высказываний истинны и почему:

а) {a;{c;d}}K;  

б) {c;d}K;    

в){{c;d}}K; 

г){c;d}K. 

Решение: Если любой элемент множества А принадлежит так же и множеству В, то А называют подмножеством В. Записывают А Ì В. Знак Ì называют знаком включения. Знак Î обозначает принадлежность какого-либо элемента к множеству. Поэтому высказывания а), в) и г) являются истинными, а высказывание б) – ложным. Действительно, множество {a;{c;d}}, состоящее из двух элементов a и {c;d} является подмножеством В. Множество {{c;d}}, состоящее из одного элементa {c;d} является подмножеством множества К.  Элемент {c;d} принадлежит множеству К.      А вот множество {c;d}, состоящее из двух элементов с и d не является подмножеством множества К, потому что отдельные элементы с и d не являются элементами множества К.

 

№ 5. Найдите разность множеств P и S, если:

P={x|xZ, -4x6} , S={ x|xN, 3x10}. Здесь Z – множество целых чисел, N - множество натуральных чисел.

Решение:

Разностью множеств P и S называется множество элементов, принадлежащих P и не принадлежащих S. Обозначают P\S и читают "разность P и S". .

Получаем, что разность множеств P и S – это все точки отрезка  за исключением четырех точек  х = 3,4,5,6.

 

№ 6. Найдите дополнение к множеству В до множества А, если

а) А={11;12;43;54;7}, B={7;12}.

Решение:

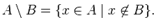
Это множество называют дополнением множества  до множества . (только когда множество В полностью принадлежит множеству А).

Тогда .

б) А – множество учащихся некоторого класса; В – множество отличников в этом классе.

 – множество учащихся данного класса, не являющихся отличниками.

 

№ 7. Даны множества А= {a,b,c},B={1,2} C={2,3,4}.

    Запишите множества  и .

Решение:

Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают А ´ В. Таким образом А ´ В = {(x;y) | x Î A, y Î B}. Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

А ´ В={(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}.

А ´ С={(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4), (c, 2), (c, 3), (c, 4)}.

В ´ С={(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.

 

№ 8. Запишите множество различных цифр в записи числа 235 535. Запишите кортеж цифр этого числа. Какова длина этого кортежа?

Решение:

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами. Так, набор (1, 5, 6) есть кортеж длины 3, так как в нем три элемента.

Множество различных цифр в записи числа 235 535 имеет вид: {2,3,5}.

Кортеж числа 235 535 имеет вид (2; 3; 5; 5; 3; 5). Его длина равна 6.

 

№ 9. Пусть Х={”мама”;“папа”;“рама”;“яма”}; Y={а,м,р,п,я}. Составьте декартово произведение . Отметьте в нем пары, связанные соответствием «В слово х входит буква у».

Решение:

Декартово произведение = { (”мама”, а), (”мама”, м), (”мама”, р), (”мама”, п), (”мама”, я), (“папа”, а), (“папа”, м), (“папа”, р), (“папа”, п), (“папа”, я), (“рама ”, а), (“рама ”, м), (“рама ”, р), (“рама ”, п), (“рама ”, я),    (“яма ”, а), (“яма ”, м), (“яма ”, р), (“яма ”, п), (“яма ”, я)}.

Выделим подчеркиванием среди выписаных пары, связанные соответствием «В слово х входит буква у».

 

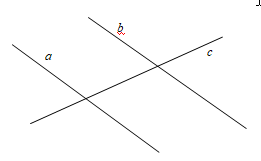
№10. А – множество прямых на плоскости. Выясните, какие из следующих отношений в множесве А являются отношениями эквивалентности.

а) « прямая а перпендикулярна прямой b»

б) “ прямая а паралельна прямой b”

в) “ прямая а пересекает прямую b”.

Решение:

Отношение эквивалентности () на множестве  — это бинарное отношение, для которого выполнены следующие условия:

1. :  для любого  в ,
2. : если , то ,
3. : если  и , то .

а)  «прямая а перпендикулярна прямой b»  не является отношением эквивалентности, т.к. это отношение не рефлексивно: прямая не является перпендикулярной сама себе.

б) “ прямая а паралельна прямой b”  - это отношение эквивалентности:
1) а параллельна а (рефлексивность)
2) а параллельна b ⇒ b параллельна а (симметричность)
3) а параллельна b, b параллельна с ⇒ а параллельна с (транзитивность).

в)  “прямая а пересекает прямую b” – не является отношением эквивалентности, т.к. это отношение не транзитивно: если а параллельна с, а b пересекает обе прямые, то (a,b) и (b,с) находятся в отношении, а (а,с) - нет.

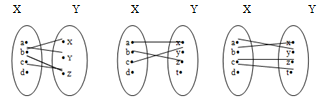
№11.  На рис. изображены графы различных соответствий. Какие из этих соответствий являются отображениями?

Решение:

Отображением (функцией)  f из A в B называется правило, которое каждому элементу множества A сопоставляет некоторый элемент множества B. 

Отношение между элементами множеств Х и Y называется отображением Х в Y, если каждому элементу х из множества Х соответствует только один элемент множества Y. Этот элемент называют образом элемента х при данном отображении:  f(x). На графе такого отображения из каждой точки множества Х будет выходить только одна стрелка.

Следовательно, отображением является только второе соответствие, т.к. у него каждому элементу из Х соответствует только один элемент Y (a®x, b®z, c®y). Соответствия на первом и третьем графах не являются отображениями, так как некоторым элементам Х соответствуют по два-три элемента Y.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---