Главная » Бесплатные рефераты » Бесплатные рефераты по теории вероятностей и математической статистике »
Контрольная работа по Теории вероятностей Вариант №9
Тема: Контрольная работа по Теории вероятностей Вариант №9
Раздел: Бесплатные рефераты по теории вероятностей и математической статистике
Тип: Контрольная работа | Размер: 57.15K | Скачано: 373 | Добавлен 14.04.17 в 19:22 | Рейтинг: 0 | Еще Контрольные работы
1. Пловца в команду принимают следующим образом. Сначала он должен проплыть 100 м за определённое время. Если справится, то 400 м за определённое время. Если и с этим справится, тогда километровую дистанцию за определённое время. Два спортсмена претендуют на место в команде, причём первый вовремя преодолевает соответствующие дистанции с вероятностями 0,7, 0,9 и 0,8, а второй – с вероятностями 0,9, 0,8 и 0,6 соответственно. Какова вероятность того, что в команду:
а) будет принят первый из них;
б) будет принят хотя бы один из них;
в) будут приняты оба;
г) будет принят только один из них?
Решение.
а) Пусть событие A состоит в том, что первый пловец будет принят в команду.
Событие A можно представить в виде произведения трёх независимых событий:
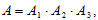
где событие A1 – первый пловец проплывёт 100 м за определённое время;
событие A2 – первый пловец проплывёт 400 м за определённое время;
событие A3 – первый пловец проплывёт 1 км за определённое время.
По условию задачи:
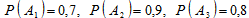
По теореме о вероятности произведения независимых событий найдём вероятность того, что первый пловец будет принят в команду:
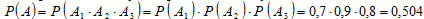
б) Сначала определим вероятность того, что в команду будет принят второй пловец (событие B).
Рассуждая также как для первого пловца, получим:
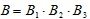
где событие B1 – второй пловец проплывёт 100 м за определённое время;
событие B2 – второй пловец проплывёт 400 м за определённое время;
событие B3 – второй пловец проплывёт 1 км за определённое время;
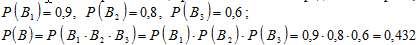
Пусть событие C состоит в том, что в команду не будут приняты ни первый, ни второй пловец.
Событие C можно описать следующим образом:
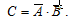
По теореме о вероятности произведения независимых событий:

Поскольку:
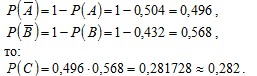
Тогда искомая вероятность события (в команду будет принят хотя бы один пловец) равна:

в) Пусть событие D состоит в том, что в команду будут приняты оба пловца.
Событие D можно описать следующим образом:

По теореме о вероятности произведения независимых событий:

г) Пусть событие E состоит в том, что в команду будет принят только один пловец.
Событие E можно описать следующим образом:
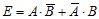
Так как слагаемые в этой сумме несовместны, а сомножители в каждом слагаемом независимы, то:
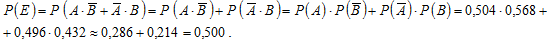
Ответ:
а) вероятность того, что в команду будет принят первый из них, равна 0,504;
б) вероятность того, что в команду будет принят хотя бы один из них, равна 0,718;
в) вероятность того, что в команду будут приняты оба, равна 0,218;
г) вероятность того, что в команду будет принят только один из них, равна 0,500.
2. В команде три стрелка, которые попадают в цель с вероятностью 0,9, пять стрелков, попадающих с вероятностью 0,8, и тринадцать, попадающих с вероятностью 0,7. Для зачётного выстрела стрелок определяется жребием. Какова вероятность того, что он попадёт в цель?
Решение.
Пусть событие A – выбранный стрелок попадёт в цель.
Выдвинем гипотезы:
H1 – выбран стрелок из 1-й группы;
H2 – выбран стрелок из 2-й группы;
H3 – выбран стрелок из 3-й группы.
Вероятности гипотез найдём по классическому определению вероятности:
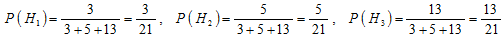
Условные вероятности события A известны:
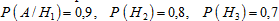
Вероятность события A найдём по формуле полной вероятности:
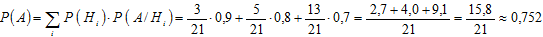
Ответ: вероятность того, что наудачу выбранный стрелок попадёт в цель, равна 0,752.
3. Известно, что на собеседовании при приёме на работу в среднем каждый пятый претендент завышает свою предыдущую зарплату.
Составить закон распределения случайной величины – числа претендентов на собеседовании, честно сообщивших о своей предыдущей зарплате, среди 4 претендентов.
Найти её математическое ожидание, дисперсию, среднее квадратическое отклоне-ние, построить функцию распределения.
Решение.
По статистическому определению вероятности, вероятность того, что при приёме на работу претендент завысит свою предыдущую зарплату, равна

значит, не завысит свою предыдущую зарплату с вероятностью 1-0,2=0,8 .
Случайная величина x – число претендентов из 4-х, честно сообщивших о своей предыдущей зарплате на собеседовании – может принимать значения 0, 1, 2, 3 или 4. При этом вероятности этих значений будут определяться по формуле Бернулли:
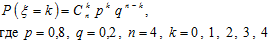
Вычислим вероятность каждого значения случайной величины x:
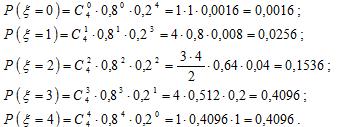
Составим закон распределения случайной величины x:
|
|
|
|
|
|
|
|
|
хi |
0 |
1 |
2 |
3 |
4 |
∑рi |
|
рi |
0,0016 |
0,0256 |
0,1536 |
0,4096 |
0,4096 |
1,0000 |
|
|
|
|
|
|
|
|
Поскольку вероятности значений случайной величины x находились по формуле Бернулли, то эта случайная величина имеет биномиальное распределение. Следовательно, её числовые характеристики будут определяться значениями n, p, q:
математическое ожидание:
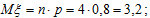
дисперсия:
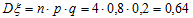
Найдём функцию распределения, используя формулу

Построим график функции распределения случайной величины x.
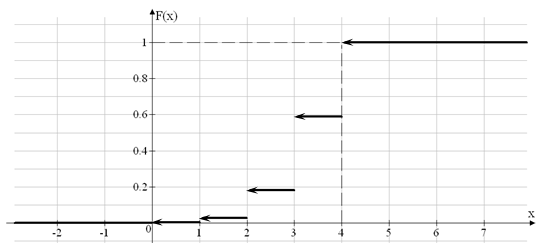
Ответ: 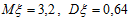
4. Случайные величины x и h независимы и имеют геометрические распределения с параметрами p = 0,5 для величины x и p = 0,4 для величины h. Найти математическое ожидание и дисперсию величины g = 2x – 3h.
Решение.
Математическое ожидание и дисперсия случайной величины x, имеющей геометрическое распределение с параметром p=0.5, равны:

Аналогично находим математическое ожидание и дисперсию случайной величины h, имеющей геометрическое распределение с параметром p=0.4:

Случайные величины x и h независимы. Используем свойства математического ожидания и дисперсии для нахождения числовых характеристик случайной величины 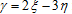 :
:

Ответ: 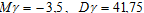
5. Дан закон распределения двумерной случайной величины (x, h):
|
|
|
|
|
|
|
|
x = -2 |
x = 0 |
x = 1 |
x = 2 |
|
h = 1 |
0,04 |
0,1 |
0,02 |
0,04 |
|
h = 2 |
0,04 |
0,1 |
0,02 |
0,04 |
|
h = 4 |
0,12 |
0,3 |
0,06 |
0,12 |
|
|
|
|
|
|
1) Выписать одномерные законы распределения случайных величин x и h, вычислить математические ожидания Mx, Mh и дисперсии Dx, Dh.
2) Найти ковариацию Cov(x, h) и коэффициент корреляции r(x, h).
3) Являются ли случайные величины x и h зависимыми?
4) Составить условный закон распределения случайной величины g = (x|h = 2) и найти Mg и Dg.
Решение.
1) Найдём одномерный закон распределения случайной величины x, суммируя в законе распределения двумерной случайной величины (x, h) вероятности по столбцам:
|
|
|
|
|
|
|
x |
-2 |
0 |
1 |
2 |
|
p(x) |
0,2 |
0,5 |
0,1 |
0,2 |
|
|
|
|
|
|
Вычислим математическое ожидание, дисперсию и среднее квадратическое откло-нение случайной величины x:

Найдём одномерный закон распределения случайной величины h, суммируя в законе распределения двумерной случайной величины (x, h) вероятности по строкам:
|
h |
1 |
2 |
4 |
|
p(h) |
0,2 |
0,2 |
0,6 |
Вычислим математическое ожидание, дисперсию и среднее квадратическое откло-нение случайной величины h:

2) Вычислим ковариацию (корреляционный момент) случайных величин x и h:
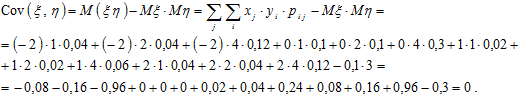
Вычислим коэффициент корреляции случайных величин x и h:
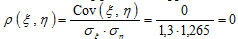
3) Поскольку , то случайные величины x и h независимые.
4) Найдём вероятности случайной величины по формуле:

Имеем:

Таким образом, искомый условный закон распределения имеет вид:
|
g |
-2 |
0 |
1 |
2 |
|
p(g) |
0,2 |
0,5 |
0,1 |
0,2 |
Заметим, что законы распределения случайных величин g и x одинаковы, поэтому:

Ответ:
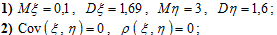
3) случайные величины x и h независимые;

Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).
Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.
Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.
Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.
Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.
Добавление отзыва к работе
Добавить отзыв могут только зарегистрированные пользователи.
![Контрольная работа по Теории вероятностей Вариант №9 [14.04.17]](/files/works_screen/3/39/57.png)