Контрольная по Эконометрике Вариант №6

Тема: Контрольная по Эконометрике Вариант №6

Раздел: Бесплатные рефераты по эконометрике

Тип: Контрольная работа | Размер: 399.91K | Скачано: 355 | Добавлен 06.04.17 в 07:21 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Российский экономический университет имени Г.В. Плеханова

Год и город: Пермь 2017

Содержание

Задача 1. 3

Задача 2. 9

Задача 3. 15

Задача 4. 17

Задача 5. 19

Список литературы.. 22

 

Задача 1

Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей Х (тыс. км) и стоимостью технического обслуживания У (тыс. руб.). Для выяснения этой связи было отобрано 10 автомобилей:

Х	6	7	8	9	10	12	9	8	12	15
У	13	16	15	20	19	14	10	9	11	18

1. Постройте поле корреляции результата и фактора и сформулируйте гипотезу о форме связи.
2. Определите параметры уравнений парной линейной регрессии и дайте интерпретацию коэффициента регрессии b. Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
3. С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии b и уравнения регрессии в целом. Сделайте выводы.
4. С вероятностью 0,95 постройте доверительный интервал ожидаемого значения результативного признака, если факторный признак увеличится на 5% от своего среднего значения.

Решение

1. На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.

Линейное уравнение регрессии имеет вид y = bx + a

Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.

Для оценки параметров α и β - используют МНК (метод наименьших квадратов).

Система нормальных уравнений.

a•n + b∑x = ∑y

a∑x + b∑x² = ∑y•x

Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

x	y	x2	y2	x • y
6	13	36	169	78
7	16	49	256	112
8	15	64	225	120
9	20	81	400	180
10	19	100	361	190
12	14	144	196	168
9	10	81	100	90
8	9	64	81	72
12	11	144	121	132
15	18	225	324	270
96	145	988	2233	1412

Для наших данных система уравнений имеет вид

10a + 96 b = 145

96 a + 988 b = 1412

Получаем эмпирические коэффициенты регрессии: b = 0.3012, a = 11.6084

Уравнение регрессии (эмпирическое уравнение регрессии):

y = 0.3012 x + 11.6084

2. Параметры уравнения регрессии.

Выборочные средние.

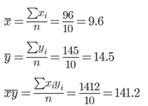
Выборочные дисперсии:

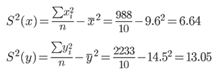
Среднеквадратическое отклонение

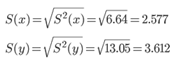
Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:

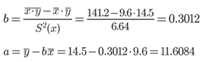
Коэффициент корреляции

Ковариация.

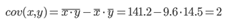
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

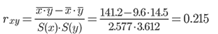
Линейный коэффициент корреляции принимает значения от –1 до +1.

В нашем примере связь между признаком Y фактором X слабая и прямая.

Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:

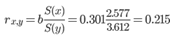
Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = 0.301 x + 11.608

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = 0.301 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.301.

Коэффициент a = 11.608 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.

Коэффициент эластичности находится по формуле:

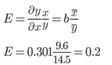
Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.

Бета – коэффициент

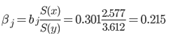
Т.е. увеличение x на величину среднеквадратического отклонения S_x приведет к увеличению среднего значения Y на 21.5% среднеквадратичного отклонения S_y.

Ошибка аппроксимации.

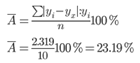
В среднем, расчетные значения отклоняются от фактических на 23.19%. Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии.

Эмпирическое корреляционное отношение.

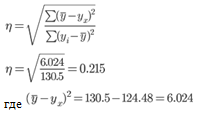
3. Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X_p = 0.95

t_крит (n-m-1;α/2) = (8;0.025) = 2.306

y(0.95) = 0.301*0.95 + 11.608 = 11.895

Вычислим ошибку прогноза для уравнения y = bx + a

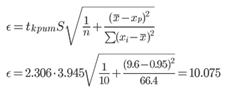
11.895 ± 10.075

(1.82;21.97)

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

Вычислим ошибку прогноза для уравнения y = bx + a + ε

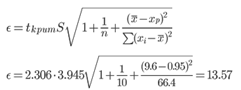
11.895 ± 13.57

(-1.68;25.47)

4. Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (b - t_крит S_b; b + t_крит S_b)

(0.3 - 2.306 • 0.48; 0.3 + 2.306 • 0.48) 

 (-0.815;1.417)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента b статистически незначима.

(a - t_крит S_a; a + t_крит S_a)

(11.608 - 2.306 • 4.81; 11.608 + 2.306 • 4.81)

(0.513;22.704)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

2) F-статистика. Критерий Фишера.

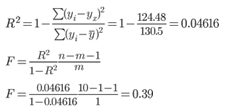
Табличное значение критерия со степенями свободы k₁=1 и k₂=8, F_табл = 5.32

Отметим значения на числовой оси.

Принятие H0	Отклонение H0, принятие H1
95%	5%
0.39	5.32

Поскольку фактическое значение F < F_табл, то коэффициент детерминации статистически не значим (Найденная оценка уравнения регрессии статистически не надежна).

 

Задача 2

Для анализа эффективности работы предприятий машиностроения были получены следующие данные:

№	Рентабельность (прибыль в $)	Производит. труда, млн. руб. на 1 раб.	Средний возраст производственного оборудования
1	7	7	20
2	8	10	19
3	7	9	21
4	9	11	17
5	9	11	16
6	8	11	18
7	11	17	15
8	11	14	14
9	16	13	10
10	15	18	10

1. Постройте линейное уравнение множественной регрессии и поясните экономический смысл его параметров
2. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции, сделайте выводы.
3. Дайте оценку полученного уравнения на основе коэффициента детерминации и общего F-критерия Фишера.

Решение

1. Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (X^TX)^-1X^TY
К матрице с переменными X_j добавляем единичный столбец:

1	7	20
1	10	19
1	9	21
1	11	17
1	11	16
1	11	18
1	17	15
1	14	14
1	13	10
1	18	10

Матрица Y

7
8
7
9
9
8
11
11
16
15

Матрица X^T

1	1	1	1	1	1	1	1	1	1
7	10	9	11	11	11	17	14	13	18
20	19	21	17	16	18	15	14	10	10

Умножаем матрицы, (X^TX)

XT X =

10 121 160 121 1571 1841 160 1841 2692

В матрице, (X^TX) число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы X^T и 1-го столбца матрицы X

Умножаем матрицы, (X^TY)

XT Y =

101 1297 1509

Находим обратную матрицу (X^TX)^-1

(XT X) -1 = =

16,514 -0,613 -0,562 -0,613 0,026 0,0187 -0,562 0,0187 0,021

Вектор оценок коэффициентов регрессии равен

Y(X) =

16,514 -0,613 -0,562 -0,613 0,026 0,0187 -0,562 0,0187 0,021

*

101 1297 1509

=

24,361 -0,0547 -0,85

Уравнение регрессии (оценка уравнения регрессии)

Y = 24.3615-0.05471X₁-0.85X₂

2. Матрица парных коэффициентов корреляции R.

Число наблюдений n = 10. Число независимых переменных в модели равно 2, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 4. Матрица, независимых переменных Х имеет размерность (10 х 4).

Матрица A, составленная из Y и X

1	7	7	20
1	8	10	19
1	7	9	21
1	9	11	17
1	9	11	16
1	8	11	18
1	11	17	15
1	11	14	14
1	16	13	10
1	15	18	10

Транспонированная матрица.

1	1	1	1	1	1	1	1	1	1
7	8	7	9	9	8	11	11	16	15
7	10	9	11	11	11	17	14	13	18
20	19	21	17	16	18	15	14	10	10

Матрица A^TA.

10	101	121	160
101	1111	1297	1509
121	1297	1571	1841
160	1509	1841	2692

Полученная матрица имеет следующее соответствие:

∑n	∑y	∑x1	∑x2
∑y	∑y2	∑x1 y	∑x2 y
∑x1	∑yx1	∑x1 2	∑x2 x1
∑x2	∑yx2	∑x1 x2	∑x2 2

Найдем парные коэффициенты корреляции.

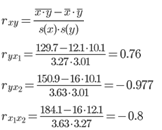
Признаки x и y	∑xi		∑yi		∑xiyi
Для y и x1	121	12.1	101	10.1	1297	129.7
Для y и x2	160	16	101	10.1	1509	150.9
Для x1 и x2	160	16	121	12.1	1841	184.1

Дисперсии и среднеквадратические отклонения.

Признаки x и y
Для y и x1	10.69	9.09	3.27	3.015
Для y и x2	13.2	9.09	3.633	3.015
Для x1 и x2	13.2	10.69	3.633	3.27

Матрица парных коэффициентов корреляции R:

-	y	x1	x2
y	1	0.7598	-0.9768
x1	0.7598	1	-0.7997
x2	-0.9768	-0.7997	1

Рассчитаем наблюдаемые значения t-статистики для r_yx1 по формуле:

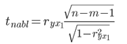
где m = 1 - количество факторов в уравнении регрессии.

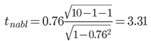
По таблице Стьюдента находим Tтабл

t_крит(n-m-1;α/2) = (8;0.025) = 2.306

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим

Рассчитаем наблюдаемые значения t-статистики для r_yx2 по формуле:

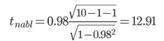
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим

Частные коэффициенты корреляции.

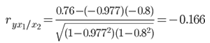
Теснота связи низкая.

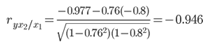
Теснота связи сильная

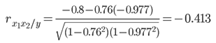
Теснота связи не сильная

Множественный коэффициент корреляции (Индекс множественной корреляции).

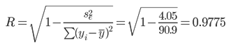
Коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

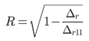
где Δ_r - определитель матрицы парных коэффициентов корреляции; Δ_r11 - определитель матрицы межфакторной корреляции.

∆ r =

1 0,76 -0,977 0,76 1 -0,8 -0,977 -0,8 1

= 0.0161

 

∆ r11 =

1 -0,8 -0,8 1

= 0.36

Коэффициент множественной корреляции

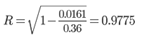
Аналогичный результат получим при использовании других формул:

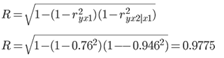
Связь между признаком Y и факторами X_i сильная

3. Коэффициент детерминации.

R²= 0.9775² = 0.9554

Более объективной оценкой является скорректированный коэффициент детерминации:

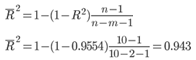
Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y.

Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.

F-статистика. Критерий Фишера.

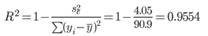
Проверим гипотезу об общей значимости - гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

H₀: R² = 0; β₁ = β₂ = ... = β_m = 0.

H₁: R² ≠ 0.

Проверка этой гипотезы осуществляется с помощью F-статистики распределения Фишера (правосторонняя проверка).

Если F < F_kp = F_{α ; n-m-1}, то нет оснований для отклонения гипотезы H₀.

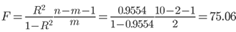
Табличное значение при степенях свободы k₁ = 2 и k₂ = n-m-1 = 10 - 2 - 1 = 7, Fkp(2;7) = 4.74

Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно.

 

Задача 3

Ниже приводится макроэкономическая модель спроса и предложения кейнсианского типа:

Q_t^S=a₀ +a₁P_t + a₂P_t-1 +u₁ (предложение)

Q_t^d= b₀+b₁P_t + b₂P_t + b₃Y_t +u₂ (спрос)

Q_t^S=Q_t^d (тождество)

где Q_t^d –спрос на товар в период t; Q_t^S предложение товара в момент t; Р_t –цена товара в моменты t и t-1; У_t –доход в момент t; u1, u₂– случайные ошибки.

1. проверьте с помощью порядкового условия идентификации, идентифицирована ли данная модель.
2. Выпишите приведенную форму модели.
3. Укажите, каким методом вы будете определять структурные параметры каждого уравнения, кратко опишите методику расчета.

Решение

Разумно предположить, что среднеквадратическое отклонение ошибки прямо пропорционально I.

1) Нормирование. Пронормировать рассматриваемую модель можно, разделив ее на I :

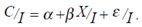
Можно использовать для нормировки (взвешивания) и переменную, не входящую в модель. Обозначим ее N:

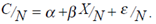
Нормирование равнозначно использованию взвешенного метода наименьших квадратов. Как веса для номинальных величин можно использовать уровень цен, получив тем самым реальные величины. Как веса для стран можно использовать население, получив тем самым среднедушевые показатели (потребление на душу населения и т. п.).

2) Логарифмирование. Прологарифмировав уравнение C = α I + ξ при

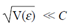
можно получить следующее линейное приближение:

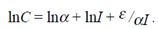
Вряд ли можно привести теоретические возражения и против того, чтобы сразу использовать линейную в логарифмах модель (эта форма модели сокращенно называется логлинейной), например,

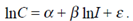
"Кандидатами" на логарифмирование в первую очередь служат те переменные, которые заведомо могут принимать только положительные  значения. Один из их признаков, это то, что, как правило, интересуются относительными приростами таких переменных, а не абсолютными приростами. В экономике это следующие величины: физические объемы благ, цены, стоимостные показатели, различные индексы.

 

Задача 4

Имеются данные об уровне безработицы в регионе:

Месяц	Уровень безработицы, %
январь	8,9
февраль	8,6
март	8,4
апрель	8,1
май	7,9
июнь	7,6
июль	7,3
август	7,2
сентябрь	7,0

1. Определите коэффициент автокорреляции первого порядка и дайте его интерпретацию.
2. Обоснуйте выбор вида уравнения тренда и определите его параметры.
3. Дайте прогноз уровня безработицы на ближайший следующий год. Постройте доверительный интервал прогноза.

Решение

1. Расчет коэффициента автокорреляции 1-го порядка.

Параметры уравнения авторегрессии.

Выборочные средние.

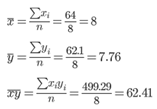
Выборочные дисперсии:

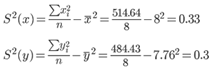
Среднеквадратическое отклонение.

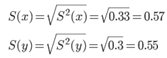
Коэффициент автокорреляции.

Линейный коэффициент автокорреляции r_t,t-1:

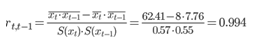
Линейный коэффициент корреляции принимает значения от –1 до +1.

В нашем примере связь между рядами - весьма высокая и прямая.

x	y	x2	y2	x • y
8.9	8.6	79.21	73.96	76.54
8.6	8.4	73.96	70.56	72.24
8.4	8.1	70.56	65.61	68.04
8.1	7.9	65.61	62.41	63.99
7.9	7.6	62.41	57.76	60.04
7.6	7.3	57.76	53.29	55.48
7.3	7.2	53.29	51.84	52.56
7.2	7.0	51.84	49.00	50.40
64	62.1	514.64	484.43	499.29

1. Значимость коэффициента автокорреляции.

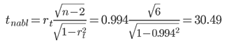
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=6 находим t_крит:

t_крит (n-m-1;α/2) = (6;0.025) = 2.447

где m = 1 - количество объясняющих переменных.

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента автокорреляции. Другими словами, коэффициент автокорреляции статистически - значим

3. Интервальная оценка для коэффициента автокорреляции (доверительный интервал).

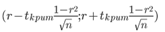
Доверительный интервал для коэффициента корреляции

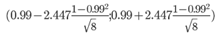
r(0.98;1)

Частный коэффициент корреляции:

Ф₁ = r₁

Лаг (порядок)	rt,t-L	Коррелограмма
1	0.9936	*****

Вывод: в данном ряду динамики имеется тенденция (r_t,t-1 = 0.994 → 1). 

 

Задача 5

Исследуется зависимость объема продаж бензина от динамики потребительских цен.  Были получены следующие данные:

Квартал	1	2	3	4	5	6	7	8	9
Индекс потребительских цен (в процентах к 9 кварталу)	139	132	126	121	117	112	106	100	100
Средний за день объем продаж бензина в течение квартала (тыс. литров)	65	68	72	75	77	80	83	85	89

1. Определите коэффициент корреляции между временными рядами объема продаж бензина и уровня инфляции:
   • по исходным уровням ряда,
   • по первым разностям уровней рядов.
2. Сделайте выводы о тесноте связи между временными рядами объема продаж бензина и уровня инфляции.

Решение

1. Для оценки параметров α и β - используют МНК (метод наименьших квадратов).

Система нормальных уравнений.

a•n + b∑x = ∑y

a∑x + b∑x² = ∑y•x

Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

x	ln(y)	x2	ln(y)2	x • ln(y)
139	4.174	19321	17.426	580.24
132	4.22	17424	17.804	556.975
126	4.277	15876	18.29	538.86
121	4.317	14641	18.641	522.416
117	4.344	13689	18.869	508.225
112	4.382	12544	19.202	490.787
106	4.419	11236	19.526	468.397
100	4.443	10000	19.737	444.265
100	4.489	10000	20.148	448.864
1053	39.064	124731	169.642	4559.029

Для наших данных система уравнений имеет вид

9a + 1053 b = 39.06

1053 a + 124731 b = 4559.03

Получаем эмпирические коэффициенты регрессии: b = -0.00749, a = 5.2168
Уравнение регрессии (эмпирическое уравнение регрессии):

y = e^5.21681176e^-0.00749x = 184.34551e^-0.00749x

Выборочные средние.

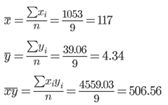
Выборочные дисперсии:

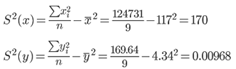
Среднеквадратическое отклонение

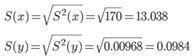
Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:

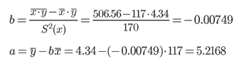
2. Коэффициент эластичности находится по формуле:

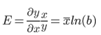
E = 117(-0.00749) = -0.88

Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.

Эмпирическое корреляционное отношение.

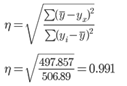
где

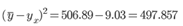
Индекс корреляции.

Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.

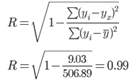
Полученная величина свидетельствует о том, что фактор x существенно влияет на y

 

Список литературы

1. Алексеев А.Р. Экономическая статистика : учебник для вузов / [Алексеев А.Р., Воробьев А.Н., Громыко Г.Л., и др.] ; под ред. Ю.Н. Иванова. - М.: ИНФРА-М, 2007. - 734 с.
2. Бабешко Л.О. Основы эконометрического моделирования : учеб. пособие / Л. О. Бабешко. - Изд. 4-е. - М. : КомКнига, 2010. - 428 с.
3. Гладилин, А. В. Эконометрика: учебное пособие для вузов/А. В. Гладилин, А. Н. Герасимов, Е. И. Громов.-2-е изд., стереотип.-М.:КНОРУС,2008.-226
4. Ильченко А.Н. Практикум по экономико-математическим методам: учеб. пособие / А. Н. Ильченко, О. Л. Ксенофонтова, Г. В. Канакина. - М.: Финансы и статистика: ИНФРА-М, 2009. - 287 с.
5. Кочетыгов А.А. Основы эконометрики : учеб. пособие для вузов / А. А. Кочетыгов, Л. А. Толоконников. - М. ; Ростов н/Д : МарТ, 2007. - 343 с.
6. Красс М.С. Математика в экономике. Математические методы и модели : учеб. для вузов / М. С. Красс, Б. П. Чупрынов. - М. : Финансы и статистика, 2007. - 541 с.
7. Орлов А.И. Эконометрика : учебник / А.И. Орлов. – М. : Изд-во «Экзамен», 2002. - 576 с.
8. Салин В.Н. Социально-экономическая статистика : учебник / В.Н. Салин, Е.П. Шпаковская. - М. : Юристъ, 2001. - 457 c.
9. Тихомиров Н. П. Эконометрика : учебник для вузов / Н. П. Тихомиров, Е. Ю. Дорохина. - М. : Экзамен, 2003. - 512 с.
10. Эконометрика : учебник для вузов / под ред. Ю.Н. Иванова. - М. : ИНФРА-М, 2008. - 735 с.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---