Контрольная работа №2 по Теории вероятностей

Тема: Контрольная работа №2 по Теории вероятностей

Раздел: Бесплатные рефераты по теории вероятностей и математической статистике

Тип: Контрольная работа | Размер: 102.57K | Скачано: 317 | Добавлен 24.03.17 в 10:45 | Рейтинг: 0 | Еще Контрольные работы

Контрольная работа № 2

Задача 1. Из 1560 сотрудников предприятия по схеме собственно случайной бесповторной выборки отобрано 100 человек для получения статистических данных о пребывании на больничном листе в течение года. Полученные данные представлены в таблице::

Таблица 1

Количество дней пребывания на больничном листе	Менее 3	3-5	5-7	7-9	9-11	Более 11	Итого
Число сотрудников	6	13	24	39	8	10	100

Найти:

а) вероятность того, что среднее число дней пребывания на больничном листе среди сотрудников предприятия отличается от их среднего числа в выборке не более чем на 1 день (по абсолютной величине);

б) границы, в которых с вероятностью 0,95 заключена доля всех сотрудников, пребывающих на больничном листе не более 7 дней;

в) объем бесповторной выборки, при котором те же границы для доли, (см. п. б)), можно гарантировать с вероятностью 0,98.

Решение:

Все необходимые расчеты проведены в режиме MS Excel и сведены в таблицу 1.

а) вероятность того, что среднее число дней пребывания на больничном листе среди сотрудников предприятия отличается от их среднего числа в выборке не более чем на 1 день (по абсолютной величине) найдем из формулы:

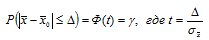
Выполним промежуточные вычисления:

∆=1 по условию (предельная ошибка выборки);

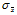  - средняя квадратическая ошибка, которая для бесповторной выборки  рассчитывается по формуле:

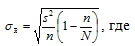
 - выборочная дисперсия, равная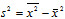

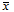 - выборочная средняя

n – объем выборки (n=100)

N – объем всей совокупности (N=1560).

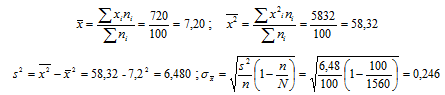
Тогда

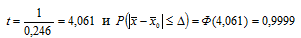
Таблица 1

Количество дней пребы-вания на больничном листе	Середина ряда, x(i)	Число сотрудников n(i)	x(i)n(i)	x2(i)n(i)
менее 3	2	6	12	24
3-5	4	13	52	208
5-7	6	24	144	864
7-9	8	39	312	2496
9-11	10	8	80	800
более 11	12	10	120	1440
ИТОГО	42	100	720	5832

б) границы, в которых с вероятностью 0,95 заключена доля всех сотрудников, пребывающих на больничном листе не более 7 дней

Имеем n=100, N=1560, m=6+13+24 = 43.

Выборочная доля всех сотрудников, пребывающих на больничном листе не более 7 дней находится по формуле:

Средняя квадратическая ошибка выборки для доли при бесповторной выборке равна:

Тогда искомые границы найдем из формул:

где Δ=tσ_w – ошибка выборки. Значение t найдем из табличных данных для функции Лапласса:

Ф(t)=0,95à t=1,96тогда Δ=1,96×0,048=0,094, следовательно:

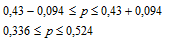
Таким образом, границы, в которых с вероятностью 0,95 заключена доля всех сотрудников, пребывающих на больничном листе не более 7 дней есть интервал от 0,336 до 0,524.

в) объем бесповторной выборки, при котором те же границы для доли, (см. п. б)), можно гарантировать с вероятностью 0,98

γ=0,98 à t=2,33

Объем бесповторной выборки найдем по формуле:

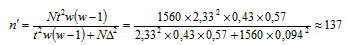
Таким образом, для того чтобы с вероятностью 0,98 можно было утверждать, что доля всех сотрудников, пребывающих на больничном листе не более 7 дней есть интервал от 0,336 до 0,524, необходимо опросить 137 сотрудников.

 

Задача 2. По данным задачи 1, используя χ² – критерий Пирсона, при уровне значимости α=0,05 проверить гипотезу о том, что случайная величина ξ – число дней пребывания сотрудников предприятия на больничном листе – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

Решение:

Проверим гипотезу: случайная величина ξ –д число дней пребывания сотрудников предприятия на больничном листе – распределена по нормальному закону с параметрами: а=7,2, σ² = 6,48 т.е.  ξ ~N(7,2; 6,48).

Для расчета вероятностей pi попадания случайной величины ξ в интервал [xi, xi+1] используем функцию Лапласа:

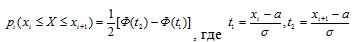
Выполним промежуточные вычисления:

Используя табличные значения для функции Лапласа, получим:

Ф(-2,83)=-Ф(2,83)=-0,9953   Ф(-1,65)=-Ф(1,65)= -0,9011 

Ф(-0,86)=-Ф(0,86)=-0,6629   Ф(-0,08)=-Ф(0,08)=-0,0638   Ф(0,71)=0,5223 Ф(1,49)=0,8638   Ф(140,56)=0,9999

Вероятности pi попадания случайной величины Х в интервал [xi, xi+1] равны:

По полученным значениям вероятностей строим нормальную кривую на одном чертеже с гистограммой:

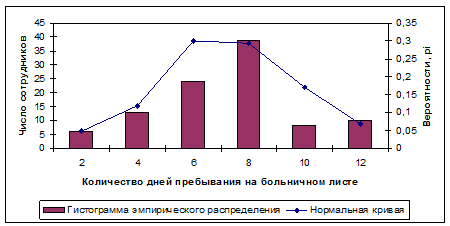
Затем по формуле:

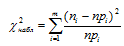
рассчитаем значение статистики.

Полученные значения сведем в таблицу 3:

Таблица 3

Количество дней пребывания на больничном листе				Середина ряда, xi	Число сотрудников ni	xini	x2ini	Частость, wi	t1	t2	Ф(t1)	Ф(t2)	Вероятности, pi	Теоретич. частоты, npi	(ni-npi)2	(ni-npi)2/npi
менее			3	2	6	12	24	0,060	-2,83	-1,65	-0,9953	-0,9011	0,0471	4,71	1,664	0,353
3	-		5	4	13	52	208	0,130	-1,65	-0,86	-0,9011	-0,6629	0,1191	11,91	1,188	0,100
5	-		7	6	24	144	864	0,240	-0,86	-0,08	-0,6629	-0,0638	0,29955	29,955	35,462	1,184
7	-		9	8	39	312	2496	0,390	-0,08	0,71	-0,0638	0,5223	0,29305	29,305	93,993	3,207
9	-		11	10	8	80	800	0,080	0,71	1,49	0,5223	0,8638	0,17075	17,075	82,356	4,823
более			11	12	10	120	1440	0,100	1,49	140,56	0,8638	0,9999	0,06805	6,805	10,208	1,500
ИТОГО				42	100	720	5832	1,000					1,00	99,76	224,87	11,17

Итак, фактически наблюдаемое значение статистики χ²_набл = 11,17. Соответствующее критическое значение статистики χ² по таблице χ²_0,05;6-2-1 = 7,82. Т.к. χ²_набл > χ²_0,05;3, то гипотеза о выбранном теоретическом нормальном законе N(7,2; 6,48) не подтверждается.

 

Задача 3. Распределение 110 образцов полимерных композиционных материалов по содержанию в них нефтешламов ξ (%) и водопоглощению ƞ (%) представлено в таблице:

Таблица 1

ƞ ξ	15-25	25-35	35-45	45-55	55-65	65-75
5-15	17	4
15-25	3	18	3
25-36		2	15	5
35-45			3	13	7
45-55					6	14
Итого	20	24	21	18	13	14

Необходимо:

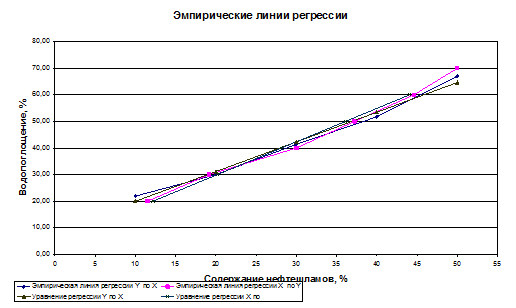
1) Вычислить групповые средние  и , построить эмпирические линии регрессии.

2) Предполагая, что между переменными ξ и ƞ существует линейная корреляционная зависимость:

а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;

б) вычислить коэффициент корреляции, на уровне α=0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными ξ и ƞ;

в) используя соответствующее уравнение регрессии, оценить средний процент водопоглощения в образцах, содержащих 35 % нефтешламов.

Решение:

1) Вычислим групповые средние  и  по формулам:

Полученные данные занесем в корреляционную таблицу 2:

Таблица 2

Содержание нефтешламов, %, ξ	Середины интервалов	Водопоглощение,% ƞ						Итого ni	Групповая средняя,
	yi     xi	15-25	25-35	35-45	45-55	55-65	65-75
		20	30	40	50	60	70
5-15	10	17	4					21	21,90
15-25	20	3	18	3				24	30,00
25-36	30		2	15	5			22	41,36
35-45	40			3	13	7		23	51,74
45-55	50					6	14	20	67,00
Итого nj		20	24	21	18	13	14	110	212,008
Групповая средняя,		11,50	19,17	30,00	37,22	44,62	50,00

Построим эмпирические линии регрессии:

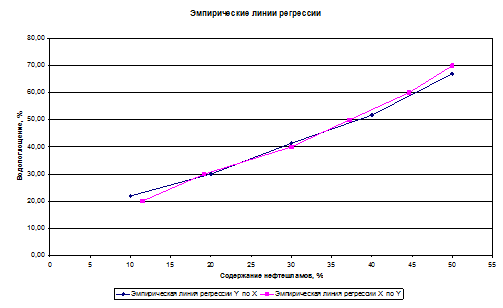
2) Предполагая, что между переменными ξ и ƞ существует линейная корреляционная зависимость:

а) найдем выборочные уравнения регрессии. Уравнения регрессии имеют вид:

- выборочные коэффициенты регрессии;

- выборочный корреляционный момент или выборочная ковариация;

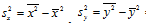- выборочные дисперсия переменных.

Для вычисления всех коэффициентов найдем необходимые суммы.

Все промежуточные расчеты выполнены в MS Excel и сведены в таблицу 3.

Затем находим выборочные характеристики и параметры уравнений регрессии:

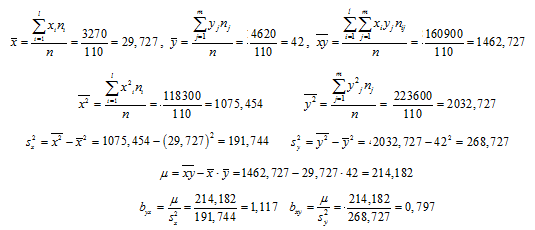
Итак, уравнения регрессии:

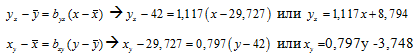
Экономическая интерпретация полученных уравнений:

• из уравнения регрессии Y по Х следует, что при увеличении Х (ξ) – содержание нефтешламов в полимерных композиционных материалах на 1% мы получим увеличение водопоглощения Y (ƞ) на 1,117%;
• из уравнения регрессии Х по Y следует, что для того, чтобы получить увеличение водопоглощения Y (ƞ) на 1 % необходимо увеличить содержание нефтешламов в полимерных композиционных материалах Х(ξ) на 0,797 %.

Построим графики уравнений регрессии на одном чертеже с эмпирическими линиями регрессии:

б) Выборочный коэффициент корреляции вычислим по формуле:

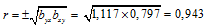
По шкале Чеддока связь прямая, очень сильная.

На уровне α=0,05 оценим его значимость. Для этого вычислим статистику критерия:

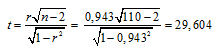
Для уровня значимости α=0,05 и числа степеней свободы k=110-2=108 находим критическое значение статистики t_0,95;108=1,98. Поскольку |t|> t_0,95;108, следовательно, коэффициент корреляции между водопоглощением Y и содержанием нефтешламов в материалах X значимо отличается от нуля.

в) используя уравнение регрессии , оценим средний процент водопоглощения в образцах, содержащих 35 % нефтешламов:

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---