Задачи-онлайн с решением по Теории вероятностей

Тема: Задачи-онлайн с решением по Теории вероятностей

Раздел: Бесплатные рефераты по теории вероятностей и математической статистике

Тип: Задача | Размер: 46.22K | Скачано: 316 | Добавлен 16.03.17 в 16:27 | Рейтинг: 0 | Еще Задачи

Задача 1. Студент забыл шифр своего кейса. Какова вероятность открыть кейс с первой попытки, если студент помнит, что нулей и семёрок нет, а все три цифры различны?

Решение.

Шифр может содержать любые три из 8-и цифр (1, 2, 3, 4, 5, 6, 8 и 9). Поскольку при наборе шифра важен не только состав набираемых цифр, но и порядок набора, то общее число различных вариантов шифра равно числу размещений из 8-и элементов по 3 элемента:

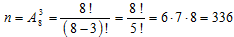
Событию A – кейс будет открыт с первой попытки – благоприятствует только одна определённая комбинация:

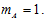
По классическому определению вероятности, вероятность события А:

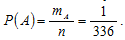
Ответ: вероятность открыть кейс с первой попытки равна 1/336.

 

Задача 2. Число проезжающих по автостраде легковых автомобилей относится к числу грузовых как 5:3. Каждая 20-я легковая машина заправляется у расположенной при автостраде бензоколонки. Из грузовиков в заправке нуждается только один из ста. Наугад взятая машина подъехала для заправки. С какой вероятностью это грузовая машина?

Решение.

Пусть событие A – случайно выбранная машина заправится у бензоколонки.

Выдвинем гипотезы:

H₁ – случайно выбрана легковая машина;

H₂ – случайно выбрана грузовая машина.

Найдём вероятности гипотез. Пусть за некоторое время по шоссе около бензоколонки проехало 5k легковых машин. Следовательно, грузовых за это же время проехало 3k. Тогда по классическому определению вероятности имеем:

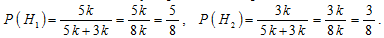
Условные вероятности события A найдём также по статистическому определению вероятности:

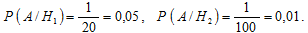
Вероятность события A определим по формуле полной вероятности:

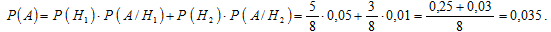
Нам надо найти условную вероятность гипотезы H₂. Используем формулу Байеса:

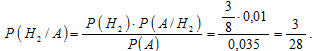
Ответ: вероятность того, что для заправки подъехала грузовая машина, равна 3/28.

 

Задача 3. В среднем 20 % пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене будет продано менее 2 пакетов.

Решение.

Используя статистическое определение вероятности, вероятность продажи пакета акций по первоначально заявленной цене  можно считать одинаковой для всех пакетов. Тогда продажу  пакетов акций можно рассматривать как повторные независимые испытания. Следовательно, вероятность того, что в результате торгов по первоначально заявленной цене будет продано ровно  пакетов, будет определяться по формуле Бернулли:

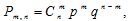
где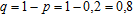  

– вероятность того, что случайно выбранный пакет акций не будет продан по первоначально заявленной цене.

Найдём вероятность того, что из -и пакетов акций в результате торгов по первоначально заявленной цене будет продано менее 2 пакетов:

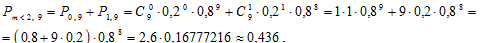
Ответ: вероятность того, что из 9-и пакетов акций в результате торгов по первоначально заявленной цене будет продано менее 2 пакетов, равна 0,436.

 

Задача 4. Вероятность заболевания бешенством бродячих собак равна 0,4. Какова вероятность, что среди 50 собак будет 30 заболевших?

Решение.

Данная задача соответствует условиям испытаний Бернулли с параметрами:

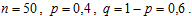
Точная вероятность того, что из - n=50 и собак ровно m = 30 заболеют бешенством, вычисляется по формуле Бернулли:

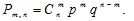
Однако из-за больших значений n и m удобнее использовать приближённые формулы. В данной задаче 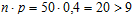, поэтому вероятность найдём, используя локальную теорему Муавра-Лапласа:

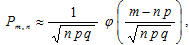
где 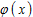 – плотность распределения нормированной нормальной случайной величины.

Подставляя данные задачи, получим:

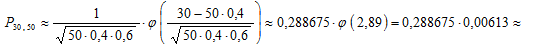
Ответ: вероятность того, что среди 50 собак будет 30 заболевших, приближённо равна 0,0018.

 

Задача 5. Вероятность попадания хотя бы один раз при четырёх выстрелах равна 0,9375. Чему равна вероятность попадания при одном выстреле?

Решение.

Пусть событие A_i – промах при i-м выстреле, i = 1, 2, 3, 4. Вероятность этих событий одинакова:

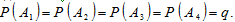
Вероятность события B – ни одного попадания при 4-х выстрелах – по теореме о вероятности произведения независимых событий равна:

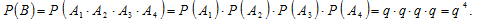
Нам известна вероятность события  (хотя бы одно попадание в цель при четырёх выстрелах):

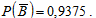
С другой стороны:

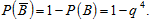
То есть:

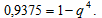
Отсюда находим вероятность промаха:

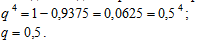
Следовательно, вероятность попадания в цель при одном выстреле:

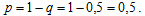
Ответ: вероятность попадания в цель при одном выстреле равна 0,5.

 

Задача 6. В студенческой группе 15 девушек и 10 юношей. Наугад выбирают делегацию из трёх человек. Какова вероятность того, что среди них две девушки?

Решение.

Всего имеется 15 + 10 = 25 человек. Число различных способов, которыми можно выбрать 3-х человек из 25-и, равно числу сочетаний из 25-и элементов по 3 элемента:

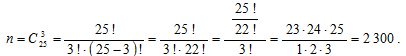
Пусть событие A состоит в том, что в комиссию попадут две девушки.

Чтобы произошло событие A, 2 члена комиссии должны быть выбраны из числа 15-и девушек ( способов выбора), а оставшийся третий член комиссии – из числа 10-и юношей ( способов выбора).

По правилу произведения в комбинаторике, число способов выбора комиссии, благоприятствующих событию A, равно:

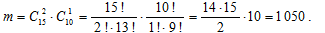
По классическому определению вероятности находим искомую вероятность:

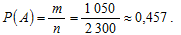
Ответ: вероятность того, что в комиссию попадут две девушки, равна 0,457.

 

Задача 7. Для первой машинистки вероятность допустить опечатку на странице равна 0,03, а для второй – 0,12. Вторая работает в полтора раза быстрее первой. Отпечатанные страницы кладываются в общую пачку. Наугад взята одна страница. Какова вероятность того, что она содержит опечатку?

Решение.

Пусть событие A – случайно взятая из общей пачки страница содержит опечатку.

Выдвинем гипотезы:

H₁ – страница набрана первой машинисткой;

H₂ – страница набрана второй машинисткой.

Найдём вероятности гипотез. Пусть за некоторое время первая машинистка набрала 2k страниц. Согласно пропорции, втора машинистка за это же время наберёт 3k страниц. Тогда по классическому определению вероятности имеем:

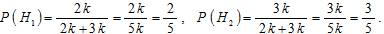
Условные вероятности события A известны:

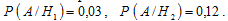
Вероятность события A определим по формуле полной вероятности:

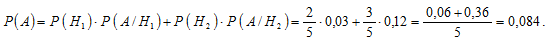
Ответ: вероятность того, что случайно взятая из общей пачки страница содержит опечатку, равна 0,084.

 

Задача 8. Найти вероятность того, что при 100 бросаниях монеты будет:

а) ровно 25 гербов;

б) не менее 25 гербов.

Решение.

Мы находимся в схеме Бернулли с параметрами:

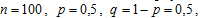
где p – вероятность выпадения герба при одном подбрасывании монеты.

Поскольку в данном случае 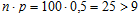, то для вычисления заданных вероятностей используем приближённые формулы Муавра-Лапласа.

а) Найдём вероятность того, что при ста бросаниях монеты выпадет ровно m = 25 гербов, с помощью локальной теоремы Муавра-Лапласа:

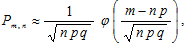
где 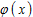  – плотность распределения нормальной нормированной случайной величины;

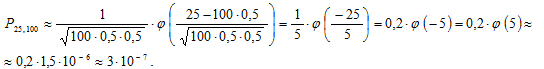
б) Найдём вероятность того, что при ста бросаниях монеты выпадет не менее 25 гербов, то есть от m₁ = 25 до m₂ = 100 гербов, с помощью интегральной теоремы Муавра-Лапласа:

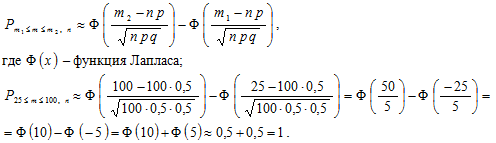
Ответ:

а) вероятность того, что при 100 бросаниях монеты будет ровно 25 гербов, приближённо равна ;

б) вероятность того, что при 100 бросаниях монеты будет не менее 25 гербов, приближённо равна 1.

 

Задача 9. В среднем из 100 человек 2 опаздывают на поезд. На поезд продано 815 билетов. Каково наиболее ожидаемое число опоздавших? Чему равна соответствующая вероятность?

Решение.

По статистическому определению вероятности, вероятность того, что случайно выбранный пассажир опоздает на поезд, равна p=0,002 Эту вероятность можно считать одинаковой для всех пассажиров. Тогда посадка  пассажиров может считаться испытаниями Бернулли. Следовательно, вероятность того, что из n=815 -и пассажиров ровно m  опоздают, будет находиться по формуле Бернулли:

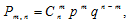
где 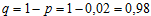 – вероятность того, что случайно выбранный пассажир не опоздает на поезд.

Наивероятнейшее число m0 опоздавших пассажиров находится из неравенства

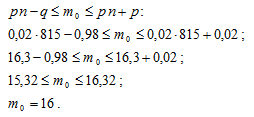
Поскольку n велико, то нахождение вероятностей по формуле Бернулли будет связано с большим объёмом вычислений. Для упрощения вычислений используем одну из приближённых формул.

В данном случае 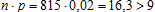, поэтому для нахождения вероятности опоздания ровно m0=16 - и пассажиров используем локальную теорему Муавра-Лапласа:

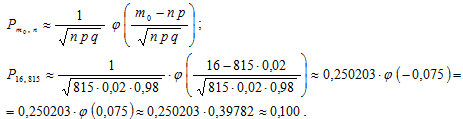
Ответ:

наиболее ожидаемое число опоздавших пассажиров – 16 человек;

вероятность того, что на поезд опоздает 16 человек, приближённо равна 0,100.

 

Задача 10. Три стрелка стреляют по мишени. Первый попадает с вероятностью 0,9, второй  вероятностью 0,7 и третий с вероятностью 0,4. Найти вероятность того, что при одном залпе в мишень попадёт:

а) только один стрелок;

б) хотя бы один стрелок.

Решение.

Обозначим элементарные события:

A1 – первый стрелок попал в мишень;

A2 – второй стрелок попал в мишень;

A3 – третий стрелок попал в мишень.

Вероятности событий Ai известны:

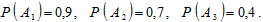
Найдём вероятности обратных событий 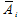 (промахов):

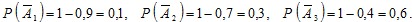
а) Пусть событие A состоит в том, что при залпе трёх стрелков будет ровно одно попадание.

Событие A можно описать через элементарные события следующим образом:

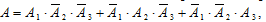
то есть попадёт или только 1-й стрелок (событие 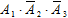), или только 2-й стрелок (событие ), или только 3-й стрелок (событие ).

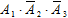По теореме о вероятности суммы несовместных событий имеем:

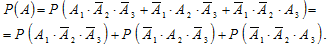
По теореме о вероятности произведения независимых событий окончательно получаем:

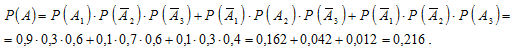
б) Пусть событие  состоит в том, что при залпе трёх стрелков не будет ни одного попадания.

Событие  можно описать через элементарные события следующим образом:

B=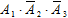

По теореме о вероятности произведения независимых событий:

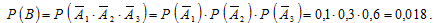
Тогда искомая вероятность события «хотя бы одно попадание в мишень при залпе трёх стрелков» (событие B):

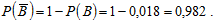
Ответ:

а) вероятность того, что при залпе трёх стрелков будет одно попадание, равна 0,216;

б) вероятность того, что при залпе трёх стрелков будет хотя бы одно попадание в мишень, равна 0,982.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---