Контрольная по Высшей математике Вариант № 6

Тема: Контрольная по Высшей математике Вариант № 6

Раздел: Бесплатные рефераты по высшей математике

Тип: Контрольная работа | Размер: 301.73K | Скачано: 326 | Добавлен 20.02.17 в 17:04 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Финансовый университет при правительстве РФ. Барнаулский филиал.

1) Даны две матрицы А и В. Найти:

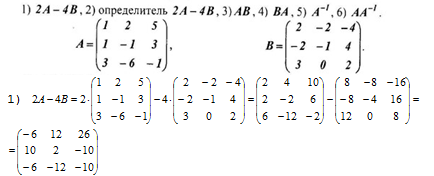
2) Определитель:

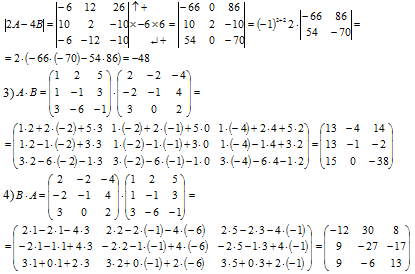
5) Определитель матрицы:

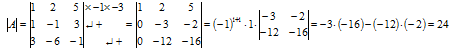
Алгебраические дополнения матрицы А:

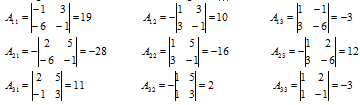
Транспонированная матрица алгебраических дополнений:

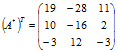
Обратная матрица: 

 

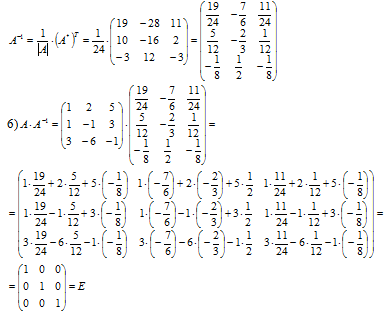
2) Решите систему линейных  уравнений.

2.1 Методом Крамера.

2.2 Матричном способом ( с помощью А-1).

2.3 Методом Гаусса.

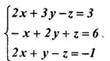
2.1.Определители:

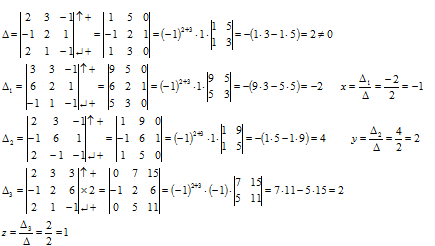
Решение системы:

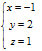
Проверка:

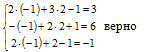
2.2. Матричное уравнение, соответствующее системе: A*X=B , где

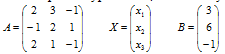
Решение матричного уравнения:

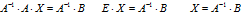
Определитель матрицы:

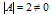
Алгебраические дополнения матрицы А:

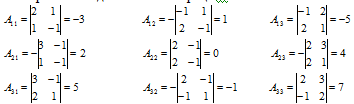
Транспонированная матрица алгебраических дополнений:

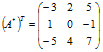
Обратная матрица: 

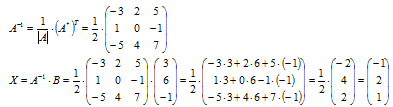
Решение системы:

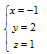
2.3. Приведение расширенной матрицы системы к ступенчатому виду: 

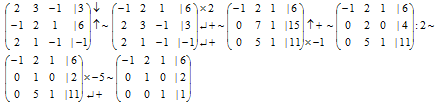
Ранг матрицы 3 (число ненулевых строк), ранг  расширенной матрицы 3, число неизвестных 3, решение единственное.

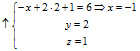
Решение системы:

 

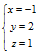
3) Вычислить искомый результат и вставить его вместо многоточия.

Векторное произведение векторов a и b равно (2; 0; -1). Тогда вектор 

с = -2b × 3a будет иметь координаты …
Векторное произведение: 

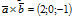
Вектор:

 

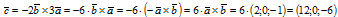
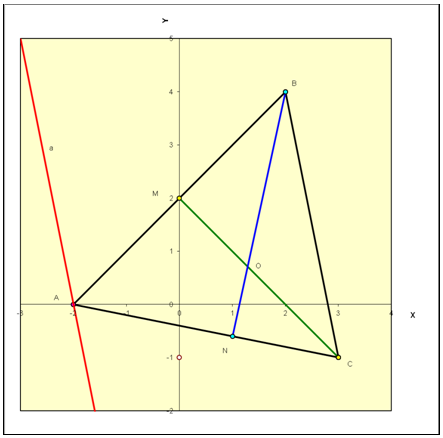
4) Даны координаты вершин треугольника ABC. Найти:

4.1 Уравнение стороны AB.

4.2 Уравнение высоты BN, проведенной из точки B.

4.3 Длину высоты BN.

4.4 Уравнение медианы, проведенной из точки С.

4.5 Координаты точки O пересечения медианы С и высоты ВN.

4.6 Уравнение прямой, проходящий через вершину А параллельно стороне ВС.
А(-2 ; 0 ), B( 2 ; 4 ), C( 3 ; -1 ).
1.1. Уравнение прямой АВ: 

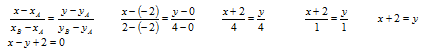
1.2. Угловой коэффициент прямой АC:

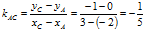
Угловой коэффициент прямой BN   по условию перпендикулярности прямых AC и BN:

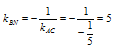
Уравнение высоты – прямой BN: 

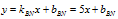
Для точки В, принадлежащей прямой BN:  

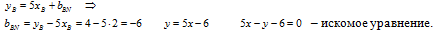
1.3. Уравнение прямой АС: 

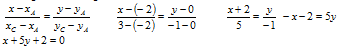
Расстояние от точки В до прямой АС – длина отрезка BN: 

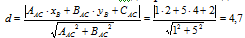
1.4. Координаты точки М – середины отрезка АВ:

Уравнение медианы –  прямой СМ: 

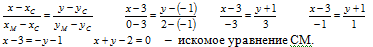
1.5. Координаты точки О – пересечения прямых СМ и BN: 

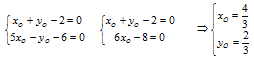
1.6. Угловой коэффициент прямой ВC:

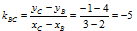
По условию параллельности прямых ВС и а, уравнение прямой a: 

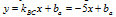
Для точки А, принадлежащей прямой а:  

– искомое уравнение.

Чертеж:

 

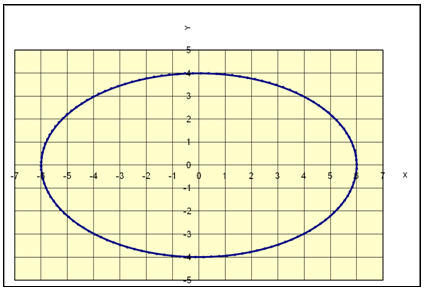
5) Дана кривая, уравнение который имеет вид

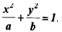
Определить тип кривой. Найти координаты  и фокусов, эксцентриситет. Построит рисунок.
a =36, b =16.

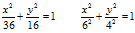– каноническое уравнение эллипса с полуосями

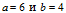и центром симметрии (0;0).

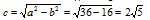
Координаты фокусов:

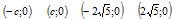
Эксцентриситет:

 

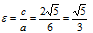
6) Вычислить пределы функций.

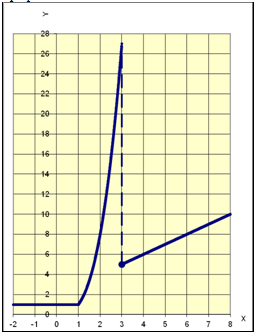
7) Исследовать на непрерывность, найти точки разрыва функции, указать характер разрыва, изобразить графически

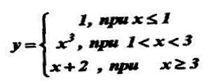
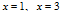– точки, подозрительные на разрыв;

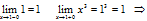
в точке x=1  разрыва нет.

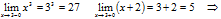
в точке x=3 разрыв 1-го рода (скачок функции).

График:

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---