Контрольная работа по Теории вероятностей Вариант 3

Тема: Контрольная работа по Теории вероятностей Вариант 3

Раздел: Бесплатные рефераты по теории вероятностей и математической статистике

Тип: Контрольная работа | Размер: 112.18K | Скачано: 286 | Добавлен 17.02.17 в 16:42 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Новосибирский государственный университет экономики и управления

Год и город: Новосибирск 2016

Ситуационная (практическая) задача № 1

Время ξ ожидания заправки автомашины на АЗС города N является случайным с плотностью распределения

• Установить неизвестную постоянную С и построить график функции p(x)
• Найти функцию распределения случайной величин ξ и построить ее график
• Вычислить математическое ожидание (среднее значение), дисперсию и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины
• Во сколько раз число автомашин, ожидающих заправку меньше среднего времени, превышает число автомашин, ожидающих заправку больше среднего времени?

Решение:

1) Учитывая свойства плотности распределения  р(x): 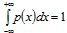, имеем

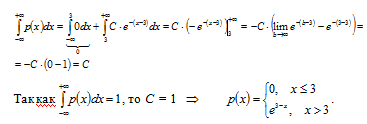
Построим график функции :

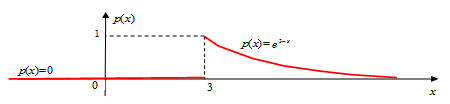
2) Функцию распределения F(х) находим за формулой: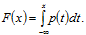

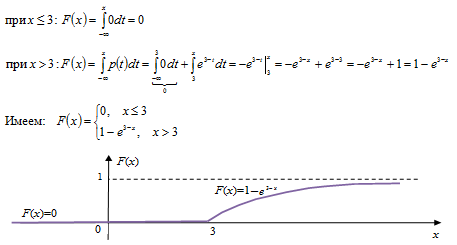
3)  Для непрерывных случайных величин математическое ожидания (среднее значение) находится по формуле:

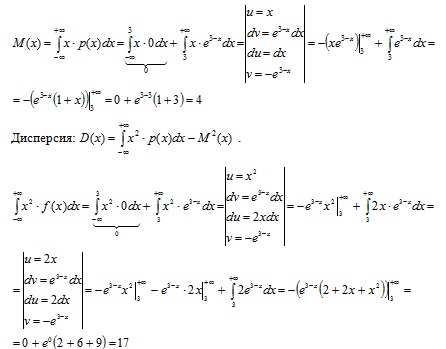
Тогда дисперсия:

Среднее квадратичное  отклонение – это корень квадратный из дисперсии:

4) Найдем, во сколько раз число автомашин, ожидающих заправку меньше среднего времени (4 минуты), превышает число автомашин, ожидающих заправку больше среднего времени, т.е. найдем, во сколько раз вероятность ожидать заправку меньше 4 минут больше вероятности ожидать заправку больше 4 минут.

Для х < 4:

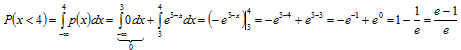
Для х > 4:

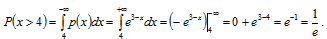
Находим отношение этих величин:

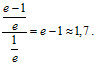
Ответ: 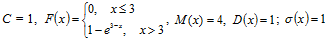   , в 1,7 раза.

 

 

Ситуационная (практическая) задача № 2

База снабжает 5 магазинов, от каждого из которых в течение суток может поступить заявка на поставку товара с вероятностью 0,7. Составить ряд и функцию распределения числа поступивших за сутки заявок от магазинов и представить их графически.

Решение:

Случайная величина  Х – число поступивших за сутки заявок от магазинов – может принимать одно из 6-ти значений:   х = 0,1,2,3,4,5. Найдем вероятность каждого из этих значений.

Используем формулу Бернулли:

Если проводится n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, то вероятность того, что событие А настанет ровно k раз, равняется

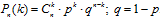
Вероятность поступления заявки равна 0,7, то есть       

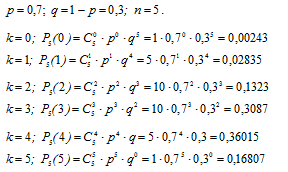
Составляем таблицу (биномиальный закон  распределения), записывая значения х_і = k, которые может принимать дискpетная случайная величина Х, а также вероятности p_і = Р₅(x_і) = Р₅(k).

Х	xі	0	1	2	3	4	5
	pі	0,00243	0,02835	0,1323	0,3087	0,36015	0,16807

Проверка: сумма всех вероятностей должна быть = 1:

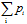=0,00243+ 0,02835+ 0,1323+ 0,3087 +0,36015+0,16807 =1

Построим многоугольник распределения:

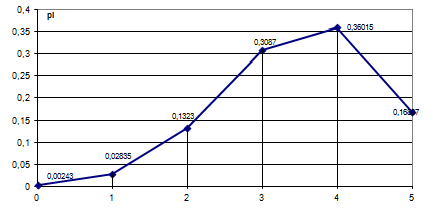
Построим функцию распределения.

Так как  Х – дискретная случайная величина, то функция распределения

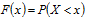– кусочно-постоянная функция:

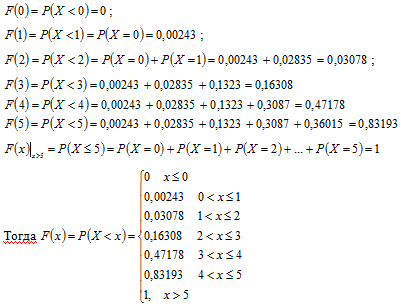
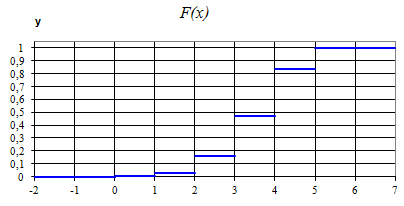
Ответ:

Х	xі	0	1	2	3	4	5
	pі	0,00243	0,02835	0,1323	0,3087	0,36015	0,16807

 

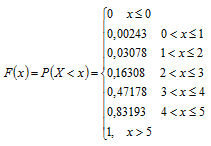
Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. У сборщика имеется 10 новых и 5 бывших в употреблении (б/у) деталей, которые мало отличаются друг от друга по внешнему виду. Сборщик наудачу берет три детали. Найти вероятность того, что среди них будет только одна деталь б/у.

А. 0,011

Б. 0,4945

В. 0,978

Г. 0,2

 

2. Экспедиция издательства отправляет газеты в три почтовых отделения. Известно, что в первое отделение газеты доставляются своевременно в среднем в 92% всех случаев, во второе – 80%, в третье – 76%. Найти вероятность, что из трех почтовых отделений хотя бы одно получит вовремя.

А. 0,559

Б. 0,9962

В. 0,0038

Г. 0,92

 

3. В ящике 15 теннисных мячей, из которых 11 новых. Для первой игры наудачу берут три мяча, которые после игры возвращают в ящик. Для второй игры также наудачу берут из ящика три мяча. Определить вероятность того, что все три мяча, взятые для второй игры, будут новыми.

А. 0,1753

Б. 0,363

В. 0,264

Г. 0,9247

 

4. В торговую фирму поступили телевизоры от трех поставщиков в соотношении 2:1:2. Практика показала, что телевизоры, поступающие от первого, второго и третьего поставщиков, не требуют ремонта в течение гарантийного срока в среднем соответственно в 80%, 90%, 85% случаев. Проданный телевизор не потребовал ремонта в течение гарантийного срока. Определить вероятность того, что он поступил от первого поставщика?

А. 0,32

Б. 0,381

В. 0,84

Г. 0,8

 

5. По результатам проверок налоговыми инспекциями установлено, что в городе N в среднем 25% малых предприятий нарушают финансовую дисциплину. Какова вероятность того, что из шести малых предприятий города N нарушения финансовой дисциплины будут иметь ровно два?

А. 0,2222

Б. 0,2966

В. 0,7234

Г. 0,25

 

6. В результате проверки качества приготовленных для посева семян огурца установлено, что в среднем 68% семян всхожи. Какова вероятность, что из посеянных семи семян взойдут хотя бы два?

А. 0,0055

Б. 0,9945

В. 0,962

Г. 0,038

 

7. Из-за болезни на работу ежедневно не выходит в среднем 4% работников предприятия. Какова вероятность того, что из 200 работников, выбранных наудачу из списочного состава предприятия, на работе будет отсутствовать не более 10 сотрудников предприятия?

А. 0,002

Б. 0,7628

В. 0,7648

Г. 0,2648

 

8. Некоторая страховая компания выплачивает страховую сумму в среднем по 6% договоров. Сколько нужно застраховать клиентов, чтобы с вероятностью 0,94 можно было утверждать, что доля получивших страховую сумму среди них отклонится по абсолютной величине от вероятности получения каждым клиентом страховой суммы не более, чем на 0,03?

А. 15

Б. 222

В. 4

Г. 94

 

9. Студент знает 20 из имеющихся 30 вопросов программы по теории вероятностей. Экзаменационный билет содержит четыре произвольных вопроса программы. Студент получает на экзамене отличную оценку («пять»), если он знает все вопросы билета; хорошую оценку («четыре»), если знает три вопроса; удовлетворительную оценку («три»), если знает два вопроса; в остальных случаях он получает неудовлетворительную оценку («два»). Найти математическое ожидание и дисперсию оценки, полученной студентом на экзамене.

А. Mξ=3,674;Dξ=0,764

Б. Mξ=2,674;Dξ=0,764

В. Mξ=3,674;Dξ=10,59

Г. Mξ=3,674;Dξ=14,26

 

10. Охотник, имеющий четыре патрона, стреляет по цели до тех пор, пока не попадет или не израсходует все патроны. Известно, что в цель данного вида он попадает в среднем 7 раз из 10 выстрелов. Рассматривается случайная величина ξ - число израсходованных охотником патронов. Найти P(ξ>Mξ+1)

А. 0,09

Б. 0,3

В. 0,91

Г. 0,7

 

Библиографический список

1. Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика : учеб. пособие для вузов / В. Е. Гмурман .- 9-е изд.,стер .- М. : Высш. шк., 2003 .- 478, [1] с. (МОРФ)
2. Гмурман, Владимир Ефимович. Руководство к решению задач по теории вероятностей и математической статистике : учеб. пособие для вузов / В. Е. Гмурман .- 11-е изд., перераб .- М. : Высш. образование, 2007 .- 404 с.
3. Высшая математика для экономистов : учеб. для вузов по экон. специальностям / [Н. Ш. Кремер и др.] ; под ред. Н. Ш. Кремера .- 3-е изд.- М. : ЮНИТИ, 2009 .- 478, [1] с. (МОРФ)
4. Кремер, Наум Шевелевич. Теория вероятностей и математическая статистика : Учеб. для вузов по экон. спец. / Кремер Н. Ш.; [ВЗФЭИ] .- М. : ЮНИТИ, 2000 .- 543 с.: ил.
5. Бородин, Андрей Николаевич. Элементарный курс теории вероятностей и математической статистики : учеб. пособие для вузов по немат. специальностям / А. Н. Бородин .- 7-е изд., стер .- СПб. [и др.] : Лань, 2008 .- 254 с
6. Теория вероятностей и математическая статистика : учеб. пособие для вузов по направлению "Экономика" и др. экон. специальностям / [Л. Г. Бирюкова и др.] ; под ред. В. И. Ермакова ; Рос. экон. акад. им. Г. В. Плеханова .- М. : ИНФРА-М, 2010 .- 286 с.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---