Онлайн задачи по Методам оптимальных решений

Тема: Онлайн задачи по Методам оптимальных решений

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Задача | Размер: 530.14K | Скачано: 196 | Добавлен 13.02.17 в 11:29 | Рейтинг: 0 | Еще Задачи

Задание 1.10

Решить задачи с использованием графического метода:

L(¯x)=x_1+x_2→min при ограничениях

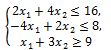
x_1≥0,x_2≥0

Решение

Построим область определения этой задачи. Ограничения x_1,x_2≥0 задают первую координатную четверть плоскости х1Ох2.

Для получения решения графическим методом строим прямые:

I 2x_1+4x_2≤16. Прямая проходит через точки (8; 0) и (0; 4). Для нахождения полуплоскости, соответствующей данному неравенству, берем любую точку, не лежащую на граничной прямой, и подставляем ее координаты в неравенство. Возьмем точку О(0;0): 2*0 + 4*0 ≤ 16, 0≤16 Неравенство выполняется, значит, исходному неравенству соответствует та полуплоскость, которая содержит точку О (0;0).

II -4x_1+2x_2≤8. Прямая проходит через точки (-2; 0) и (0; 4). Возьмем точку О(0;0): -4*0 + 2*0 ≤ 8, 0≤8 Неравенство выполняется, значит, исходному неравенству соответствует та полуплоскость, которая содержит точку О (0;0).

III x_1+3x_2≥9. Прямая проходит через точки (9; 0) и (0; 3). Возьмем точку О(0;0): 0 + 3*0 ≥9, 0≥9. Неравенство не выполняется, значит, исходному неравенству соответствует та полуплоскость, которая не содержит точку О (0;0).

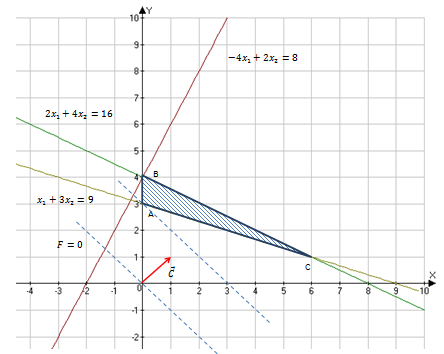
Рис. 1. Графический метод решения задачи

Решением является замкнутый многоугольник ABC. Любая точка этого многоугольника внутри и на границе является решением или рекомендацией допустимой задачи.

Строим вектор C ⃗=(c_1;c_2)=(1; 1). Перпендикулярно к вектору C ⃗ проводим линию уровня F=0.

Параллельным перемещением прямой F=0 вдоль вектора C ⃗ находим крайнюю точку A, в которой целевая функция принимает минимальное значение.

Координаты точки A определяются системой

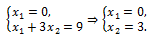
Откуда Z_min (0;3)=1∙0+1∙3=3

Ответ: Z_min (0;3)=3

 

Задание 2.8

Решить задачи симплексным методом:

L(¯x)=3x_1+x_2+2x_3→min при ограничениях

x_j≥0,j=1,2,3.

Решение

Введем искусственные переменные. В 1 равенстве вводим переменную x_4. Во 2 равенстве вводим переменную x_5.

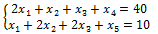
Целью решения вспомогательной задачи является получение допустимого базисного решения не содержащего искусственных переменных (x_4, x_5). Для этого сформируем вспомогательную целевую функцию:

Z=x_4+x_5

и проведем ее минимизацию в заданной системе ограничений. Если после минимизации функции Z ее оптимальное значение будет равно нулю и все искусственные переменные окажутся выведенными из базиса, то полученное базисное решение есть допустимое базисное решение исходной задачи. Если же после минимизации функции Z ее оптимальное значение окажется отличным от нуля, значит исходная система ограничений противоречива (область допустимых решений пуста) и исходная задача решения не имеет.

Для решения вспомогательной задачи симплекс-методом выразим функцию Z через свободные переменные, для этого: вычтем из функции Z уравнение 1 и уравнение 2.

Функция Z примет вид :

Z=-3x_1-3x_2-3x_3+50

Сформируем начальную симплекс-таблицу.

БП	x_1	x_2	x_3	x_4	x_5	Решение	Отношение
x_4	2	1	1	1	0	40	40/1=40
x_5	1	2	2	0	1	10	10/2=5
L	3	1	2	0	0	0
Z	-3	3	-3	0	0	-50

Разрешающий столбец – x_3, разрешающая строка – x_5

Итерация 1

БП	x_1	x_2	x_3	x_4	x_5	Решение	Отношение
x_4	3/2	0	0	1	0	35	35: 3/2=70/3
x_5	1/2	1	1	0	1	5	5: 1/2=10
L	2	-1	0	0	0	-10
Z	-3/2	0	0	0	0	-35

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в строке L есть положительные элементы, то полученное решение не оптимально.
Разрешающий столбец – x_1, разрешающая строка – x_3

Итерация 2

БП	x_1	x_2	x_3	x_4	x_5	Решение
x_4	0	-3	-3	1	0	20
x_1	1	2	2	0	1	10
L	0	-5	-4	0	0	-30
Z	0	3	3	0	0	-20

 Получено оптимальное решение вспомогательной задачи (найден минимум функции Z т.к. в строке функции нет отрицательных коэффициентов). Значение функции Z положительно и в базисе имеются искусственные переменные, поэтому исходная задача неразрешима из-за противоречивости системы ограничений.

Ответ: нет решений.

 

Задание 2.9

Решить симплекс-методом

L(¯x)=x_1+x_2+x_3+x_4→min при ограничениях

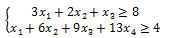
x_j≥0,j=1,2,3,4.

Решение

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1 неравенстве вводим базисную переменную x_5. Во 2 неравенстве вводим базисную переменную x_6. Так как в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные.

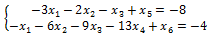
Сформируем начальную симплекс-таблицу.

БП	x_1	x_2	x_3	x_4	x_5	x_6	Решение	Отношение
x_5	-3	-2	-1	0	1	0	-8	(-8)/(-3)=8/3
x_6	-1	-6	-9	-13	0	1	-4	(-4)/(-1)=4
F	1	1	1	1	0	0	0

Разрешающий столбец – x_1, разрешающая строка – x_5

Итерация 1

БП	x_1	x_2	x_3	x_4	x_5	x_6	Решение	Отношение
x_1	1	2/3	1/3	0	-1/3	0	8/3	-
x_6	0	-16/3	-26/3	-13	-1/3	1	-4/3	-13:(-4/3)=39/4
F	0	1/3	2/3	1	1/3	0	-8/3

Так как среди свободных членов есть отрицательные значения, то решение недопустимое и сначала нужно перейти к допустимому решению.

Разрешающий столбец – x_4, разрешающая строка – x_6

Итерация 2

БП	x_1	x_2	x_3	x_4	x_5	x_6	Решение	Отношение
x_1	1	2/3	1/3	0	-1/3	0	8/3	8/3:2/3=4
x_4	0	16/39	2/3	1	1/39	-1/13	4/39	4/39:16/39=1/4
F	0	-1/13	0	0	4/13	1/13	-36/13

Данное решение не оптимально.

Разрешающий столбец – x_2, разрешающая строка – x_4

Итерация 3

БП	x_1	x_2	x_3	x_4	x_5	x_6	Решение	Отношение
x_1	1	0	-3/4	-13/8	-3/8	1/8	5/2	8/3:2/3=4
x_2	0	1	13/8	39/16	1/16	-3/16	1/4	4/39:16/39=1/4
F	0	0	1/8	3/16	5/16	1/16	-11/4

Последняя строка не содержит отрицательные элементы. Поэтому эта таблица определяет оптимальный план задачи.

Оптимальный план: x_1=5/2,x_2=1/4,x_3=0,x_4=0

Z_min (5/2,1/4,0,0)=5/2+1/4=11/4

Ответ: Z_min (5/2,1/4,0,0)=11/4 

 

Задание 3.2

Решить транспортную задачу

a_i \ b_j	70	30	20	40
90	1	3	4	5
30	5	3	1	2
40	2	1	4	2

Решение

Данная задача является закрытой, так как запасы поставщиков 90+30+40=160 и потребности 70+30+20+40=160 совпадают.

Теперь исходные данные задачи запишем в виде таблицы, а опорный план получим методом северо-западного угла.

Получим следующую таблицу.

a_i \ b_j	b1=70	b2=30	b3=20	b4=40
a1=90	1     70	3     20	4	5     0	α1=0
a2=30	5	3     10	1     20	2	α2=0
a3=40	2	1	4	2     40	α3=-3
	β1=1	β2=3	β3=1	β4=5

Число заполненных клеток равно 6 и m+n-1=3+4-1=6 – план невырожденный. Оптимальный план найдём методом потенциалов.

Стоимость этого плана равна:

L=1*70+3*20+3*10+1*20+5*0+2*40 = 260.

Расставим потенциалы:

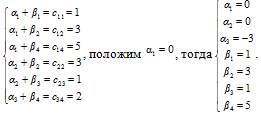
(Обычно равным нулю принимают потенциал строки или столбца с наибольшим числом заполненных клеток.)

Теперь проверим пустые клетки на выполнение неравенства

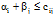
Для клетки (2,4) неравенство не выполняется, значит опорный план не является оптимальным. В эту клетку нужно "ввезти" груз. Строим цикл.

Цикл перерасчёта таблицы – это последовательность ячеек, начинающаяся и заканчивающаяся в одной и той же клетке, с вершинами, лежащими в занятых клетках, кроме одной.

Вершина цикла – клетка, в которой происходит поворот под прямым углом.

"Перемещаем" груз по следующим правилам:

каждой из клеток, связанных циклом присваивается знак: пустой ячейке "+", остальным - поочерёдно знаки "-" и "+" .

среди минусовых клеток находим число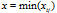  

и прибавляем его к числам, стоящим в плюсовых клетках, и вычитаем из чисел, стоящих в минусовых клетках; остальные клетки вне цикла остаются без изменения.

В нашем примере цикл образуют четыре ячейки: (2,4) – пустая, для которой не выполняется неравенство, и (2,2), (1,2), (1,4) – заполненные.

a_i \ b_j	b1=70	b2=30	b3=20	b4=40
a1=90	1     70	3   +   20	4	5   –   0	α1=0
a2=30	5	3   –   10	1     20	2   +	α2=0
a3=40	2	1	4	2     40	α3=-3
	β1=1	β2=3	β3=1	β4=5

х = min(10, 0)= 0. Значит в плюсовые клетки "завозим" 0 ед. груза, из минусовых "вывозим". Получим новый опорный план:

a_i \ b_j	b1=70	b2=30	b3=20	b4=40
a1=90	1     70	3     20	4	5	α1=0
a2=30	5	3     10	1     20	2     0	α2=0
a3=40	2	1	4	2     40	α3=0
	β1=1	β2=3	β3=1	β4=2

Расставим потенциалы и проверим пустые клетки на выполнение неравенства 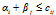 . Для клетки (3,2) неравенство не выполняется. Строим новый цикл.

a_i \ b_j	b1=70	b2=30	b3=20	b4=40
a1=90	1     70	3     20	4	5	α1=0
a2=30	5	3   –   10	1     20	2   +   0	α2=0
a3=40	2	1   +	4	2   –   40	α3=0
	β1=1	β2=3	β3=1	β4=2

х = min(10,40)=10. Значит в плюсовые клетки "завозим" 10 ед. груза, из минусовых "вывозим". Получим новый опорный план:

a_i \ b_j	b1=70	b2=30	b3=20	b4=40
a1=90	1     70	3     20	4	5	α1=0
a2=30	5	3	1     20	2     10	α2=-2
a3=40	2	1     10	4	2     30	α3=-2
	β1=1	β2=3	β3=3	β4=4

Расставим потенциалы и проверим пустые клетки на выполнение неравенства .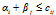

Полученный план является оптимальным.

Стоимость этого плана равна:

L=1*70+3*20+1*20+2*10+1*10+2*30 = 240.

Анализ оптимального плана.

От 1 поставщика нужно поставить 70 ед. груза 1-му потребителю и 20 ед. груза 2-му потребителю.

От 2 поставщика нужно поставить 20 ед. груза 3-му потребителю и 10 ед. груза 4-му потребителю.

От 3 поставщика нужно поставить 10 ед. груза 2-му потребителю и 30 ед. груза 4-му потребителю.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Задачи на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Задачи для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Задача, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---