Контрольная работа по Методам оптимизации решений Вариант №4

Тема: Контрольная работа по Методам оптимизации решений Вариант №4

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 388.11K | Скачано: 257 | Добавлен 08.02.17 в 11:24 | Рейтинг: 0 | Еще Контрольные работы

1. Сущность симплекс-метода.

Симплекс-метод - алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве.

Сущность метода: построение базисных решений, на которых монотонно убывает линейный функционал, до ситуации, когда выполняются необходимые условия локальной оптимальности.

Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.

Симплекс-метод делится на однофазный и двухфазный:

1) нахождение исходной вершины множества допустимых решений;

2) последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.

 

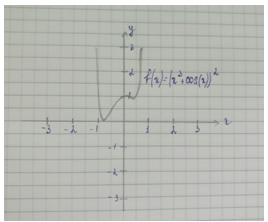
2. Исследовать функцию f(x), найти отрезок, на котором локализован один минимум. Выполнить три итерации для уточнения точки минимума методом «золотого» сечения.

2. x³+cos(x))²

 

3. На станциях отправления сосредоточены запасы однородного груза, который надо перевести в пункты назначения, для каждого из них известна потребность в этом грузе. Задана стоимость перевозки единицы груза из пункта отправления в пункт назначения. Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2	3	3	28
А2	3	3	8	50
А3	3	5	2	39
Потребность в грузе	21	36	60	117

Обозначим суммарный запас груза у всех поставщиков символом «a» , а суммарную потребность в грузе у всех потребителей – символом «b».

Тогда эта задача будет называться закрытой, так как а=b (21+36+60=117).

Составляем опорный план перевозок методом минимального элемента.

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2 (21)	3(7)	3	28
А2	3	3 (29)	8 (21)	50
А3	3	5	2 (39)	39
Потребность в грузе	21	36	60	117

Считаем кол-во базисных клеток по формуле :  m+n-1= 3+3-1=5.

Кол-во базисных клеток в таблице = 5.

Следовательно, план перевозок – невырожденный.

Далее вычисляю потенциалы для плана перевозки.

Пункты	Назначения			U
Отправления	В1	В2	В3
А1	2 (21)	3	3 (7)	0
А2	3	3 (36)	8 (14)	0
А3	3	5	2 (39)	-6
V	2	3	8

Предположим, что U₁ = 0.

Тогда:   u₁ + v₁ = 2; 0 + v₁ = 2; v₁ = 2;
u₁ + v₂ = 3; 0 + v₂ = 3; v₂ = 3;
u₂ + v₂ = 3; 3 + u₂ = 3; u₂ = 0;
u₂ + v₃ = 8; 0 + v₃ = 8; v₃ = 8;
u₃ + v₃ = 2; 8 + u₃ = 2; u₃ = -6.

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij
(1;3): 0 + 8 > 3; ∆₁₃ = 0 + 8 - 3 = 5

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2 (21)	3 (7) (-)	3 (+)	28
А2	3	3 (29) (+)	8 (21) (-)	50
А3	3	5	2 (39)	39
Потребность в грузе	21	36	60

Получаем новый план:

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2 (21)	3	3 (7)	28
А2	3	3 (36)	8 (14)	50
А3	3	5	2 (39)	39
Потребность в грузе	21	36	60

Проверим оптимальность опорного плана:    u₁ + v₁ = 2; 0 + v₁ = 2; v₁ = 2;
u₁ + v₃ = 3; 0 + v₃ = 3; v₃ = 3;
u₂ + v₃ = 8; 3 + u₂ = 8; u₂ = 5;
u₂ + v₂ = 3; 5 + v₂ = 3; v₂ = -2;
u₃ + v₃ = 2; 3 + u₃ = 2; u₃ = -1.

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij
(2;1): 5 + 2 > 3; ∆₂₁ = 5 + 2 - 3 = 4.

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2 (21) (-)	3	3 (7) (+)	28
А2	3 (+)	3 (36)	8 (14) (-)	50
А3	3	5	2 (39)	39
Потребность в грузе	21	36	60

Получаем новый опорный план:

Пункты	Назначения			Запасы груза
Отправления	В1	В2	В3
А1	2 (7)	3	3 (21)	28
А2	3 (14)	3 (36)	8	50
А3	3	5	2 (39)	39
Потребность в грузе	21	36	60

Проверим оптимальность опорного плана:    u₁ + v₁ = 2; 0 + v₁ = 2; v₁ = 2;
u₂ + v₁ = 3; 2 + u₂ = 3; u₂ = 1;
u₂ + v₂ = 3; 1 + v₂ = 3; v₂ = 2;
u₁ + v₃ = 3; 0 + v₃ = 3; v₃ = 3;
u₃ + v₃ = 2; 3 + u₃ = 2; u₃ = -1.

Опорный план является оптимальным.

Минимальные затраты составят: F(x) = 2*7 + 3*21 + 3*14 + 3*36 + 2*39 = 305.

Анализ оптимального плана:
Из 1-го склада необходимо груз направить в 1-й магазин (7), в 3-й магазин (21)
Из 2-го склада необходимо груз направить в 1-й магазин (14), в 2-й магазин (36)
Из 3-го склада необходимо весь груз направить в 3-й магазин.

 

4. Решить по алгоритму Литтла задачу коммивояжера с матрицей.

	1	2	3	4
1	-	9	8	7
2	9	-	6	8
3	8	6	-	14
4	7	8	14	-

Решение:

Возьмем в качестве произвольного маршрута:
X₀ = (1,2);(2,3);(3,4);(4,1).
Тогда F(X₀) = 9 + 6 + 14 + 7 = 36.

Для определения нижней границы множества воспользуемся  приведением матрицы по строкам, для чего необходимо в каждой строке матрицы D найти минимальный элемент.
d_i = min(j) d_ij

ij	1	2	3	4	di
1	-	9	8	7	7
2	9	-	6	8	6
3	8	6	-	14	6
4	7	8	14	-	7

 Затем вычитаем d_i из элементов рассматриваемой строки. Получается:

ij	1	2	3	4
1	-	2	1	0
2	3	-	0	2
3	2	0	-	8
4	0	1	7	-

Находим минимальный элемент в каждом столбце по формуле d_j = min(i) d_ij

ij	1	2	3	4
1	-	2	1	0
2	3	-	0	2
3	2	0	-	8
4	0	1	7	-
d j	0	0	0	0

Вычитаем минимальные элементы и получаем редуцированную матрицу:

ij	1	2	3	4
1	-	2	1	0
2	3	-	0	2
3	2	0	-	8
4	0	1	7	-

Определим нижнюю границу:

H = ∑d_i + ∑d_j
H = 7+6+6+7+0+0+0+0 = 26.

Определяем ребро ветвления и разобьем все множество маршрутов относительно этого ребра на два подмножества (i,j) и (i*,j*).

d(1,4) = 1 + 2 = 3; d(2,3) = 2 + 1 = 3; d(3,2) = 2 + 1 = 3; d(4,1) = 1 + 2 = 3; 

ij	1	2	3	4	di
1	-	2	1	0 (3)	1
2	3	-	0 (3)	2	2
3	2	0 (3)	-	8	2
4	0 (3)	1	7	-	1
dj	2	1	1	2	0

Проводим исключение ребра:

ij	1	2	3	4	di
1	-	2	1	-	1
2	3	-	0	2	0
3	2	0	-	8	0
4	0	1	7	-	0
dj	0	0	0	2	3

H(1*,4*) = 26 + 3 = 29.

Проводим включение ребра и в результате получаем другую сокращенную матрицу, которая после операции приведения имеет вид:

i j	1	2	3	d i
2	3	-	0	0
3	2	0	-	0
4	-	1	7	1
d j	2	0	0	3

Сумма констант приведения сокращенной матрицы:
∑d_i + ∑d_j = 3.
Нижняя граница подмножества (1,4) равна:
H(1,4) = 26 + 3 = 29 ≤ 29. Новая граница Н=29.

Далее определяем ребро ветвления:

i j	1	2	3	d i
2	1	-	0(7)	1
3	0(1)	0(0)	-	0
4	-	0(6)	6	6
d j	1	0	6	0

d(2,3) = 1 + 6 = 7; d(3,1) = 0 + 1 = 1; d(3,2) = 0 + 0 = 0; d(4,2) = 6 + 0 = 6; 
Наибольшая сумма констант приведения равна (1 + 6) = 7 для ребра (2,3), следовательно, множество разбивается на два подмножества (2,3) и (2*,3*).

Проводим исключение ребра (2,3):

i j	1	2	3	d i
2	1	-	-	1
3	0	0	-	0
4	-	0	6	0
d j	0	0	6	7

H(2*,3*) = 29 + 7 = 36.

Проводим включение ребра (2,3). В результате получается сокращенная матрица:

i j	1	2	d i
3	0	-	0
4	-	0	0
d j	0	0	0

Сумма констант приведения сокращенной матрицы:
∑d_i + ∑d_j = 0.
Нижняя граница подмножества (2,3) равна:
H(2,3) = 29 + 0 = 29 ≤ 36.

Поскольку нижняя граница этого подмножества (2,3) меньше, чем подмножества (2*,3*), то ребро (2,3) включаем в маршрут с новой границей H = 29.
В соответствии с этой матрицей включаем в гамильтонов маршрут ребра (3,1) и (4,2).
В результате по дереву ветвлений гамильтонов цикл образуют ребра:
(1,4), (4,2), (2,3), (3,1). 
Длина маршрута равна = 29

 

5. Найти методом потенциалов оптимальный путь от пункта 1 к пункту 11.

 

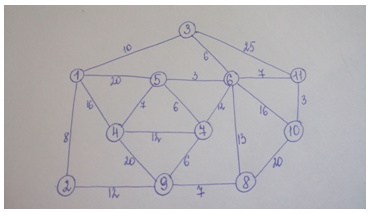
Решение:

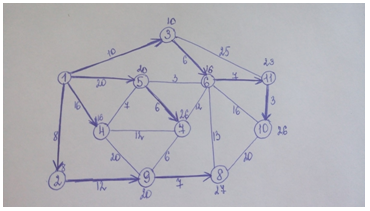
Считаем длину пути из пункта 1 в пункт 11: 10+6+7=23.

Ответ: 23.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---