Задачи онлайн по Теории вероятности и математической статистике

Тема: Задачи онлайн по Теории вероятности и математической статистике

Раздел: Бесплатные рефераты по теории вероятностей и математической статистике

Тип: Контрольная работа | Размер: 88.94K | Скачано: 268 | Добавлен 05.02.17 в 19:26 | Рейтинг: 0 | Еще Контрольные работы

2.5. В команде КВН 10(3+(К+M)(mod3))% студентов 1-го курса, 10( 1 +(К+M)(mod3))% - 2-го курса, а остальную часть команды в равных долях составляют студенты 3-го и 4-го курсов. Среди студентов i-го курса в команде 10((4+К+М - i)(mod6))% девушек (i = 1, 2, 3, 4). Какова вероятность того, что случайно выбранный член команды КВН - девушка?

Решение

В команде - 30% студентов 1 курса

10% студентов 2 курса

По 30% студентов 3 и 4 курсов

Среди студентов 1 курса девушек: 0%

2 курса: 50%

3 курса: 40%

4 курса: 30%

Обозначим через А – выбранный член команды КВН – девушка. Так как в команде нет девушек, учащихся на 1 курсе, то обозначим события В₁ – выбранная девушка из команды КВН учится на 2 курсе, В₂ – на 3 курсе, В₄ – на 4 курсе.

Р (В₁) = 0,1

Р (В₂)  = 0,3

Р (В₃) = 0,3

Условная вероятность того, что выбранная девушка учится на 2 курсе:

Р_В1(А) = 0,5

Р_В2(А) = 0,4

Р_В3(А) = 0,3

Вероятность того, что наудачу выбранный член команды КВН окажется девушкой, по формуле полной вероятности:

Р(А) = Р (В₁)* Р_В1(А) + Р (В₂)* Р_В2(А) + Р (В₃)* Р_В3(А) = 0,1*0,5 + 0,3*0,4 + +0,3*0,3 = 0,05+ 0,12 + 0,09 = 0,26

Ответ: Р(А) = 0,26

 

2.8. Имеется 25+(K+.M)(mod11) экзаменационных билетов, каждый из которых содержит два вопроса. Экзаменующийся знает ответ только на 2(19+(К+М)(mod11)) вопросов программы. Найти вероятность того, что экзамен будет сдан, если для этого достаточно ответить на оба вопроса своего билета или на один вопрос из своего билета и на один (по выбору преподавателя) вопрос из дополнительного билета.

Решение

Общее число вопросов в 34 билетах: 34*2 = 68 вопросов.

Пусть событие А – студент сдал экзамен, тогда событие А₁ – студент знал ответ на 1й вопрос, событие А₂ – студент знал ответ на 2-й вопрос. Так как успешная сдача экзамена предполагает ответы на оба вопроса, то:

Р(А) = Р(А₁) * Р(А₂)

Вероятность наступления события А1 = 56/68=14/17=0,82

Вероятность того, что студент знал ответ на 2й вопрос, при условии, что 1й вопрос был им подготовлен: А2 = 55/67

Тогда искомая вероятность сдачи экзамена:

Р(А) = Р(А1) * Р(А2) = 14/17*55/67 = 770/1139 = 0,676

Ответ: Р(А) =  0,676

 

2.13. Получена партия из 8+(К+М)(mod5)=12 изделий одного образца. По данным проверки 4+(К+М)(mod5)=8 изделий, три изделия оказались технически исправными, а остальные - бракованными. Определить вероятность того, что в партии 8-(К+М)(mod5)=4 исправных изделий, если в данной партии с одинаковой вероятностью возможно любое количество бракованных изделий.

Решение

Так как в результате проверки партии из 8 изделий, 3 оказались исправными, то необходимо вычислить вероятность, что из оставшихся 4 деталей, 1 окажется исправным. Так как вероятности одинаковы, то Р = ¼ = 0,25

Ответ: Р=0,25

 

2.19 В семизарядный пистолет с барабаном вставляется шесть патронов, часть из которых (возможно, все или ни одного) - холостые. Затем вставляется боевой патрон, после чего барабан случайно прокручивается и делается выстрел.

1. Какова вероятность того, что выстрел будет боевым, если все предположения о числе холостых патронов в барабане равновероятны?

2. Найти вероятность того, что в барабан первоначально было вставлено три холостых патрона, если известно, что выстрел оказался боевым.

Решение

1. Точно известно, что в барабане присутствует как минимум 1 боевой патрон: 1/7=0,14

Так как данные об оставшихся 6 патронах отсутствуют, то возможно любое число холостых и боевых патронов. Тогда можно сказать, что вероятность боевого выстрела будет не менее 14% и может достигать 100%. То есть вероятность заключена в интервал: [0,14;1]

2. Если в барабан первоначально было вставлено 3 холостых патрона, то в нем было 5 боевых патронов. Тогда вероятность того, что было вставлено 3 холостых патрона: 3/7 = 0,43

 

Индивидуальное задание № 2

3.4  3+(2К+М)(mod2) = 4 сигнализатора, которые работают независимо друг от друга. Вероятность отказа во время аварии i-го сигнализатора равна ((K+M)(mod3)+(i-l))/10, i=1,2,..., 3+(2K+M)(mod2). Рассматривается с.в. пси, - число сработавших во время аварии сигнализаторов.

Решение

Пусть p_i - вероятность срабатывания i-того сигнализатора во время аварии:

p₁ = 1 – 0 = 1

p₂ = 1 − 0.1 = 0.9

p₃ = 1 − 0.2 = 0.8

p₄ = 1 − 0.3 = 0.7

Пространство элементарных исходов Ω = { A_i | i = 1..16} , где

A₁ ={не сработали все четыре сигнализатора}

A₂ ={сработал только первый сигнализатор}

A₃ ={сработал только второй сигнализатор}

A₄ ={сработал только третий сигнализатор}

A₅ ={сработал только четвертый сигнализатор}

A₆ ={сработали только первый и второй сигнализаторы}

A₇ ={сработали только первый и третий сигнализаторы}

А₈ ={сработали только первый и четвертый сигнализаторы}

A₉ ={сработали только второй и третий сигнализаторы}

A₁₀ ={сработали только второй и четвертый сигнализаторы}

A₁₁ ={сработали только третий и четвертый сигнализаторы}

А₁₂ ={не сработал только 1й сигнализатор}

A₁₃ ={ не сработал только 2й сигнализатор}

A₁₄ ={ не сработал только 3й сигнализатор}

A₁₅ ={ не сработал только 4й сигнализатор }

A₁₆ ={сработали все четыре сигнализатора}      

P (A₁) = 0 ⋅ 0.1 ⋅ 0.2⋅ 0.3  = 0

P (A₂) = 1 ⋅ 0.1 ⋅ 0.2⋅ 0.3 = 0.006

P (A₃) = 0⋅ 0.9 ⋅ 0.2⋅ 0.3 = 0

P (A₄ ) = 0⋅ 0.1 ⋅ 0.8⋅ 0.3 = 0

P (A₅) = 0⋅ 0.1 ⋅ 0.2⋅ 0.7 = 0

P (A₆ ) = 1 ⋅ 0.9 ⋅ 0.2⋅ 0.3 = 0.054

P (A₇ ) = 1 ⋅ 0.1 ⋅ 0.8⋅ 0.3 = 0.024

P (A₈) = 1 ⋅ 0.1 ⋅ 0.2⋅ 0.7 = 0.014

P (A₉) = 0⋅ 0.9 ⋅ 0.8⋅ 0.3 = 0

P (A₁₀ ) = 0⋅ 0.9 ⋅ 0.2⋅ 0.7 = 0

P ( A₁₁) = 0⋅ 0.1 ⋅ 0.8⋅ 0.7 = 0

P (A₁₂) = 0 ⋅ 0.9 ⋅ 0.8⋅ 0.7 = 0

P (A₁₃) = 1⋅ 0.1 ⋅ 0.8⋅ 0.7 = 0.056

P (A₁₄ ) = 1⋅ 0.9 ⋅ 0.2⋅ 0.7 = 0.126

P ( A₁₅) = 0⋅ 0.9 ⋅ 0.8⋅ 0.3 = 0.216

P (A₁₆) = 1 ⋅ 0.9 ⋅ 0.8⋅ 0.7 = 0.504

Xi	0	1	2	3	4
Pi	P (A1) = 0	P (A2) + P (A3) + P (A4)+ P (A5)= =0.006+0+0+0 = 0.006	P (A6) + P (A7) + P (A8)+ P (A9) + P (A10)+ P (A11) =0.054+0.024+0.014+0 +0+0= 0.092	P (A12) + P (A13) + P (A14)+ P (A15)= 0+0.056+0.126+0.216 = 0.398	P (A16) = 0.504

 

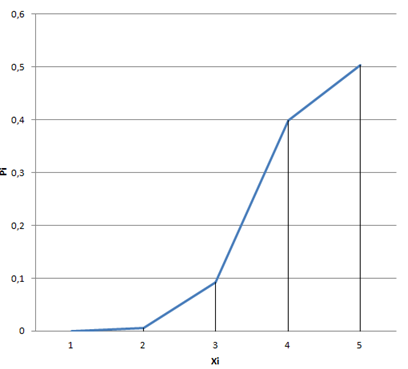
3.14 Из 5+(К+2М)(mod4)=5 сотрудников отдела некоторой коммерческой фирмы города N, среди которых три женщины и остальные мужчины, случайным образом формируется группа в составе 2+(К+2M)(mod4)=2 человек. Рассматривается с.в. ПСИ, - число мужчин в группе.

Решение

Рассмотрим события:

А=(в группу не войдет ни один мужчина)

В=(в группу войдет 1 мужчина)

С=(в группе будет 2 мужчин).

Общее число исходов: С_5^2=5!/2!(5-2)!=5!/2!3!=(4*5)/(1*2)=10

В группе 2 мужчины (событие С): 2 мужчин в группу из имеющихся 2 мужчин можно взять С_2^2 способами, тогда число благоприятствующих исходов равно: С_2^2 С_(5-2)^(2-2)

Тогда Р(С) = (С_2^2 С_(5-2)^(2-2))/(С_5^2 ) = (С_2^2 С_3^0)/(С_5^2 ) = 1/10 = 0,1

В группе 1 мужчина (событие В): 1 мужчину в группу из имеющихся 2 мужчин можно взять С_2^1 способами, тогда число благоприятствующих исходов равно: С_2^1 С_(5-2)^(2-1)

Тогда Р(В) = (С_2^1 С_(5-2)^(2-1))/(С_5^2 ) = (С_2^1 С_3^1)/(С_5^2 ) = (2*3)/10 = 0,6

В группе нет мужчина (событие С): из имеющихся 2 мужчин можно составить группу без мужчин можно С_2^0 способами, тогда число благоприятствующих исходов равно: С_2^0 С_(5-2)^(2-0)

Тогда Р(С) = (С_2^0 С_(5-2)^(2-0))/(С_5^2 ) = (С_2^0 С_3^2)/(С_5^2 ) = (1*3)/10 = 0,3

 

3.24
{█(р(х)= с(2-।х+1।),х ∈ (а,b)@p(x)=0,x∉(a,b))┤
Где а= -3+(К+М) (mod 2)= -2, b=1+(K+M) (mod2)= 2
{█(р(х)= с(2-।х+1।),х ∈ (-2,2)@p(x)=0,x∉(-2,2))┤
    Найдем неизвестную константу:
∫_(-∞)^∞▒〖p(x)dx=〗 ∫_(-∞)^∞▒〖с(2-।х+1।)dx=〗 ∫_(-2)^2▒〖с(2-।х+1।)dx=〗  (cx(2-।х+1।))/2 |_(-2)^2=  (c2(2-।2+1।))/2 – (c(-2)(2-।-2+1।))/2 = -c – c= -2c = 1
c=0,5
График плотности распределения на интервале (-2;2), на остальном промежутке плотность распределения равна 0.

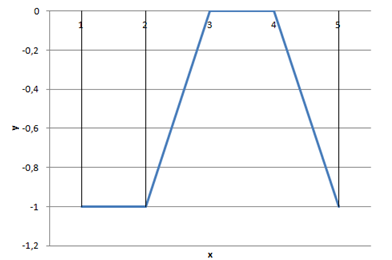
Найдем F(x) = ∫_ ^ ▒p(x)dx

F(x) = (x(2-।х+1।))/4

График функции:

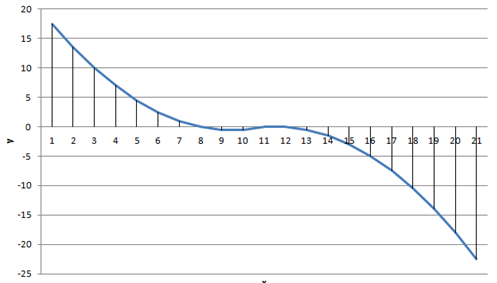
Мξ = ∫_(-∞)^∞▒〖x*p(x)dx=〗 ∫_(-∞)^∞▒〖x*((2-।х+1।)/2)dx=〗
= ∫_(-2)^2▒〖(2-।х+1।)x/2 dx=〗 〖((2-।х+1।) x^2*x)/4|〗_(-2)^2 = (2-।2+1।)8/4 - ((2-।-2+1।)(-8))/4 =
= -2 – (-2) = 0

Dξ = ∫_(-∞)^∞▒〖x^2*p(x)dx-〗 0 = ∫_(-2)^2▒〖x^2*(2-।х+1।)/2 dx〗 -0 =
= ((2-।х+1।) x^3*x)/6 |_(-2)^2-0  = – 0,167 –0,167 = -0,334
σξ = √Dξ=0,577

Определить вероятности

P{ ξ<0 } = P(∫_(-∞)^0▒〖p(x)dx)=〗  (2-।х+1।)/2=1/2

P{ξ≥ 0 + 0.9)}= = P(∫_0.9^∞▒〖p(x)dx)=〗  (2-।х+1।)/2=0,1

P{│ξ-0│≤ 0,577 }= P(∫_(-∞)^0,577▒〖p(x)dx)=〗  (2-।х+1।)/2=0,125

 

3.29

Решение

f(x) = {█(0,x≤-9@|x|,-99)┤

F(x) = ∫_ ^ ▒f(x)dx

F(x) = {█(0,x≤-9@x|x|@0,x>9)┤,-9

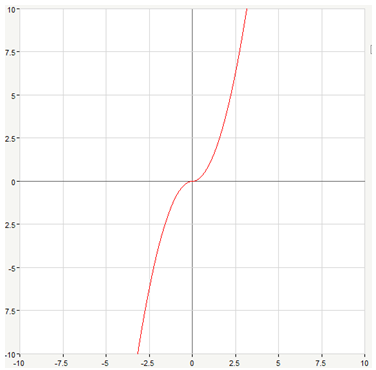
Мξ = ∫_(-∞)^∞▒〖x*f(x)dx=〗 ∫_(-9)^9▒〖x*|x|dx=〗 x^2 |x||_(-9)^9 = 0

Dξ = ∫_(-∞)^∞▒〖x^2*f(x)dx-〗 М^2 ξ = ∫_(-9)^9▒〖x^2*|xdx-〗 0 = x^3 |x||_(-9)^9-0= 6561+6561 = 13122

σξ = √Dξ=114,55

Определить вероятности

P{ ξ<0 } = P(∫_(-∞)^0▒〖p(x)dx)=〗|x|=1/2

P{ξ≥ 0 + 0.9)}= = P(∫_0.9^∞▒〖p(x)dx)=〗|x|=0,4

P{│ξ-0│≤ 114,55 }= P(∫_(-∞)^114,55▒〖p(x)dx)=〗|x|=0,85

 

3.34

F(x) = {█(0,x≤5@(x-7)/20,57))┤

f(x) =F’(x)

Значит:

f(x) = {█(0,x≤5@-7/20,57))┤

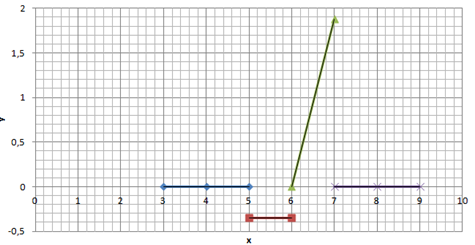
(перерисовывать одинаковым цветом)

Мξ = ∫_(-∞)^∞▒〖x*f(x)dx=〗 ∫_6^7▒〖x*1,88(x-6)dx〗 = 1,88(2x-6)|_6^7=15,04 – 11,26 = 3,78

Dξ = ∫_(-∞)^∞▒〖x^2*f(x)dx-〗 М^2 ξ = ∫_6^7▒〖x^2*1,88(x-6)dx〗-14,3 =1,88(3x2 – 12x) |_6^7 –
 -14,3= 118,44 – 67,68-14,3 = 36,43

σξ = √Dξ=6,04

Определить вероятности

P{ ξ<3,78 } = 0,4

P{ξ≥ 3,78 + 0.9)}=0,3

P{│ξ+1│≤ 6,04 }=0,6

 

3.39 Расход бензина автобусом определенной модели (на 100 км пути) является с.в., подчиняющейся нормальному распределению со средним значением 15+(K+M)(mod5) =19 кг и стандартным отклонением 2+(K+M)(mod5)=6 кг. На некоторой автобазе города N составлена Инструкция, согласно которой автобус отправляется в профилактический ремонт, если при испытании он расходует более 17+(3K+M)(mod5)=18 кг бензина на 100 км пути.

Найти вероятность отправки в профилактический ремонт исправного автобуса. Как необходимо составить Инструкцию, чтобы эта вероятность была не более (2+(K+M)(mod9))/100=0,02?

Решение

Так как расход бензина подчиняется нормальному распределению, то закон можно записать как:

f(x) = 1/(6√2π) e^(-(x-19)^2/(2*6^2 )) = 1/15 e^(-(x-19)^2/72)    

Вероятность попадания величины расхода бензина в интервал [18;19]

P(18,19) = ∫_18^19▒f(x)dx=∫_18^19▒〖1/15 e^(-(x-19)^2/72) dx〗 = (-1*72)/(15*2(x-19)) e^(-(x-19)^2/72) |_18^19 = (-72)/(30(18-19)) e^(-(18-19)^2/72) –

(-1*72)/(15*2(19-19)) e^(-(19-19)^2/72) = 0,24*0,987 - 0 = 0,237

Так как значение функции при х=19 всегда равно 0, то найдем необходимое значение расхода для Инструкции:

(-1*72)/(15*2(x-19)) e^(-(x-19)^2/72)= 0,02    

(-2,4)/((x-19)) e^(-(x-19)^2/72)= 0,02

1/((x-19)) e^(-(x-19)^2/72)= - 0,008

Решив уравнение, получим х=23

Ответ: чтобы вероятность была не более 0,02, необходимо, чтобы профилактический ремонт наступал при расходе в 23 кг.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---