Контрольная №2 по Линейной алгебре Вариант №48

Тема: Контрольная №2 по Линейной алгебре Вариант №48

Раздел: Бесплатные рефераты по линейной алгебре

Тип: Контрольная работа | Размер: 241.15K | Скачано: 220 | Добавлен 30.01.17 в 15:29 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Институт права и экономики

Год и город: Липецк 2016

СОДЕРЖАНИЕ

Задание 1 …………………………………………………………………….…...	3
Задание 2 ……………………………………………...…………………..……...	5
Задание 3 …………………………………………………………………....……	7
Задание 4 ………………………………………………………...…….…………	9
Задание 5 ……………………………………………………...…………….……	12
Список использованной литературы ………………………………...…………	14

 

ЗАДАНИЕ 1

Дано комплексное число z₁. Записать число в алгебраической и тригонометрической формах и изобразить на комплексной плоскости. Найти все корни уравнения z×m + z₁ = 0 и изобразить их на комплексной плоскости.

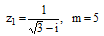
Решение:

Запишем число в алгебраической форме:

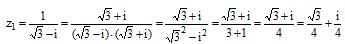
Найдём модуль комплексного числа:

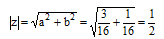
Найдём аргумент комплексного числа:

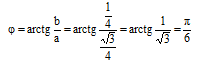
Тогда тригонометрическая форма имеет вид:

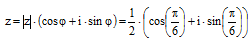
Решим корень уравнения:

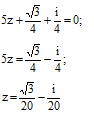
Изобразим на комплексной плоскости:

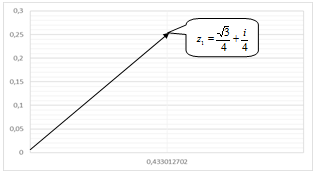
Рисунок 1. - Изображение комплексного числа вектором

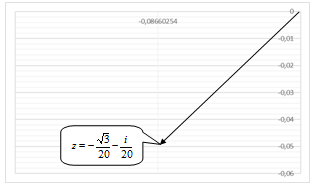
Рисунок 2. - Корень уравнения комплексного числа

Ответ:

 

ЗАДАНИЕ 2

Найти множество точек на плоскости комплексного числа z, которые определяются заданными условиями

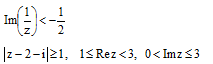
Решение:

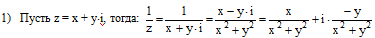
Находим:

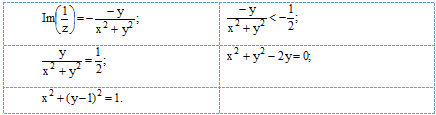
Получаем множество точек внутри окружности с центром в точке (0; 1) радиуса r = 1 (заштрихованная область):

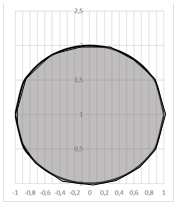
Рисунок 3. - Множество точек внутри окружности

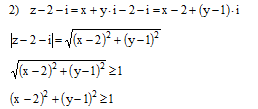
Получаем множество точек вне окружности с центром в точке (2; 1) радиуса r = 1.

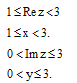
Получим множество точек (заштрихованная область):

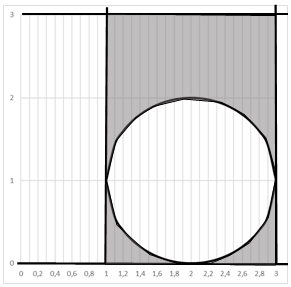
Рисунок 4. - Множество точек вне окружности

 

ЗАДАНИЕ 3

Выполнить следующие операции с векторами:

Заданы векторы: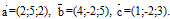

Найти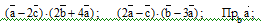 

направляющие косинусы вектора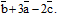 

Решение:

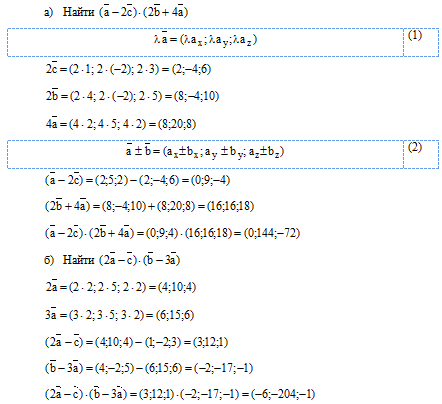
г)       Найти направляющие косинусы вектора 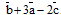  координаты векторов 

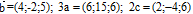
Найдём сумму координат вектора и модуль вектора

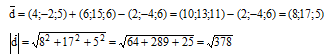
Направляющие косинусы определяются по формулам:

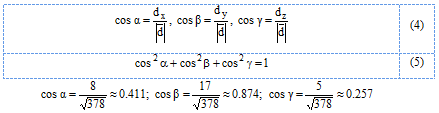
Выполним проверку:

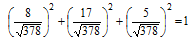
Проверка показывает, что задание выполнено правильно.

 

ЗАДАНИЕ 4

Дан треугольник с вершинами в точках А, В, С. Требуется:

а)   написать уравнения сторон (АВ), (АС), высоты (СН), медианы (СМ). Построить эти прямые;

б)   найти длину высоты СН;

в)   найти косинус угла между прямыми (СН) и (СМ).

А (-3; 4), В (7; 4), С (5; -2).

Решение:

а)   Уравнение прямой, проходящей через две точки:

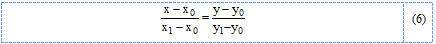
Уравнение стороны АВ:

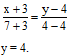
Уравнение стороны АС:

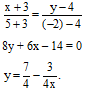
Так как прямые АВ и СН перпендикулярны, а прямая АВ параллельна оси Ох, то прямая СН параллельна оси Оу. Подставляя координаты точки С, получим уравнение СН:

х = 5.

Найдём координаты точки М – середины стороны АВ:

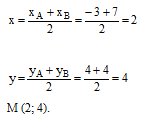
Уравнение медианы СМ (уравнение прямой, проходящей через точки С и М):

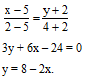
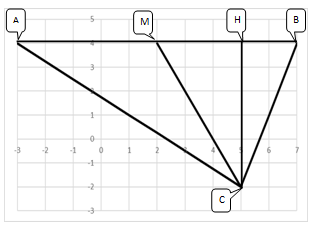
Рисунок 5. - Прямые (АВ), (АС), (СН), (СМ)

б)   Найдём координаты точки Н (точки пересечения прямых АВ у = 4 и СН х = 5):

Н (5; 4).

Длину высоты СН найдём как расстояние между двумя точками С и Н по формуле:

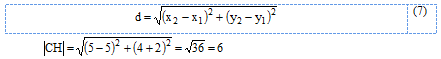
в)   Найдём длину медианы СМ:

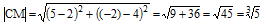
Косинус угла между прямыми СН и СМ равен (из прямоугольного треугольника СНМ):

 

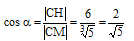
ЗАДАНИЕ 5

Найти объём пирамиды ABCD, если:

А = (-2; 3; -1), В = (2; 4; -1), С = (-3; 7; 2), D = (-2; 4; 1)

Решение:

Тетраэдр - пирамида, у которой все грани равносторонние треугольники.

Пусть нам даны координаты вершин тетраэдра A;B;C;D, то последовательность действий для нахождения её объёма следующая:

а)   находим координаты векторов;

б)   находим 1/6 смешанного произведения векторов  .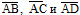

а)   Найдём векторы трёх рёбер тетраэдра, например, из вершины А. Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим:

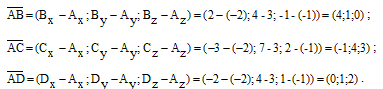
б)   Найдём смешанное произведение заданных векторов. Для этого составим определитель, по строкам которого записаны координаты векторов 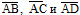 и вычислим его по правилу треугольника:

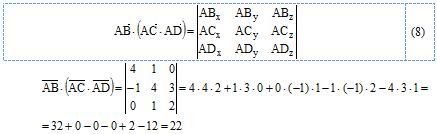
Объём пирамиды (тетраэдра), построенной на векторах 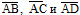 , равен одной шестой модуля смешанного произведения этих векторов:

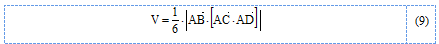
Тогда искомый объём:

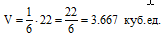
Ответ: Объём пирамиды 3.667 кубических единиц.

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Кремер, Н.Ш. Высшая математика для экономистов [Текст]: учебник для вузов – М.: ЮНИТИ, 2004. – 471 с.
2. Кремер, Н.Ш. Практикум по высшей математике для экономистов [Текст]: учебник для вузов – М.: ЮНИТИ-ДАНА, 2005. – 423 с.
3. Письменный, Д. Т. Конспект лекций по высшей математике [Текст]: полный курс / Письменный Д. Т. - М.: Айрис-пресс, 2006. - 608 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах [Текст]: учебное пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: ООО «Издательский дом «ОНИКС 21 век»», 2005. – Ч. I. – 304 с.
5. Лунгу, К.Н. Сборник задач по высшей математике. 1 курс [Текст]: К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. – М.: Айрис–пресс, 2004. – 576 с.
6. Солодовников, А.С. Математика в экономике [Текст]: учебник для студентов / Солодовников А.С., Бабайцев В.А., Браилов А.В. - М.: Финансы и статистика, 2000. - Ч.1 - 224с.
7. Красс, М.С. Математика для экономистов [Текст]: учебное пособие / Красс М.С., Чупрынов Б.П. – СПб.: Питер, 2005. – 464 с.
8. Черненко, В.Д. Высшая математика в примерах и задачах [Текст]: учебное пособие для вузов / в 3т.: том 1 - СПб.: Политехника, 2003. – 703 с.
9. Плис, А.И. Mathcad: Математический практикум для экономистов и инженеров [Текст]: учебное пособие / Плис А.И., Сливина Н.А. - Издательство: Финансы и статистика, 2003. - 656 с.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---