Контрольная №1 по Линейной алгебре Вариант №48

Тема: Контрольная №1 по Линейной алгебре Вариант №48

Раздел: Бесплатные рефераты по линейной алгебре

Тип: Контрольная работа | Размер: 156.50K | Скачано: 241 | Добавлен 30.01.17 в 15:23 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Институт права и экономики

Год и город: Липецк 2016

ЗАДАНИЕ 1

Вычислить определитель

Решение:

Найдём определитель матрицы, для этого приведём матрицу к треугольному виду, т.е. к такому виду, при котором все элементы ниже диагонали равны 0. При таком виде определитель равен произведению элементов по диагонали.

Вычтем первую строку из остальных строк так, что бы в первом столбце все элементы ниже обратились в 0, помножая на 0.4; -0.6; 1.4

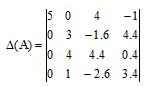
вычтем вторую строку из остальных строк так, что бы в втором столбце все элементы ниже обратились в 0, помножая на 1.333; 0.333

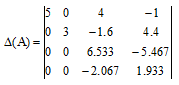
вычтем третью строку из остальных строк так, что бы в третьем столбце все элементы ниже обратились в 0, помножая на -0.316

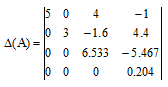
Определитель матрицы равен произведению элементов по главной диагонали:

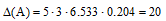
Ответ: D(А) = 20

 

ЗАДАНИЕ 2

С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.

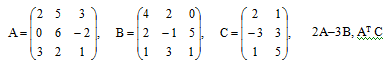
Решение:

Построим обратную матрицу. Для этого совершим ряд действий.

Найдём определитель матрицы, применяя правило треугольников

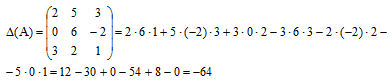
Определитель матрицы D(А) = -64 ¹ 0, т.е. матрица А – невырожденная и обратная матрица А^-1 существует.

Найдём алгебраические дополнения А_ij элементов матрицы и составляем из них присоединённую матрицу А.

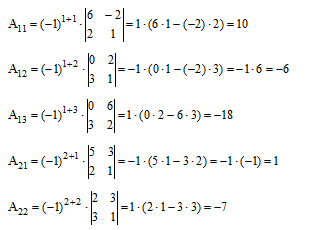
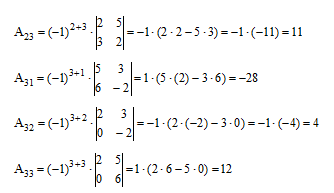
Составляем матрицу А из алгебраических дополнений и транспонируем её А.

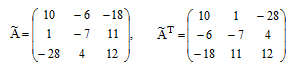
Используя формулу обратной матрицы, найдём её

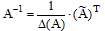
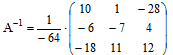
Проверим истинность результата одного из равенств

А × А-1 = А-1 ×А = Е

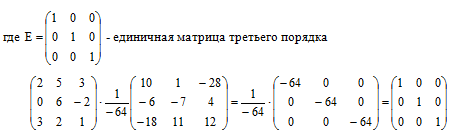
Элементы матрицы-результата совпадают с элементами единичной матрицы Е. Следовательно, проверка пройдена успешно, обратная матрица А^-1 найдена верно.

С матрицами А, В, С совершим действия:

Произведением матрицы на число

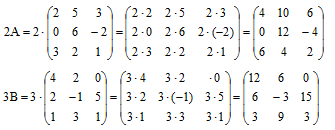
Разностью двух матриц

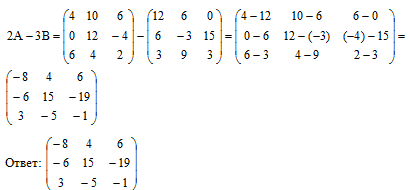
Произведением двух матриц

 

 

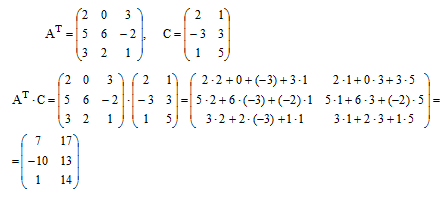
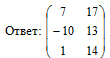
ЗАДАНИЕ 3

Найти ранг матрицы

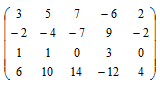
Решение:

Для вычисления ранга приведём матрицу к ступенчатому виду, используя элементарные преобразования над строками и столбцами матрицы, (метод Гаусса).

Матрица называется ступенчатой, если в каждой её строке первый ненулевой элемент стоит правее, чем в предыдущей (т.е. получаются ступеньки, высота каждой ступеньки должна быть равна единице).

Первую строку делим на 3

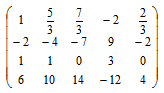
к второй строке добавляем первую строку, умноженную на 2;

от третьей строки отнимаем первую строку, умноженную на 1;

от четвёртой строки отнимаем первую строку, умноженную на 6

Получили ступенчатую матрицу. Ранг полученной матрицы равен двум (r=2), так как после вычёркивания последних двух строк, полностью состоящей из нулей, в ней останется две ненулевые строки.

Ответ: r(A) = 2

 

ЗАДАНИЕ 4

Решить системы линейных уравнений: а) методом Крамера; б) с помощью обратной матрицы

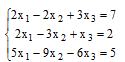
Решение:

а) методом Крамера

Вычисляем определитель матрицы системы, разлагая его по первой строке

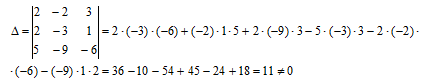
Так как определитель не равен нулю, то система уравнений имеет единственное решение.

Вычислим определители D₁, D₂, D₃ из определителя D заменой первого, второго и третьего столбцов столбцом свободных членов

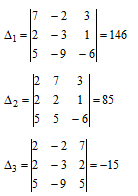
Теперь воспользуемся формулой Крамера и найдём все переменные

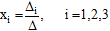
где D_i – определитель матрицы, получаемой из матрицы системы заменой i – ого столбца столбцом свободных членов.

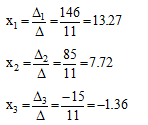
Ответ: х₁ = 13.27, х₂ = 7,72, х₃ = -1.36

б) с помощью обратной матрицы

Данная система уравнений может быть записана матричным уравнением

А × Х = В

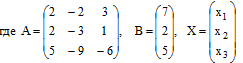
Решение уравнения найдём по формулам

А-1 ×АХ = А-1 ×В

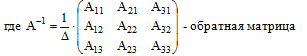
Выразив из этого уравнения Х, получим

Х = А^-1×В

Определитель матрицы

Так как D(А) ¹ 0, то система имеет единственное решение, которое можно найти методом обратной матрицы. Найдём обратную матрицу А^-1 с помощью присоединённой матрицы. Вычислим алгебраические дополнения A_ij к соответствующим элементам матрицы А

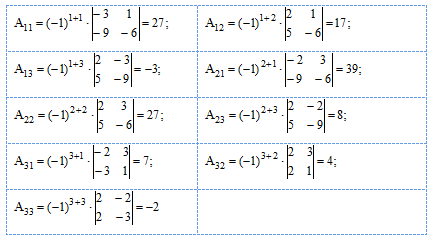
Составляем матрицу А из алгебраических дополнений и транспонируем её А

Используя формулу (1) найдём обратную матрицу

 

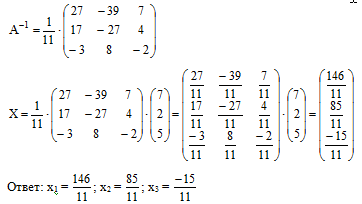
ЗАДАНИЕ 5

Решить системы линейных уравнений методом Гаусса

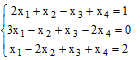
Решение:

Процесс решения системы уравнений методом Гаусса состоит из двух этапов. На первом этапе система приводится к ступенчатому виду, путём последовательного исключения переменных. На каждом шаге решения справа располагается расширенная матрица, эквивалентная системе уравнений. Исключим переменную x₁ из всех уравнений, за исключением первого.

Поменяем местами уравнения 1 и 3.

Из уравнения 2 вычитаем уравнение 1, умноженное на 3

Из уравнения 3 вычитаем уравнение 1, умноженное на 2

Исключим переменную x₂ из последнего уравнения.

Из уравнения 3 вычитаем уравнение 2.

Данная система приведена к ступенчатому виду. Последовательно найдём значения переменных. Начнём с последнего уравнения.

Рассмотрим уравнение 3 последней получившейся системы, из данного уравнения найдём значение переменной x₃

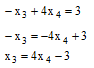
Рассмотрим уравнение 2 последней получившейся системы, из данного уравнения найдём значение переменной x₂ и подставим, ранее найденное, значение переменной x₃

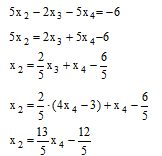
Рассмотрим уравнение 1 последней получившейся системы, из данного уравнения найдём значение переменной x₁ и подставим, ранее найденные, значения переменных x₂ , x₃

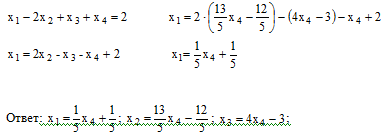
х₄ - свободная переменная. Система имеет бесконечное множество решений.

 

ЗАДАНИЕ 6

В таблице приведены данные об исполнении баланса за отчётный период в условных денежных единицах. Вычислить необходимый объём валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличится в k =2.5 раз, а второй отрасли на m =80 %

Таблица 1 – Исходные данные

Отрасль		Потребление		Конечный продукт	Валовый выпуск
		1	2
Производство	1	20	40	60	120
	2	10	5	25	40

Решение:

Рассчитаем новый конечный продукт Y:

Y₁ = 60 · 2.5 = 150

Y₂ = 25 + 80% = 45

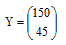
Тогда необходимый объём валового выпуска Х каждой отрасли

высчитывается по формуле:

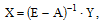
где А – матрица коэффициентов прямых затрат:

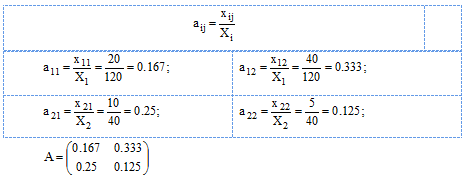
Рассчитаем матрицу К = (Е – А):

Вычислим матрицу полных затрат:

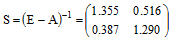
Тогда объём валового выпуска:

Ответ: необходимый объём валового выпуска каждой отрасли составит: Х₁ = 226.5; Х₂ = 116.1.

 

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Кремер, Н.Ш. Высшая математика для экономистов [Текст]: учебник для вузов – М.: ЮНИТИ, 2004. – 471 с.
2. Кремер, Н.Ш. Практикум по высшей математике для экономистов [Текст]: учебник для вузов – М.: ЮНИТИ-ДАНА, 2005. – 423 с.
3. Письменный, Д. Т. Конспект лекций по высшей математике [Текст]: полный курс / Письменный Д. Т. - М.: Айрис-пресс, 2006. - 608 с.
4. Данко, П.Е. Высшая математика в упражнениях и задачах [Текст]: учебное пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: ООО «Издательский дом «ОНИКС 21 век»», 2005. – Ч. I. – 304 с.
5. Лунгу, К.Н. Сборник задач по высшей математике. 1 курс [Текст]: К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. – М.: Айрис–пресс, 2004. – 576 с.
6. Солодовников, А.С. Математика в экономике [Текст]: учебник для студентов / Солодовников А.С., Бабайцев В.А., Браилов А.В. - М.: Финансы и статистика, 2000. - Ч.1 - 224с.
7. Красс, М.С. Математика для экономистов [Текст]: учебное пособие / Красс М.С., Чупрынов Б.П. – СПб.: Питер, 2005. – 464 с.
8. Плис, А.И. Mathcad: Математический практикум для экономистов и инженеров [Текст]: учебное пособие / Плис А.И., Сливина Н.А. - Издательство: Финансы и статистика, 2003. - 656 с.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---