Контрольная №2 по высшей математике (2 семестр)

Тема: Контрольная №2 по высшей математике (2 семестр)

Раздел: Бесплатные рефераты по высшей математике

Тип: Контрольная работа | Размер: 35.98K | Скачано: 344 | Добавлен 29.05.16 в 23:22 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Уральский экономический университет

Контрольная работа 2 (2 семестр)

Тема 9. Неопределенный интеграл

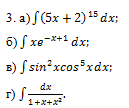
Решение:

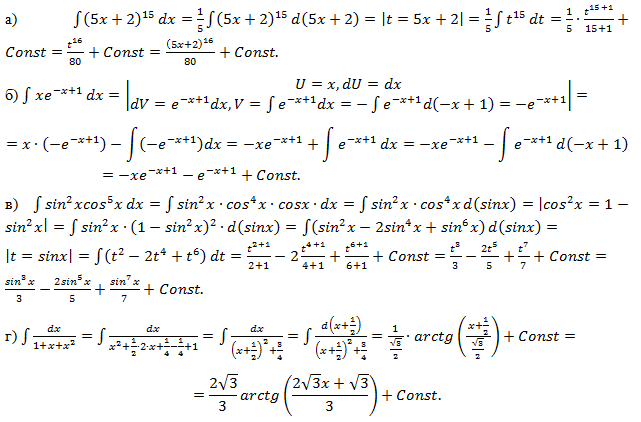
Ответ:

 

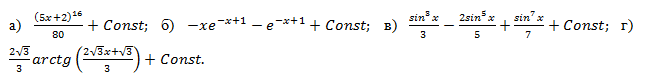
Тема 10. Определенный интеграл.

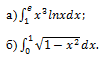
Решение:

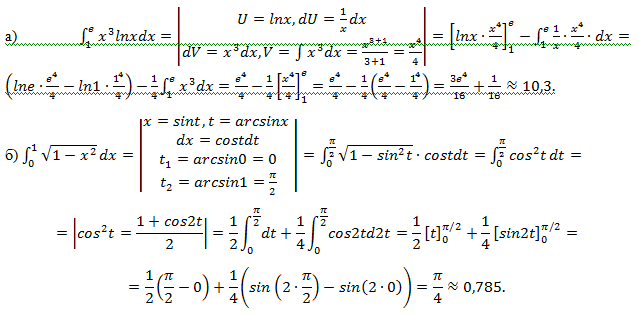
Ответ: а) (3e^4)/16+1/16≈10,3; б) π/4≈0,785.

 

10.2. Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж.

3. 4x^2-3y=0,2x-y=0.

Решение:

Построим фигуру:

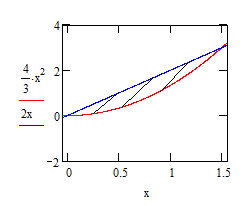
Найдем абсциссы точек пересечения кривой и прямой:

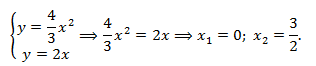
Общая площадь фигуры состоит из двух частей:

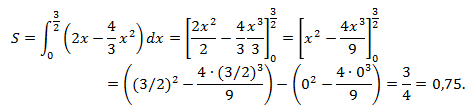
Ответ: S=3/4=0,75.

 

Тема 11. Несобственный интеграл

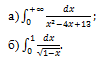
Решение:

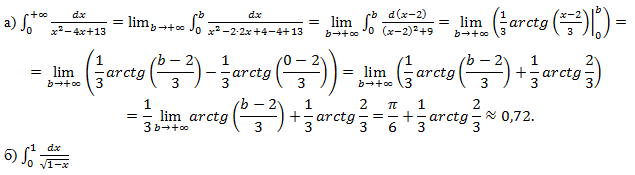
Подынтегральная функция стремится к бесконечности при x→1 поэтому действуем по определению несобственного интеграла

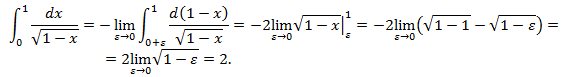
Ответ: а) π/6+1/3 arctg 2/3≈0,72; б) 2.,

 

Тема 12. Ряды

12.1. Числовые ряды. Исследовать ряд на сходимость.

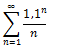
Решение:

Применим признак Даламбера

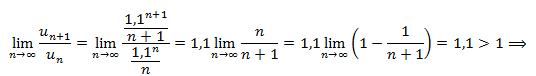
ряд расходится.

Ответ: ряд расходится.

 

Тема 13. Функции нескольких переменных

Исследовать функцию на экстремум.

z=y^3+yx^2+x.

Решение:

1. Функция определена для всех значений переменных x,y
2. Находим частные производные первого порядка и составляем систему для определения координат точек, в которых возможен экстремум

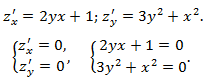
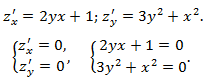
Данная система не имеет стационарных точек, следовательно, экстремумов нет.

Ответ: экстремумов нет.

 

Тема 15. Решение дифференциальных уравнений

3. y^'+2y/x=x^3,y(1)=1.

Решение:

Решаем уравнение методом Бернулли.

1. Решение уравнения ищем в виде произведения двух функций

y=U(x)∙V(x),y^'=U^'∙V+U∙V^'.

2. Подставляем выражение для функции и ее производной в уравнение, группируем слагаемые и выносим общий множитель

U^' V+UV^'+2UV/x=x^3

U^' V+U(V^'+2V/x)=x^3

3. Приравниваем выражение в скобках к нулю, получаем систему двух дифференциальных уравнений для нахождения функций U(x) и V(x)

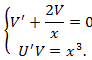
4. Из 1-го уравнения находим функцию V(x)

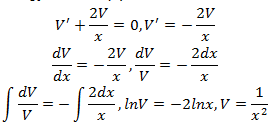
5. Полученное выражение для функции V подставляем во 2-е уравнение системы

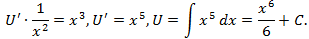
6. Записываем общее решение

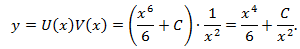
7. Подставляем начальное условие y(1)=1

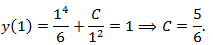
Тогда частное решение есть

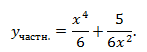
Ответ: 

 

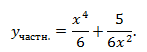
15.2. Найти общее решение дифференциального уравнения

y^''-4y^'+4y=3x-3x^2

Решение:

• характеристическое уравнение

Составим характеристическое уравнение соответствующего однородного уравнения

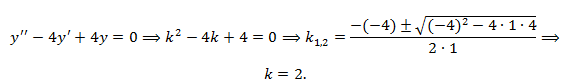
Итак, корни характеристического уравнения равны, следовательно, общее решение однородного уравнения:

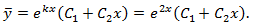
Решение исходного неоднородного уравнения y^''-4y^'+4y=3x-3x^2  найдем методом неопределенных коэффициентов. f(x)=3x-3x^2– многочлен 2-ой степени.

y^*=Ax^2+Bx+C

Найдем коэффициенты A,B,C:

y^(*')=2Ax+B; y^(*'')=2A;

2A-4(2Ax+B)+4(Ax^2+Bx+C)=3x-3x^2⟹

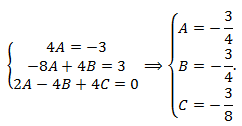
Общее решение:

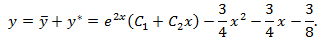
Ответ: y=e^2x (C_1+C_2 x)-3/4 x^2-3/4 x-3/8.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---