Контрольная работа по Статистике (вариант не указан)

Тема: Контрольная работа по Статистике (вариант не указан)

Раздел: Бесплатные рефераты по статистике

Тип: Контрольная работа | Размер: 28.59K | Скачано: 283 | Добавлен 06.04.16 в 03:12 | Рейтинг: 0 | Еще Контрольные работы

Содержание

Задача 1. 3

Задача 2. 4

Задача 3. 7

Задача 4. 9

Задача 5. 10

Список использованной литературы.. 12

 

Задача 1

Построить полигон по следующему вариационному ряду:

х	1	3	4	8
mx	20	10	14	6

Найти ряд накопленных частот и построить кумулятивную кривую.

Решение

Полигон частот  - это ломанная, отрезки которой соединяют точки (x₁; m₁), (x₂; m₂), ..., (x_k; m_k). Для проведения построения полигона частот на оси абсцисс откладываем варианты x_i, а на оси ординат - соответствующие им частоты m_i. Точки ( x_i; m_i) соединяем отрезками прямых  и  получаем полигон  частот (рис. 1).

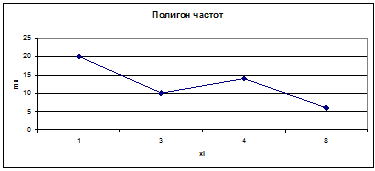
Рис. 1. Полигон частот

Накопленные частоты определяются путем последовательного прибавления к частотам (или частостям) первой группы этих показателей последующих групп ряда распределения. 

Определим ряд накопленных частот:

x	mx	Накопленная частота, S
1	20	20
3	10	30
4	14	44
8	6	50
Итого	50

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты.

Построим кумулятивную кривую (рис. 2).

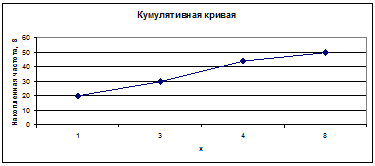
Рис. 2. Кумулятивная кривая

 

Задача 2

Построить гистограмму и полигон по следующему вариационному ряду.

Интервал	0–1,5	1,5–3	3–4,5	4,5–6
Относительная частота	0,3	0,2	0,4	?

Найти ряд накопленных относительных частот и построить кумулятивную кривую.

Решение

Определим неизвестную относительную частоту исходя из условия, что сумма относительных частот равна единице, тогда:

При построении гистограммы относительных частот на оси абсцисс откладываются интервалы, а относительные частоты изображаются прямоугольниками, построенными на соответствующих интервалах.

Построим гистограмму по заданному вариационному ряду (рис. 1):

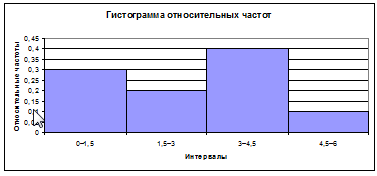
Рис. 1. Гистограмма относительных частот

Накопленные частоты определяются путем последовательного прибавления к частотам (или частостям) первой группы этих показателей последующих групп ряда распределения. 

Определим ряд накопленных относительных частот:

Интервал	Середина интервала, xi	Относительная частота	Накопленная относительная частота, w
0–1,5	0,75	0,3	0,3
1,5–3	2,25	0,2	0,5
3–4,5	3,75	0,4	0,9
4,5–6	5,25	0,1	1
Итого		1

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным относительным частотам. При этом на оси абсцисс помещают значения середины интервала, а на оси ординат — накопленные относительные частоты.

Построим кумулятивную кривую (рис. 2).

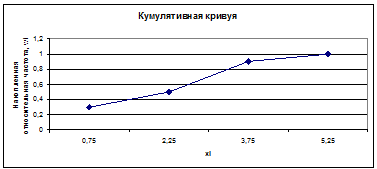
Рис. 2. Кумулятивная кривая

 

Задача 3

Вычислить моду, медиану, среднюю арифметическую, дисперсию, коэффициент асимметрии и эксцесс для следующего вариационного ряда.

x	12	14	16	18	20	22
wx	0,05	0,15	0,5	0,16	0,1	0,04

Решение

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

Максимальное значение повторений при x = 16 (w_x=0,5). Следовательно, мода равна 16.

Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим x_i, при котором накопленная относительная частота будет больше ∑w_x/2 = 0,5. Это значение x_i = 16. Таким образом, медиана равна  16.

Математическое ожидание находим по формуле:

M[x] = ∑x_iw_i.

Математическое ожидание M[X]:

M[x] = 12*0.05 + 14*0.15 + 16*0.5 + 18*0.16 + 20*0.1 +

+ 22*0.04  = 16.46.

Дисперсию находим по формуле:

D[X] = ∑x²_iw_i - M[x]².

Дисперсия D[X]:

D[X] = 12²*0.05 + 14²*0.15 + 16²*0.5 + 18²*0.16 +

+ 20²*0.1 + 22²*0.04  - 16.46² = 4.868.

Среднее квадратическое отклонение σ(x):

Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии:

As = M₃/σ³

где M₃ - центральный момент третьего порядка.

xi	wi	M3 = (x-M[x])3wi	M4 = (x-M[x])4wi
12	0.05	-4.436	19.785
14	0.15	-2.233	5.493
16	0.5	-0.0487	0.0224
18	0.16	0.584	0.899
20	0.1	4.436	15.703
22	0.04	6.801	37.678
Итого		5.103	79.58

As = 5.103/10.742 = 0.49.

Положительная величина указывает на наличие правосторонней асимметрии.

Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

Чаще всего эксцесс оценивается с помощью показателя:

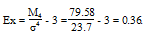
где M₄ - центральный момент четвертого порядка.

Ответ:

 

Задача 4

Найти среднюю арифметическую и среднее квадратическое отклонение для ряда распределения.

Интервал	6,67–6,69	6,69–6,71	6,71–6,73	6,73–6,75
Частота	5	17	24	54
Интервал	6,75–6,77	6,77–6,79	6,79–6,81	6,81–6,83
Частота	52	23	18	7

Решение

Составим таблицу для расчета показателей:

Интервал	Середина интервала, xi	Частота, fi	xi * fi	Накопленная частота, S	(x - xср)2*f
6.67 - 6.69	6.68	5	33.4	5	0.025
6.69 - 6.71	6.7	17	113.9	22	0.0437
6.71 - 6.73	6.72	24	161.28	46	0.0226
6.73 - 6.75	6.74	54	363.96	100	0.00618
6.75 - 6.77	6.76	52	351.52	152	0.0045
6.77 - 6.79	6.78	23	155.94	175	0.0197
6.79 - 6.81	6.8	18	122.4	193	0.0437
6.81 - 6.83	6.82	7	47.74	200	0.0336
Итого		200	1350.14		0.2

 Для оценки ряда распределения найдем следующие показатели.

Средняя взвешенная (выборочная средняя):

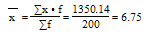
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего):

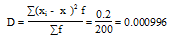
Среднее квадратическое отклонение (средняя ошибка выборки):

Каждое значение ряда отличается от среднего значения 6.75 в среднем на 0.0316.

Ответ:

 

Задача 5

Рассчитать среднее количество сотрудников на предприятиях связи города, используя данные, приведенные в таблице.

Численность работников, чел.	3	4	5	6	Всего
Количество отделений	26	65	42	17	150

Решение

Для расчетов введем обозначения:

х_i – численность работников, чел.;

f_i – количество отделений.

Для определения среднего количества сотрудников на предприятиях связи города используем формулу средней взвешенной (выборочной средней):

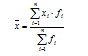
Подставляем в формулу значения, приведенные в таблице:

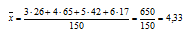
Ответ: среднее количество сотрудников на предприятиях связи города равно 4,33.

 

Список использованной литературы

1. Балдин, К.В. Общая теория статистики: Учебное пособие / К.В. Балдин, А.В. Рукосуев. - М.: Дашков и К, 2012. - 312 c.
2. Батракова, Л.Г. Теория статистики: Учебное пособие / Л.Г.Батракова. - М.: КноРус, 2013. - 528 c.
3. Громыко, Г.Л. Теория статистики: Практикум / Г.Л. Громыко. - М.: НИЦ ИНФРА-М, 2013. - 238 c.
4. Елисеева И.И. Общая теория статистики: учебник для вузов / И.И. Елисеева, М.М. Юзбашев; под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2009. – 656 с.
5. Ефимова М.Р. Практикум по общей теории статистики: учебное пособие для вузов / М.Р. Ефимова и др. – М.: Финансы и статистика, 2007. – 368 с.
6. Лысенко, С.Н. Общая теория статистики: Учебное пособие / С.Н. Лысенко, И.А. Дмитриева. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2013. - 208 c.
7. Маличенко, И.П. Общая теория статистики: Курс лекций с практическими примерами / И.П. Маличенко, О.Е. Лугинин. - Рн/Д: Феникс, 2010. - 187 c.
8. Шмойлова Р.А. Практикум по теории статистики: учебное пособие для вузов / Р.А. Шмойлова и др.; под ред. Р.А. Шмойловой. - М.: Финансы и статистика, 2007. – 416 с.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---