Контрольная по Анализу данных в Excel Вариант 4

Тема: Контрольная по Анализу данных в Excel Вариант 4

Раздел: Бесплатные рефераты по анализу данных

Тип: Контрольная работа | Размер: 505.74K | Скачано: 319 | Добавлен 06.03.16 в 16:25 | Рейтинг: 0 | Еще Контрольные работы

Вуз: Финансовый университет

Год и город: Краснодар 2015

Контрольная работа №1
Вариант № 4

План контрольной работы.

1. Посчитайте выборочное среднее.

2. Выборочная дисперсия. Стандартное отклонение.

Посчитайте стандартное отклонение и дисперсию для предыдущего примера.

3. Сгенерируйте распределенную по закону Пуассона случайную величину.

Постройте гистограмму, иллюстрирующую плотность распределения.

4. Коэффициент корреляции и его значения.

5. Посчитайте их к-т корреляции, сделайте вывод о степени их коррелированности.

6. Регрессионный анализ.

7. Проведите регрессионный анализ.

8. Проведите двухфакторный регрессионный анализ взяв зависимой переменной Y.

9. Расскажите цель применения дисперсионного анализа.

 

1. Дана выборка значений случайной величины.
X	2,1	3,5	2,8	2,7	3,2
Посчитайте выборочное среднее.

Ответ:

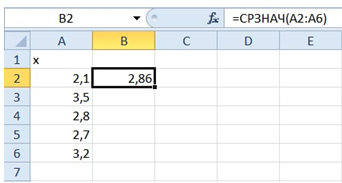
2. Что такое выборочная дисперсия? Как считается стандартное отклонение?

Посчитайте стандартное отклонение и дисперсию для предыдущего примера.

Ответ:

Выборочная дисперсия в математической статистике — это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки.

Стандартное отклонение можно рассчитать по следующему алгоритму:

1. Сначала - вычисление среднего арифметического выборки данных.
2. Затем нужно вычесть среднее арифметическое от каждого элемента выборки.
3. Каждую полученную разницу следует возвести в квадрат.
4. Сложить все квадраты разниц, полученные в пункте 3.
5. Поделить сумму квадратов на количество элементов выборки.
6. Теперь из этого частного нужно извлечь квадратный корень.

Результат является стандартным отклонением.

Стандартное отклонение.

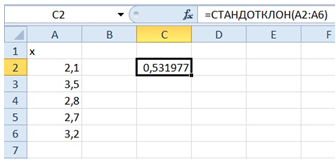
Дисперсия.

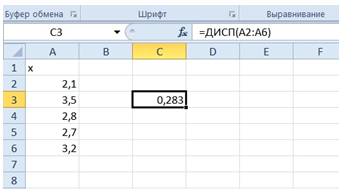
3. Сгенерируйте распределенную по закону Пуассона случайную величину
с лямбда равным 4. (N=50)

Постройте гистограмму, иллюстрирующую плотность распределения.

Ответ:

 

 

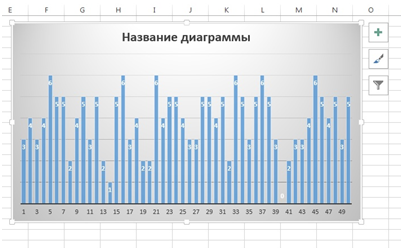
4. Что показывает коэффициент корреляции, какие значения он может принимать?

Ответ:

Величина влияния фактора на исследуемый отклик может быть оценена при помощи коэффициента линейной парной корреляции, характеризующего тесноту (силу) линейной связи между двумя переменными.

изменяется в диапазоне от –1 до +1. Положительное значение свидетельствует о прямой линейной связи, отрицательное – об обратной. Чем ближе абсолютное значение коэффициента к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент по абсолютной величине превышает 0,7, и слабая, если он менее 0,3.

 

5. Даны две выборки случайных величин. Посчитайте их к-т корреляции, сделайте вывод о степени их коррелированности.

X	40	55	50	47,5	52,5
Y	35	50	55	30	38

Ответ:

 

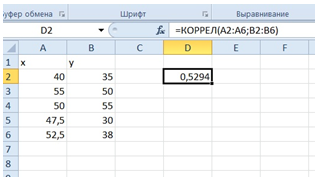
Коэффициент корреляции приближен к 1, следовательно, существует сильная связь. 

 

6. Для чего применяется регрессионный анализ? При каких результатах корреляционного анализа есть смысл проводить регрессионный анализ? Перечислите 4 предпосылки регрессионного анализа, напишите модель однофакторного регрессионного анализа.

Ответ:

Регрессионный анализ - способ моделирования измеряемых данных и исследования их параметров. Данные состоят из пар значений зависимой переменной (переменной отклика) и независящей переменной (объясняющей переменной). Регрессионная модель есть функция независящей переменной и характеристик с добавленной случайной переменной. Регрессионный анализ именуют главным способом современной математической статистики для выявления неявных и завуалированных связей меж данными наблюдений. Регрессионный и корреляционный анализы - это эффективные методы, которые разрешают анализировать значительные объемы информации с целью исследования вероятной взаимосвязи двух и больше переменных. В регрессивном анализе рассматривается связь между одной переменной, которая называется зависимой переменной, или признаком, и несколькими другими, которые называются независимыми переменными. Поскольку целью регрессионного анализа есть выявление влияния переменных X на значение переменной Y, последнюю еще называют откликом, или результативным фактором, а переменные x - факторами, которые влияют на отклик.С помощью регрессии определяются аналитические зависимости между переменными, а через корреляционный анализ - сила связи между факторами и откликом.Именно поэтому, что основные статистические проблемы регрессионного анализа решаются анализом корреляций, методы регрессионного и корреляционного анализа тесно связанные между собою.Применение метода наименьших квадратов для определения параметров регрессии предполагает выполнение некоторых предпосылок.

Отметим наиболее существенные из них.

Предпосылка 1. При нахождении оценок переменной у предполагается существование зависимости переменной у только от тех объясняющих переменных, которые вошли в модель (регрессию). Влияние прочих факторов и случайностей учитывается случайной возмущающей переменной z. При этом полагаем, что для фиксированных значений переменных х_i,  среднее значение переменной z равно нулю.

Предпосылка 2. Предполагается, что влияние неучтенных факторов постоянно. Так, при рассмотрении временных рядов в различные периоды эти неучтенные факторы оказывают одинаковое влияние.

Предпосылка 3. Отсутствует автокорреляция между возмущающими переменными z.

Предпосылка 4. Число наблюдений должно превышать число параметров регрессии, иначе невозможна оценка этих параметров.

 

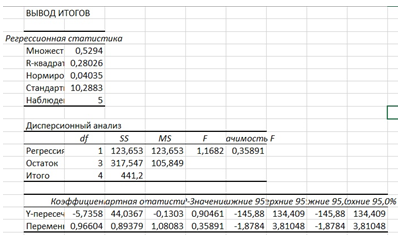
7. Проведите регрессионный анализ для данных из вопроса №5, взяв зависимой переменной Y, зависимой - X. Напишите уравнение регрессии и значение R^2.

Ответ:

R²=0,280264801

Y= -5.7358+0.96604x

 

8. Проведите двухфакторный регрессионный анализ взяв зависимой переменной Y.

Y	24,5	12,1	18,7	15,1	15,1
X1	10,1	4,5	8,7	7	10,2
X2	15,2	7,7	9,2	8,3	5,3

Ответ:

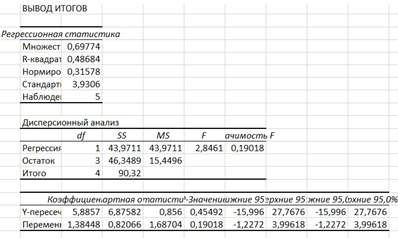
По итогам регрессии можно сделать вывод о высокой значимости модели, так как коэффициент детерминации равен 0,48, т.е. 48%. Также можно отметить, что значение F > Fкритерия, следовательно, имеет место влияние фактора.

 

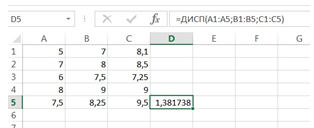
9. Расскажите цель применения дисперсионного анализа. Как должны соотносится межгрупповая и внутригрупповая дисперсия при наличии влияния фактора? Проведите дисперсионный анализ по следующим данным:

Отсутствие фактора:	5	7	6	8	7,5
Слабая степень  влияния фактора:	7	8	7,5	9	8,25
Сильная степень влияния фактора:	8,1	8,5	7,25	9	9,5

Подтверждается ли влияние фактора с уровнем значимости 0,05? С каким уровнем значимости присутствует влияние исследуемого фактора?

Ответ:

Основной целью дисперсионного анализа является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий. Разделение общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений).

Межгрупповых дисперсия - это средний квадрат отклонений групповых средних относительно общего

Среднего внутригрупповых дисперсия - это средняя арифметическая частных (групповых) дисперсий, взвешенная объемам групп.

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---