Контрольная работа по Методам оптимальных решений Вариант №3

Тема: Контрольная работа по Методам оптимальных решений Вариант №3

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 58.64K | Скачано: 253 | Добавлен 31.10.15 в 11:03 | Рейтинг: +1 | Еще Контрольные работы

Вуз: не указан

Формулы и рисунке смотрите в файле!

Задания:

1. Для транспортной задачи (открытая модель) найти оптимальный план перевозок.

	В1	В2	В3	В4	ai
A1	3	2	5	4	17
A2	2	1	4	3	16
A3	3	4	2	2	9
bj	9	11	13	7

2. Найти Парето-оптимальную границу.



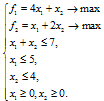
3. Найти седловую точку в игре с матрицей выигрышей А:



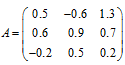
4. Необходимо распределить средства в размере   в течении 3-х лет между двумя предприятиями. Средства  , выделяемые 1 предприятию, приносят в конце года доход   и возвращаются в размере  . Средства  , вложенные во второе предприятие, соответственно, приносят доход   и возвращаются в размере  . В 1 год выделенные средства распределяются полностью, а в следующие годы полностью распределяются возвращенные средства за предыдущий год. Сколько средств нужно выделять каждому предприятию в начале года, чтобы суммарный доход был максимальный за все 3 года.

1. Для транспортной задачи (открытая модель) найти оптимальный план перевозок.

	В1	В2	В3	В4	ai
A1	3	2	5	4	17
A2	2	1	4	3	16
A3	3	4	2	2	9
bj	9	11	13	7

∑a = 17 + 16 + 9 = 42

∑b = 9 + 11 + 13 + 7 = 40

Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 2 (42—40). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.

	В1	В2	В3	В4	В5	ai
A1	3	2	5	4	0	17
A2	2	1	4	3	0	16
A3	3	4	2	2	0	9
bj	9	11	13	7	2

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку, и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен 1. Для этого элемента запасы равны 16, потребности 11. Поскольку минимальным является 11, то вычитаем его.

x₂₂ = min(16,11) = 11.

3	x	5	4	0	17
2	1	4	3	0	16 - 11 = 5
3	x	2	2	0	9
9	11 - 11 = 0	13	7	2	0

 Искомый элемент равен 2. Для этого элемента запасы равны 5, потребности 9. Поскольку минимальным является 5, то вычитаем его.  x₂₁ = min(5,9) = 5.

3	x	5	4	0	17
2	1	x	x	x	5 - 5 = 0
3	x	2	2	0	9
9 - 5 = 4	0	13	7	2	0

Искомый элемент равен 2. Для этого элемента запасы равны 9, потребности 13. Поскольку минимальным является 9, то вычитаем его.       x₃₃ = min(9,13) = 9.

3	x	5	4	0	17
2	1	x	x	x	0
x	x	2	x	x	9 - 9 = 0
4	0	13 - 9 = 4	7	2	0

Искомый элемент равен 3. Для этого элемента запасы равны 17, потребности 4. Поскольку минимальным является 4, то вычитаем его.       x₁₁ = min(17,4) = 4.

3	x	5	4	0	17 - 4 = 13
2	1	x	x	x	0
x	x	2	x	x	0
4 - 4 = 0	0	4	7	2	0

Искомый элемент равен 4. Для этого элемента запасы равны 13, потребности 7. Поскольку минимальным является 7, то вычитаем его.       x₁₄ = min(13,7) = 7.

3	x	5	4	0	13 - 7 = 6
2	1	x	x	x	0
x	x	2	x	x	0
0	0	4	7 - 7 = 0	2	0

Искомый элемент равен 5. Для этого элемента запасы равны 6, потребности 4. Поскольку минимальным является 4, то вычитаем его.        x₁₃ = min(6,4) = 4.

3	x	5	4	0	6 - 4 = 2
2	1	x	x	x	0
x	x	2	x	x	0
0	0	4 - 4 = 0	0	2	0

Искомый элемент равен 0. Для этого элемента запасы равны 2, потребности 2. Поскольку минимальным является 2, то вычитаем его.      x₁₅ = min(2,2) = 2.

3	x	5	4	0	2 - 2 = 0
2	1	x	x	x	0
x	x	2	x	x	0
0	0	0	0	2 - 2 = 0	0

	В1	В2	В3	В4	В5	ai
A1	3[4]	2	5[4]	4[7]	0[2]	17
A2	2[5]	1[11]	4	3	0	16
A3	3	4	2[9]	2	0	9
bj	9	11	13	7	2

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена.План является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 3*4 + 5*4 + 4*7 + 0*2 + 2*5 + 1*11 + 2*9  = 99

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалыu_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 3; 0 + v₁ = 3; v₁ = 3;     u₂ + v₁ = 2; 3 + u₂ = 2; u₂ = -1;

u₂ + v₂ = 1; -1 + v₂ = 1; v₂ = 2;    u₁ + v₃ = 5; 0 + v₃ = 5; v₃ = 5;

u₃ + v₃ = 2; 5 + u₃ = 2; u₃ = -3;    u₁ + v₄ = 4; 0 + v₄ = 4; v₄ = 4;

u₁ + v₅ = 0; 0 + v₅ = 0; v₅ = 0 ;

	v1=3	v2=2	v3=5	v4=4	v5=0
u1=0	3[4]	2	5[4]	4[7]	0[2]
u2=-1	2[5]	1[11]	4	3	0
u3=-3	3	4	2[9]	2	0

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Минимальные затраты составят: F(x) = 3*4 + 5*4 + 4*7 + 0*2 + 2*5 + 1*11 + 2*9  = 99

Анализ оптимального плана.

Из 1-го склада необходимо груз направить в 1-й магазин (4), в 3-й магазин (4), в 4-й магазин (7)

Из 2-го склада необходимо груз направить в 1-й магазин (5), в 2-й магазин (11)

Из 3-го склада необходимо весь груз направить в 3-й магазин

На 1-ом складе остался невостребованным груз в количестве 2 ед.

Оптимальный план является вырожденным, так как базисная переменная x₁₅=0.

2. Найти Парето-оптимальную границу.

 

Область допустимых решений D задается системой неравенств задается системой неравенств:

 

Постоим данную область. 

В качестве допустимого множества получаем область ОАВСD с угловыми точками О(0;0), А(0;4), В(3;4), С(5;2), D(5;0).

Для функций f1 и f2 построим линии уровня ( f1=const, f2=const) как прямые, перпендикулярные соответствующим векторам нормали 1n =(4;1) и 2 n =(1;2). Каждая из этих линий уровня разбивает плоскость XOY на 2 полуплоскости. Рассмотрим те из них Пi, которые содержат соответствующий вектор нормали (вектор градиента целевой функции). Пусть П=П1∩П2. Перемещая область П по границе множества D легко определить, что Парето-эффективной границей будет отрезок [BC], т.е. множество точек (1-t)(3;4)+t(5;2)=(3+2t; 4-2t), t‎ [0;1]

3. Найти седловую точку в игре с матрицей выигрышей А:

 

Для нахождения нижней цены игры найдем минимальные значения каждой строки матрицы и выберем среди них наибольшее.

                                                = -0.6

                                                = 0.6

                                                = -0.2

                                                =0.6

Для нахождения верхней цены игры найдем максимальное значение в каждом столбце и выберем среди них наименьшее.

                                                = 0.6

                                                = 0.9

                                                = 1.3

                                                = 0.6

Так как  , то цена игры v=0.6, и она достигается на  паре стратегий (А2; В1).

Седловая точка – (А2; В1).

4. Необходимо распределить средства в размере  в течении 3-х лет между двумя предприятиями. Средства , выделяемые 1 предприятию, приносят в конце года доход  и возвращаются в размере . Средства , вложенные во второе предприятие, соответственно, приносят доход  и возвращаются в размере . В 1 год выделенные средства распределяются полностью, а в следующие годы полностью распределяются возвращенные средства за предыдущий год. Сколько средств нужно выделять каждому предприятию в начале года, чтобы суммарный доход был максимальный за все 3 года.

n=3

Показатель эффективности k-го шага равен:

F_k = 0.3x_k + 0.7(e^k-1-x_k) = -0.4x_k + 0.7e^k-1

уравнение состояния принимает вид:

e_k = 0.4x_k + 0.6(e^k-1-x_k) = -0.2x_k + 0.6e^k-1

Тогда рекуррентные соотношения Беллмана запишутся следующим образом:

F₃(e²) = max[-0.4x₃ + 0.7e²]

0 ≤ x₃ ≤ e²

F_k(e^k-1) = max[-0.4x_k + 0.7e^k-1 + F_k+1(-0.2x_k + 0.6e^k-1)]

k = 1,2

0 ≤ x_k ≤ e^k-1

Проведем этап условной оптимизации.

3-йшаг:

F₃(e²) = max[-0.4x₃ + 0.7e²] = 0.7e²

0 ≤ x₃ ≤ e²

Так как показатель эффективности F₃(e²) является линейной функцией относительно x₃ и эта переменная входит в выражение со знаком минус, то он достигает максимума в начале интервала 0 ≤ x₃ ≤ e², т.е. при x₃ = 0.

2-й шаг:

F₂(e¹) = max[-0.4x₂ + 0.7e¹ + F₃(-0.2x₂ + 0.6e¹)] = max[-0.4x₂ + 0.7e¹ + 0.7(-0.2x₂ + 0.6e¹)] = -0.54x₂ + 1.12e¹ = 1.12e¹

0 ≤ x₂ ≤ e¹

Так как показатель эффективности F₂(e¹) является линейной функцией относительно x₂ и эта переменная входит в выражение со знаком минус, то он достигает максимума в начале интервала 0 ≤ x₂ ≤ e¹, т.е. при x₂ = 0.

1-й шаг:

F₁(e⁰) = max[-0.4x₁ + 0.7e⁰ + F₂(-0.2x₁ + 0.6e⁰)] = max[-0.4x₁ + 0.7e⁰ + 1.12(-0.2x₁ + 0.6e⁰)] = -0.624x₁ + 1.372e⁰ = 1.372e⁰

0 ≤ x₁ ≤ e⁰

Так как показатель эффективности F₁(e⁰) является линейной функцией относительно x₁ и эта переменная входит в выражение со знаком минус, то он достигает максимума в начале интервала 0 ≤ x₁ ≤ e⁰, т.е. при x₁ = 0.

Этап безусловной оптимизации.

Так как e⁰ = 5000, то F_max = F₁(e⁰) = 6860 и x₁ = 0.

Так как e⁰ = 5000, то e¹ = -0.2*0 + 0.6*5000 = 3000 и x₁ = 0.

Так как e¹ = 3000, то e² = -0.2*0 + 0.6*3000 = 1800 и x₂ = 0.

Так как e² = 1800, то e³ = -0.2*0 + 0.6*1800 = 1080 и x₃ = 0.

В результате средства по годам (табл.) оптимальным образом распределяются так:

Период	Средства	Предприятие №1	Предприятие №2	Остаток	Доход
1	5000	0	5000	3000	3500
2	3000	0	3000	1800	2100
3	1800	0	1800	1080	1260
					6860

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---