На подсобном предприятии налажено изготовление двух видов продукции: А и В.

Тема: На подсобном предприятии налажено изготовление двух видов продукции: А и В.

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 148.63K | Скачано: 277 | Добавлен 15.04.15 в 12:26 | Рейтинг: +1 | Еще Контрольные работы

Вуз: не указан

Задание 1

На подсобном предприятии налажено изготовление двух видов продукции: А и В.  Для их производства используются материалы трех сортов.

На изготовление единицы изделия А расходуется соответственно  а₁ кг материала 1-го сорта, а₂ кг материала 2-го сорта,   а₃ кг материала 3-го сорта.

На изготовление единицы изделия В расходуется соответственно  в₁ кг материала 1-го сорта, в₂ кг материала 2-го сорта,  в₃ кг материала 3-го сорта.

Всего имеется с₁ , с₂ , с₃ , кг материалов соответственно 1-го сорта,  2-го сорта, 3-го сорта.

Реализация единицы продукции А  приносит прибыль   рублей, реализация единицы продукции В приносит прибыль  рублей.

1. Построить экономико-математическую модель задачи.
2. Определить симплексным методом, при каком объеме производства прибыль будет максимальной.
3. Проверить полученное решение графически.
4. Сделать экономический анализ решения.
5. Решить задачу в EXCEL с использованием надстройки «Поиск решения». Приложить распечатку результатов, проанализировать её.
6. Построить задачу, двойственную данной.
7. Получить решение двойственной задачи с помощью теорем двойственности

а1	а2	а3	в1	в2	в3	с1	с2	с3
51	63	210	91	76	49	640	700	1420	7	6

1. Построить экономико-математическую модель задачи.

Количество изделия А обозначим х₁, В — х₂.

Доход от реализации единицы продукции А составляет 7x₁ руб., продукции В  6x₂ руб., общий доход — соответственно:

 F = 7x₁+ 6x₂.

Поскольку предприятию нужно получить наибольшую прибыль, то ставится задача максимизации целевой функции

F = 7x₁+ 6x₂® max.

Количество материалов 1-го сорта ограничено - 640 кг., при этом их расходуется на производство продукции А  — 51x₁, на производство продукции В — 91x₂. Поскольку количество израсходованного материала не должно превышать его запаса, можно записать следующее ограничение:

51x₁+ 91x₂ £ 640.

Аналогично записываются ограничения для других ресурсов:

63x₁+ 76x₂ £ 700

210x₁+ 49x₂ £ 1420

Таким образом, экономико-математическая модель задачи выглядит следующим образом:

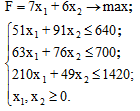
Целевая функция представляет собой общую прибыль от производства продукции. Ограничения отражают конечность запасов ресурсов на предприятии. Неотрицательность переменных следует из их смысла.

2. Определить симплексным методом, при каком объеме производства прибыль будет максимальной.

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных.

В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄. В 3-м неравенстве смысла (≤) вводим базисную переменную x₅. 

51x₁ + 91x₂ + 1x₃ + 0x₄ + 0x₅ = 640

63x₁ + 76x₂ + 0x₃ + 1x₄ + 0x₅ = 700

210x₁ + 49x₂ + 0x₃ + 0x₄ + 1x₅ = 1420

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных: x₃, x₄, x₅

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,640,700,1420)

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных: x₃, x₄, x₅

Полагая, что свободные переменные равны 0, получим первый опорный план:

X1 = (0,0,640,700,1420)

Базисное решение называется допустимым, если оно неотрицательно.

 

Базис	B	x1	x2	x3	x4	x5
x3	640	51	91	1	0	0
x4	700	63	76	0	1	0
x5	1420	210	49	0	0	1
F(X0)	0	-7	-6	0	0	0

Итерация №0.

Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Определение новой свободной переменной. Вычислим значения D_i по строкам как частное от деления: b_i / a_i1 и из них выберем наименьшее:

min (640 : 51 , 700 : 63 , 1420 : 210 ) = 6¹⁶/₂₁

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (210) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	min
x3	640	51	91	1	0	0	1228/51
x4	700	63	76	0	1	0	111/9
x5	1420	210	49	0	0	1	616/21
F(X1)	0	-7	-6	0	0	0	0

Пересчет симплекс-таблицы.

Формируем следующую часть симплексной таблицы.

Вместо переменной x₅ в план 1 войдет переменная x₁.

Строка, соответствующая переменной x₁ в плане 1, получена в результате деления всех элементов строки x₅ плана 0 на разрешающий элемент РЭ=210. На месте разрешающего элемента в плане 1 получаем 1.

В остальных клетках столбца x₁ плана 1 записываем нули.

Таким образом, в новом плане 1 заполнены строка x₁ и столбец x₁.

Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.

Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.

НЭ = СЭ - (А*В)/РЭ

СТЭ - элемент старого плана, РЭ - разрешающий элемент (210), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Представим расчет каждого элемента в виде таблицы:

B	x 1	x 2	x 3	x 4	x 5
640-(1420 • 51):210	51-(210 • 51):210	91-(49 • 51):210	1-(0 • 51):210	0-(0 • 51):210	0-(1 • 51):210
700-(1420 • 63):210	63-(210 • 63):210	76-(49 • 63):210	0-(0 • 63):210	1-(0 • 63):210	0-(1 • 63):210
1420 : 210	210 : 210	49 : 210	0 : 210	0 : 210	1 : 210
0-(1420 • -7):210	-7-(210 • -7):210	-6-(49 • -7):210	0-(0 • -7):210	0-(0 • -7):210	0-(1 • -7):210

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5
x3	2066/7	0	791/10	1	0	-17/70
x4	274	0	613/10	0	1	-3/10
x1	142/21	1	7/30	0	0	1/210
F(X1)	142/3	0	-131/30	0	0	1/30

Итерация №1.

Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Определение новой свободной переменной. Вычислим значения D_i по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее:

min (295¹/₇ : 79¹/₁₀ , 274 : 61³/₁₀ , 6¹⁶/₂₁ : ⁷/₃₀ ) = 3⁴⁰⁴⁹/₅₅₃₇

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (79¹/₁₀) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	min
x3	2951/7	0	791/10	1	0	-17/70	34049/5537
x4	274	0	613/10	0	1	-3/10	4288/613
x1	616/21	1	7/30	0	0	1/210	2848/49
F(X2)	471/3	0	-411/30	0	0	1/30	0

Пересчет симплекс-таблицы.

Формируем следующую часть симплексной таблицы.

Вместо переменной x₃ в план 2 войдет переменная x₂.

Строка, соответствующая переменной x₂ в плане 2, получена в результате деления всех элементов строки x₃ плана 1 на разрешающий элемент РЭ=79¹/₁₀

На месте разрешающего элемента в плане 2 получаем 1.

В остальных клетках столбца x₂ плана 2 записываем нули.

Таким образом, в новом плане 2 заполнены строка x₂ и столбец x₂.

Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.

Представим расчет каждого элемента в виде таблицы:

B	x 1	x 2	x 3	x 4	x 5
2951/7 : 791/10	0 : 791/10	791/10 : 791/10	1 : 791/10	0 : 791/10	-17/70 : 791/10
274-(2951/7 • 613/10):791/10	0-(0 • 613/10):791/10	613/10-(791/10 • 613/10):791/10	0-(1 • 613/10):791/10	1-(0 • 613/10):791/10	-3/10-(-17/70 • 613/10):791/10
616/21-(2951/7 • 7/30):791/10	1-(0 • 7/30):791/10	7/30-(791/10 • 7/30):791/10	0-(1 • 7/30):791/10	0-(0 • 7/30):791/10	1/210-(-17/70 • 7/30):791/10
471/3-(2951/7 • -411/30):791/10	0-(0 • -411/30):791/10	-411/30-(791/10 • -411/30):791/10	0-(1 • -411/30):791/10	0-(0 • -411/30):791/10	1/30-(-17/70 • -411/30):791/10

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5
x2	20660/5537	0	1	10/791	0	-17/5537
x4	250680/5537	0	0	-613/791	1	-619/5537
x1	4660/791	1	0	-1/339	0	13/2373
F(X2)	352300/5537	0	0	131/2373	0	331/16611

Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5
x2	20660/5537	0	1	10/791	0	-17/5537
x4	250680/5537	0	0	-613/791	1	-619/5537
x1	4660/791	1	0	-1/339	0	13/2373
F(X3)	352300/5537	0	0	131/2373	0	331/16611

Оптимальный план можно записать так:

x₂ = 250680/5337 (≈5,891)

x₁ = 4660/791 (≈3,731)

F(X) = 7·4660/791 + 6·250680/5337 = 352300/5337 (≈63,626)

3. Проверить полученное решение графически.

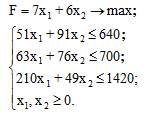
В первую очередь, найдем область допустимых решений, т.е. точки x₁ и x₂ , которые удовлетворяют системе ограничений.

По условию задачи x₁  0, x₂  0 ,т.е. мы рассматриваем только те точки, которые принадлежат первой четверти.

Построим область решений системы ограничений. Для этого рассмотрим равенства и построим их графики – прямые.

1) 51х₁ + 91х₂ ≤ 640

     51х₁ + 91х₂ = 640

х1	х2
0	7,03
15	-1,37

 

2)  63х₁ + 76х₂ ≤ 700

      63х₁ + 76х₂ = 700

х1	х2
0	9,21
15	-3,22

3) 210х₁ + 49х₂ ≤ 1420

     210х₁ + 49х₂ = 1420

х1	х2
0	28,98
15	-35,31

4) х₁ ³ 0

     х₁ = 0 – ось ОХ₂.

5) х₂ ³ 0

     х₂ = 0 – ось ОХ₁.

Сведем все полученные прямые на одном графике.

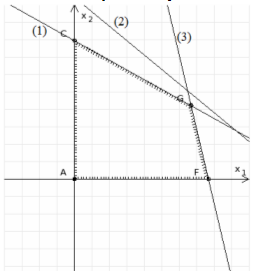
Для нахождения оптимального решения задачи изобразим графически функцию цели:

F (х) = n₁x₁ + n₂x₂

F(х) = 7х₁ + 6х₂

Для этого строим вектор N, начало которого в точке (0;0), а конец в точке (n₁;n₂).

n = (7; 6).

Значение функции z будет возрастать при перемещении прямой в направлении вектора ON.

Будем перемещать прямую, перпендикулярную вектору ON, до тех пор, пока она полностью не пройдет область допустимых решений.

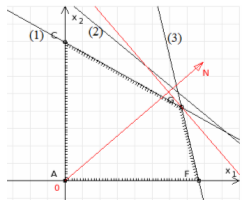
В нашем случае, касание прямой, перед выходом из области допустимых решений, произойдет в вершине G. В точке G значение функции z будет наибольшим.

Так как точка G получена в результате пересечения прямых(1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

51х₁ + 91х₂ = 640    

210х₁ + 49х₂ = 1420          

Решив систему уравнений, получим: x₁ = 5,8913, x₂ = 3,7313.
Откуда найдем максимальное значение целевой функции:
max F(X) = 7·5,8913 + 6·3,7313 = 63,6265

4. Сделать экономический анализ решения.

Полученное решение означает, что максимальную прибыль 63,626 руб. предприятие может получить при выпуске 5,8913 кг изделия А и 3,7313 кг изделия В.

Подставим оптимальный план прямой задачи в систему ограниченной математической модели:

51·5,891 + 91·3,731 = 640 = 640

63·5,891  + 76·3,731 = 654,726 < 700

210·5,891  + 49·3,731 = 1420 = 1420

1-ое ограничение прямой задачи выполняется как равенство. Это означает, что материалы 1-го сорта полностью используются в оптимальном плане. 

2-ое ограничение выполняется как строгое неравенство, т.е. материалы 2-го сорта израсходованы не полностью.

Неиспользованный экономический резерв составляет 45,274 (700-654,726).

Этот резерв не может быть использован в оптимальном плане, но указывает на возможность изменений в объекте моделирования (например, резерв ресурса можно продать).

3-ое ограничение прямой задачи выполняется как равенство. Это означает, что материалы 3-го сорта полностью используется в оптимальном плане.

5. Решить задачу в EXCEL с использованием надстройки «Поиск решения». Приложить распечатку результатов, проанализировать её.

Введем исходные данные в таблицу в Excel.

Целевая функция содержит формулу: = СУММПРОИЗВ(C$4:D$4;C5:D5).

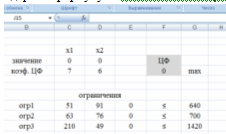
Выполним поиск решений с помощью надстройки Поиск решения.
Вызовем надстройку Поиск решения и заполним окно поиска.

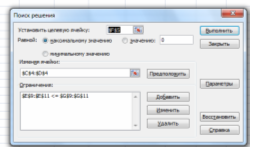
В графе ПАРАМЕТРЫ устанавливаем значения Линейная модель и Неотрицательное значение. Получаем следующие результаты решения

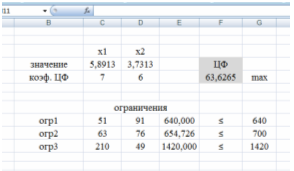
Полученное решение означает, что максимальную прибыль предприятие может получить при выпуске 5,8913 кг изделия А и 3,7313 кг изделия В. При этом для производства продукции нужно использовать 640 кг материала 1-го сорта, 654,726 кг материала 2-го сорта и 1420 кг 3-го сорта.

6. Построить задачу, двойственную данной.

Т.к. прямая задача является задачей максимизации, двойственная задача будет задачей минимизации.

В исходной задаче число ограничений три, поэтому в двойственной будет три переменных у₁, у₂, у₃.

В исходной задаче две переменные, поэтому в двойственной будет два ограничения.

Все ограничения исходной задачи – неравенства, поэтому на переменные  у₁, у₂, у₃ в двойственной задаче будет наложено условие неотрицательности: у₁, у₂, у₃  ≥ 0 

Составим расширенную матрицу системы.

Найдем матрицу Ат1, транспонированную к А1.

Так как  целевая функция двойственной задачи минимизируется, то все ограничения задачи должны иметь знак  >.   

Сформулируем двойственную задачу.

Целевая функция двойственной задачи:

 z (y) = 640y₁ + 700y₂ + 1420y₃ → min

Ограничения:

51y₁ + 63y₂ + 210y₃≥7

91y₁ + 76y₂ + 49y₃≥6

y₁ ≥ 0

y₂ ≥ 0

y₃ ≥ 0

7.Получить решение двойственной задачи с помощью теорем двойственности.

Воспользуемся теоремами двойственности для решения двойственной задачи:

1. Подставив компоненты оптимального плана исходной задачи в систему уравнений ограничений исходной задачи мы получили:

51·5,891 + 91·3,731 = 640 = 640

63·5,891  + 76·3,731 = 654,726 < 700

210·5,891  + 49·3,731 = 1420 = 1420

Из второго уравнения по первой части второй теоремы двойственности можно утверждать , т.к. второе ограничение исходной задачи при подстановке оптимального плана содержит знак < между правой и левой частью.

2. Т.к. и , то по второй части второй теоремы двойственности в первом и втором уравнениях ограничений двойственной задачи между правой и левой частью может быть поставлен знак равенства:

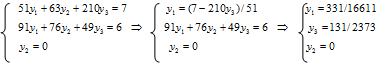
3. Рассчитаем целевую функцию двойственной задачи:

z (y) = 640·331/16611 + 700·0 + 1420·131/16611 = 352300/5537 (≈63,6265)

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---