Задача об оптимальном использовании ограниченных ресурсов

Тема: Задача об оптимальном использовании ограниченных ресурсов

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 761.85K | Скачано: 417 | Добавлен 27.10.14 в 20:03 | Рейтинг: 0 | Еще Контрольные работы

Вуз: не указан

ЗАДАЧА 1. Задача об оптимальном использовании ограниченных ресурсов

1. Постановка экономической задачи (исходные данные варианта)

Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 м древесины, а для изготовления одного стола — 7 м. На изготовление одного стула уходит 2 часа рабочего времени, а на изготовление стола — 8 часов. Каждый стул приносит 1 ден. ед. прибыли, а каждый стол — 3 ден. ед. Сколько стульев и сколько столов должна изготовить эта фирма для получения максимальной прибыли, если она располагает 200 м древесины и 400 часами рабочего времени?

2. Экономико-математическая модель задачи

ЭММ задачи:

Х₁ – количество столов

Х₂ – количество стульев

F=3X₁+X₂→max

Ограничения:

7Х₁+3Х₂<=200;

8Х₁+2Х₂<=400;

Х_1,2>=0.

3. Компьютерная технология получения оптимального решения

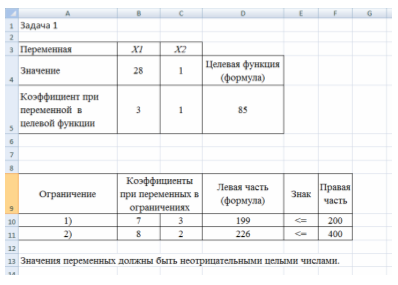
Данную задачу решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:

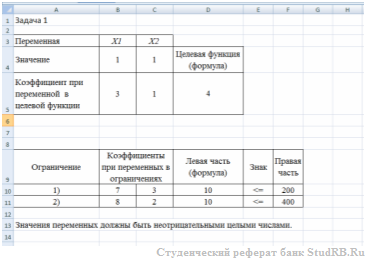
В ячейках В4:С4 находятся значения переменных х₁ и х₂ соответственно. Первоначально в них помещаются произвольные числа, например, единицы.

В ячейки В5:С5 помещаются коэффициенты при переменных в целевой функции задачи.

В ячейку D5 вводится выражение целевой функции с использованием встроенной функции «СУММПРОИЗВ». Аргументами этой функции являются вышеуказанные массивы ячеек B4:C4 и B5:C5. Формула в ячейке D5, таким образом, имеет вид: =СУММПРОИЗВ($B$4:$C$4;B5:C5).

В ячейки В10:С14 помещаются коэффициенты при переменных в ограничениях задачи.

В ячейки D10:D14 вводятся выражения левых частей ограничений также с использованием функции «СУММПРОИЗВ». Например, в ячейке D10 формула имеет вид: =СУММПРОИЗВ($B$4:$C$4;B10:C10).

В ячейках Е10:Е11для удобства и наглядности указываются знаки в ограничениях.

В ячейки F10:F11 вводятся значения правых частей ограничений.

Исходный рабочий лист EXCEL, таким образом, имеет вид:

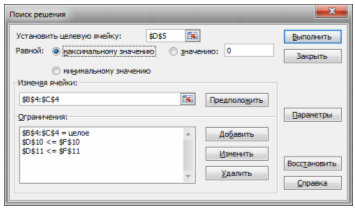
Для решения задачи оптимизации запускается надстройка «Поиск решения» (меню «Сервис») и заполняются все необходимые поля в панели надстройки:

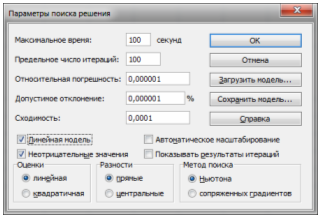
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных:

4. Решение задачи

После запуска надстройки «Поиск решения» на выполнение было получено сообщение об успешном решении задачи оптимизации:

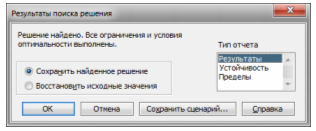
В окне «Тип отчета» выбирается пункт «Результаты».

Рабочий лист EXCEL, содержащий результаты решения, имеет вид:

5. Экономический вывод:

Полученное решение означает, что максимальный доход 85 ден.ед. фирма может получить при выпуске 28 столов и 1 стула. При этом ресурсы будут использованы не полностью: древесины используется 199 м, а времени потратиться вместо 400, 226 часов.

ЗАДАЧА 2. Задача о назначениях

1. Постановка экономической задачи (исходные данные варианта)

Мастер должен назначить на 10 типовых операций 12 рабочих. Данные о времени, которое затрачивают рабочие на выполнение каждой операции, приведены ниже в таблице (матрица эффективностей назначений):

Операции Рабочие	О1	О2	О3	О4	О5	О6	О7	О8	О9	О10
Р1	29	31	16	16	17	34	20	28	16	13
Р2	29	25	22	30	24	31	37	23	16	27
Р3	27	32	–	14	34	30	27	16	19	17
Р4	21	35	–	32	31	28	30	29	31	16
Р5	21	36	–	14	24	30	21	28	29	27
Р6	28	35	25	30	22	16	–	18	25	18
Р7	27	34	33	26	14	19	18	37	19	16
Р8	27	34	27	30	37	37	26	22	35	33
Р9	16	26	18	26	16	20	31	34	28	29
Р10	16	22	33	22	21	19	19	37	36	24
Р11	26	35	13	14	17	36	17	17	25	21
Р12	34	25	19	14	36	36	17	36	26	33

 В матрице эффективностей назначений проставлен запрет «-», если рабочий не может выполнять соответствующую операцию.

Сформировать план назначений рабочих по операциям, при котором суммарное время на выполнение работ будет минимально.

2. Экономико-математическая модель задачи

Данная задача является задачей о назначениях и реализуется как частный случай транспортной задачи. Видно, что число рабочих (12) превышает количество операций, которое они должны выполнить (10). Следовательно, задача является открытой, и решать ее целесообразно путем приведения к закрытой задаче, для чего вводятся две фиктивные операции — О11 и О12. Время на выполнение фиктивных операций равно нулю, так как они фактически не выполняются.

Представим исходные данные закрытой задачи в виде таблицы:

Операции Рабочие	О1	О2	О3	О4	О5	О6	О7	О8	О9	О10	О11	О12
Р1	29	31	16	16	17	34	20	28	16	13
Р2	29	25	22	30	24	31	37	23	16	27
Р3	27	32	1000	14	34	30	27	16	19	17
Р4	21	35	1000	32	31	28	30	29	31	16
Р5	21	36	1000	14	24	30	21	28	29	27
Р6	28	35	25	30	22	16	1000	18	25	18
Р7	27	34	33	26	14	19	18	37	19	16
Р8	27	34	27	30	37	37	26	22	35	33
Р9	16	26	18	26	16	20	31	34	28	29
Р10	16	22	33	22	21	19	19	37	36	24
Р11	26	35	13	14	17	36	17	17	25	21
Р12	34	25	19	14	36	36	17	36	26	33

В ячейках с заливкой находятся затраты времени c_ij на выполнение i–м рабочим (i=1, …, 12) j–й операции (j=1, …, 12). В ячейки, в которых был знак «–», вместо него помещены числа, существенно превышающие другие затраты времени (1000), чтобы при решении задачи соответствующие значения переменных оказались заведомо равными нулю.

Обозначим через x_ij факт назначения i–го рабочего на выполнение j–й операции (1 — если рабочий назначен, 0 — если не назначен). Математическая модель задачи имеет вид:

Найти такие значения x_ij, чтобы суммарное время на выполнение всех работ было наименьшим:

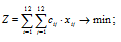
и при этом:

· каждый рабочий должен быть назначен только на одну операцию:

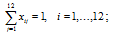
· на каждую операцию должен быть назначен только один рабочий:

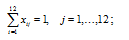
· переменные задачи являются двоичными:

3. Компьютерная технология получения оптимального решения

Данную задачу решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:

В ячейки B5:M11 вводятся затраты времени, необходимого рабочим на выполнение операций;

В ячейках B20:M31 находятся значения переменных x_ij. Первоначально в них помещаются произвольные числа, например, единицы.

В ячейки N20:N31 вводятся формулы для расчета сумм значений переменных в соответствующих строках. Например, в ячейке N20 формула имеет вид: =СУММ(B20:H20).

В ячейки B32:H32 вводятся формулы для расчета сумм значений переменных в соответствующих столбцах. Например, в ячейке B32 формула имеет вид: =СУММ(B20:B31).

В ячейку B34 вводится выражение целевой функции задачи с использованием встроенной функции EXCEL «СУММПРОИЗВ». Аргументами этой функции являются блоки ячеек, содержащие затраты времени и значения переменных: =СУММПРОИЗВ(B5:M16;B20:M31).

Лист исходных данных, таким образом, имеет вид:

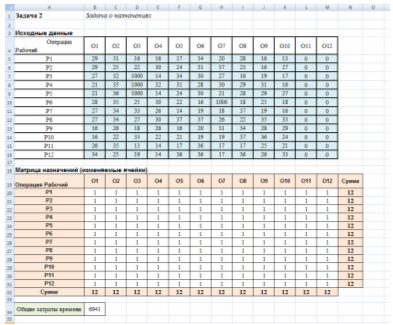
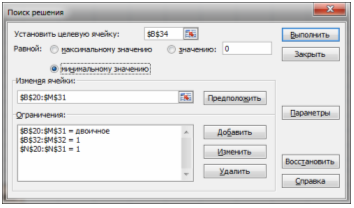
После ввода исходных данных запускается надстройка «Поиск решения» (меню «Сервис» ® «Поиск решения…») и заполняются необходимые поля в панели надстройки:

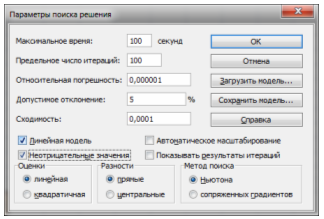
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных:

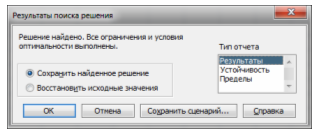
4. Решение задачи на ЭВМ

После запуска надстройки «Поиск решения» на выполнение было получено сообщение об успешном решении задачи оптимизации:

В окне «Тип отчета» выбираем пункт «Результаты».

Рабочий лист EXCEL, содержащий результаты решения имеет вид:

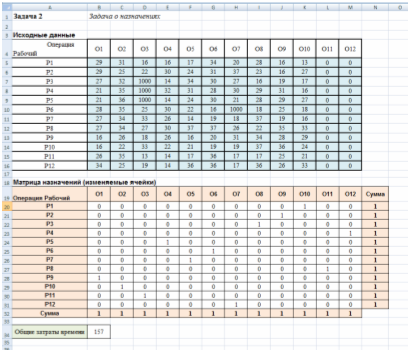
5. Предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению

Таким образом, чтобы суммарные затраты времени на выполнение операций были наименьшими, следует назначить:

рабочего 1 на выполнение операции 10;

рабочего 2 на выполнение операции 9;

рабочего 3 на выполнение операции 8;

рабочего 4 на выполнение фиктивной операции 12;

рабочего 5 на выполнение операции 4;

рабочего 6 на выполнение операции 6;

рабочего 7 на выполнение фиктивной операции 5;

рабочего 8 на выполнение фиктивной операции 11;

рабочего 9 на выполнение операции 1;

рабочего 10 на выполнение операции 2;

рабочего 11 на выполнение операции 3;

рабочего 12 на выполнение операции 7.

Рабочие 4 и 8, назначенные на выполнение фиктивных операций, фактически не работают.

Суммарное время на выполнение всех операций составит 157 ч.

Чтобы полностью ознакомиться с контрольной, скачайте файл!

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---