Контрольная по методам оптимальных решений

Тема: Контрольная по методам оптимальных решений

Раздел: Бесплатные рефераты по методам оптимальных решений

Тип: Контрольная работа | Размер: 516.57K | Скачано: 502 | Добавлен 23.04.14 в 11:33 | Рейтинг: -1 | Еще Контрольные работы

Вуз: не указан

Содержание

Задание 1.    3

Задание 2.    14

Задание 3.    18

Задание 4.    19

Задание 5.    23

Список литературы    26

 

Задание 1.

В предлагаемой альтернативной хозяйственной ситуации получите с помощью средств MS Excel (надстройка Поиск решения) оптимальный план производства продукции, проведите экономико-математический анализ оптимального плана с помощью двойственных оценок.

1.4. Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена реализации единицы каждого вида продукции приведены в таблице:

Вид сырья	Нормы расхода сырья на единицу продукции			Запасы сырья
	А	Б	В
I	4	2	1	180
II	3	1	2	210
III	1	2	3	244
Цена единицы продукции	10	14	12	-

? 1. Сформулируйте прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получите оптимальный план выпуска продукции.

2. Сформулируйте двойственную задачу и найдите ее оптимальный план (двойственные оценки).

3. Поясните нулевые значения переменных в оптимальном плане.

4. На основе свойств двойственных оценок и теорем двойственности:

а) проанализируйте использование ресурсов в оптимальном плане исходной задачи;

б) определите, как изменятся выручка и план выпуска продукции при увеличении каждого из запасов сырья первого и третьего видов на 4 единицы;

в) оцените целесообразность включения в план выпуска продукции изделия «Г» ценой 13 единиц, на изготовление которого расходуется 1, 3 и 2 единицы каждого вида сырья, и изделия «Д» ценой 12 единиц, на изготовление которого расходуется по 2 единицы каждого вида сырья.

Решение

1. Обозначим через х_j , j=1,3 - объем выпуска продукции j-го вида и запишем математическую модель задачи критерию «максимум прибыли»:

max f(X) = 10x₁+14x₂+12x₃

 

4x₁+2x₂+x₃ ≤ 180

3x₁+x₂+2x₃ ≤ 210

x₁+2x₂+3x₃ ≤ 244

х_j ≥ 0, j=1,3

В этой модели функциональные ограничения отражают условия ограниченности объемов используемых в производстве ресурсов.

Найдем оптимальный план задачи с помощью надстройки Excel Поиск решения.

1) Для задачи подготовим форму для ввода условий (см. рис. 1)

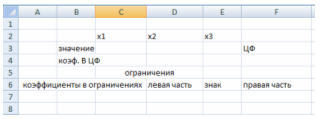
Рис. 1. Введена форма для ввода данных.

2) В нашей задаче оптимальные значения вектора Х=(Х₁, Х₂, Х₃) будут помещены в ячейках С3:E3, оптимальное значение целевой функции – в ячейке F4.

3) Введем исходные данные в созданную форму. Получим результат, показанный на рис. 2.

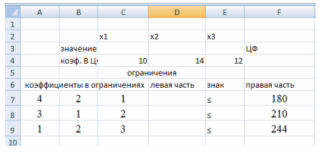
Рис. 2. Данные введены.

4) Введем зависимость для целевой функции (обозначим через М1 следующее действие – «один щелчок левой кнопкой мыши»):

• Курсор в F4.
• Курсор на кнопку Мастер функций.
• М1. На экране диалоговое окно Мастер функций шаг 1 из 2.
• Курсор в окно Категория на категорию Математические.
•  
• Курсор в окно Функции на СУММПРОИЗВ.
•  
• В массив 1 ввести (адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести) С$3:E$3.
• В массив 2 ввести С$4:E$4.
• Готово. На экране: в F4 введена функция, как показано на рис. 3.

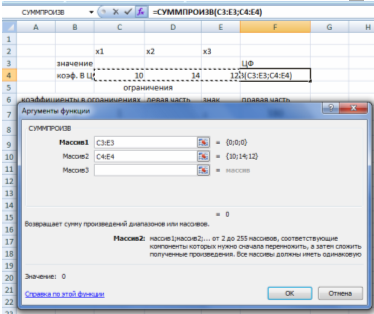
  Рис. 3. Вводится функция для вычисления целевой функции.

5) Введем зависимость для левых частей ограничений:

• Курсор в D7: СУММПРОИЗВ(С3:E3;A7:C7).
• Курсор в D8: СУММПРОИЗВ(С3:E3;A8:C8).
• Курсор в D9: СУММПРОИЗВ(С3:E3;A9:C9).

На этом ввод зависимостей закончен.

Запуск  Поиска решения

После выбора команд СервисÞПоиск решения появится диалоговое окно Поиск решения.

6) Назначение целевой функции (установить целевую ячейку).

• Курсор в поле «Установить целевую ячейку».
• Ввести адрес $F$4.
• Ввести направление целевой функции: Максимальному значению.

Ввести адрес искомых переменных:

• Курсор в поле «Изменяя ячейки».
• Ввести адреса $C$3:$E$3.

7) Ввод ограничений.

• Курсор в поле «Добавить». Появится диалоговое окно Добавление ограничения (рис. 4).

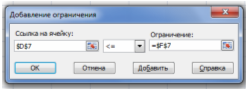
Рис. 4. Ввод правых и левых частей ограничений.

• В поле «Ссылка на ячейку» ввести адрес $D$7.
• Ввести знак ограничения <=.
• Курсор в правое окно.
• Ввести адрес $F$7.
• . На экране опять диалоговое окно Добавление ограничения.
• Ввести второе ограничение.
• .я На экране опять диалоговое окно Добавление ограничения.
• Ввести третьеограничение ОК.

На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 5).

8) Ввод параметров для решения ЗЛП (рис. 6.).

• Открыть окно Параметры поиска решения.
• Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.
• Установить флажок Неотрицательные значения.
• ОК. (На экране диалоговое окно Поиска решения).
• Выполнить. (На экране диалоговое окно Результаты поиска решения – рис. 7).

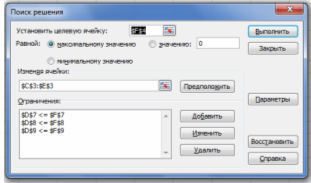
Рис. 5. Введены все условия для решения задачи.

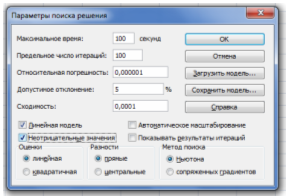
Рис. 6. Ввод параметров.

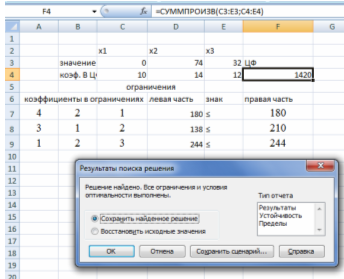
Рис. 7. Решение.

Рис. 7. Решение.

Полученное решение означает, что максимум функции равен 1420, при Х₁=0, Х₂=74 и Х₃=32.

Проверим, как удовлетворяется система функциональных ограничений оптимальным планом X* = (x₁ = 0, x₂ = 74, х₃ = 32):

4*0+2*74+1*32 = 180 = 180

3*0+1*74+2*32 = 138 < 210                                                     (*)

1*0+2*74+3*32 = 244 = 244

Значение целевой функции на этом плане равно

f(X^*) = 10*0+14*74+12*32 = 1420

2. Двойственная задача имеет вид:

min g(Y) = 180y₁+210y₂+244y₃

4y₁+3y₂+y₃ ≥ 10

2y₁+y₂+2у₃ ≥ 14

y₁+2y₂+3y₃ ≥ 12

y_1,2,3 ≥ 0.

Для нахождения оценок y₁, у₂, у₃ используем вторую теорему двойственности. Поскольку второе ограничение в (*) выполняется как строгое неравенство, то у₂^* = 0. Так как :х₂ > 0 и х₃ > 0, то:

2y₁^*+y₂^*+2y₃^* = 14

y₁^*+2y₂^*+3y₃^* = 12.

Итак, для получения двойственных оценок имеем систему линейных уравнений:

у₂^* = 0

2y₁^*+y₂^*+2y₃^* = 14

y₁^*+2y₂^*+3y₃^* = 12.

т.е. у₁^* = 4,5; y₂^* = 0; y₃^* = 2,5.

Вычислим значение целевой функции двойственной задачи:

g(Y^*) = 180*4,5+210*0+244*2,5 = 1420, т.е. f(X*) = g(Y*) = 1420

По первой теореме двойственности мы можем утверждать, что действительно найдены оптимальные значения двойственных переменных.

3. Нулевое значение переменной х₁ в оптимальном плане означает, что изготовление этого вида продукции не выгодно, т.к. цена реализации этого вида продукции низкая, а нормы расхода сырья на изготовление одного изделия этого вида высокие.

4. Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем недефицитны (избыточны).

В примере недефицитным ресурсом является II тип сырья, поскольку у₂= 0.

Острее ощущается дефицитность ресурса I тип сырья (у₁ = 4,5) - он более дефицитен, чем ресурс III тип сырья (у₃ = 2,5).

Предположим, что запасы сырья I вида увеличили на 4 ед., т. е. теперь они составляют 180 + 4 = 184 единиц, и запасы сырья III вида увеличили на 4 ед., т. е. теперь они составляют 244 + 4 = 248 единиц. Из теоремы об оценках Δf(X) = y_i • Δb_i, известно, что колебание величины b_i приводит к увеличению или уменьшению f(X). Оно определяется величиной y_i в случае, когда при изменении величин b_i, значения переменных y_i в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы.

Пределы уменьшения (нижняя граница) определяются по тем x_k (k = 1,..., т), для которых соответствующие d_ki >0:

Δb_i^(-) = min{x_k/d_ki} для d_ki > 0                             (1)

Пределы увеличения (верхняя граница) определяются по тем x_k, для которых    d_ki < 0:

Δb_i⁽⁺⁾ =| max{x_k/d_ki} | для d_ki < 0                          (2)

Определим интервалы устойчивости двойственных оценок в примере. Матрица А имеет вид:

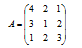
После приведения задачи к канонической форме матрица А примет следующий вид:

С ненулевыми значениями в оптимальный план вошли x₂* = 74, x₃* = 32 и х₅* = 72 (из (*) 210-138=72), следовательно, матрица А* будет составлена из второго, третьего и пятого столбцов матрицы А:

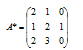
Для вычисления интервалов устойчивости необходимо найти матрицу D = А*^-1 (обратную матрицу матрицы А*):

При вычислении интервалов устойчивости по формулам (1) и (2) примем

х₂* = 74 = x_k=1, х₃* = 32 = x_k=2 и х₅^* = 72 = х_k=3.

Интервалы устойчивости первого ресурса — «запасы сырья I типа»:

Δb₁^(-) = min{x₁/d₁₁, x₃/d₃₁} = 74:3/4 = 296/3

Δb₁⁽⁺⁾ = | max{x₂/d₂₁} | = | 32:(-1/2) | = | -64 | = 64

b₁ = {b₁ - Δb₁^(-) ; b₁ + Δb₁⁽⁺⁾} = {180 – 296/3; 180+64} = {244/3; 244}.

При изменении запасов сырья I типа в пределах от 244/3 до 244 единиц двойственная оценка его не изменится.

Интервалы устойчивости второго ресурса — «запасы сырья II типа»: этот ресурс в оптимальном плане используется не полностью и поэтому не имеет верхней границы интервалов устойчивости; нижняя граница определяется следующим образом:

Δb₂^(-) = min{x₃/d₃₂} = 72:1 = 72

b₂ = {b₂ – Δb₂^(-) ; b₂ + Δb₂⁽⁺⁾ } = {210-72;210} = {138; 210}.

Интервалы устойчивости третьего ресурса — «запасы сырья III типа»:

Δb₃^(-) = min{x₂/d₂₃} = 74:1/2 = 148

Δb₃⁽⁺⁾ = |mах{x₁/d₁₃, x₃/d₃₃}| = | mах{-74:1/4, -72:3/4}| = |-96| = 96

b₃ = {b₃ – Δb₃^(-) ; b₃ + Δb₃⁽⁺⁾} = {244-148; 244+96} = {96; 340}.

В нашем примере определим величину изменения объема прибыли от реализации продукции при увеличении запасов I и III типа сырья на 4 ед. каждого. Эти изменения находятся в интервалах устойчивости двойственных оценок (244/3<184<244; 96<248<340), поэтому можно воспользоваться теоремой об оценках:

Δf(X) = 4·4,5+4·2,5 = 28

Объем стоимости выпускаемой продукции увеличится на 28 единиц.

Такой же ответ мы получили бы, если бы решили симплексным методом задачу с новыми ограничениями по запасам сырья I и III типа. Новый оптимальный план:    Х*=(0, 76, 32, 0, 70, 0)

f(X) = 0*10+76*14+32*12 = 1448,

Δf(X) = 1448-1420 = 28

Структурных сдвигов в программе не произошло, но значения переменных в плане изменились. Значение целевой функции при новых ограничениях увеличится на 28 единиц.

Двойственные оценки служат инструментом определения эффективности отдельных хозяйственных решений (технологических способов), с их помощью можно определять выгодность производства новых изделий, эффективность новых технологических способов:

если Δ _j = ∑ a_ij y_i^* - c_j ≤ 0 - выгодно,

если Δ _j > 0 – невыгодно.

Определим целесообразность включения в план изделия «Г» ценой 13 ед., на изготовление которого расходуется 1, 3 и 2 ед. каждого вида сырья соответственно.

Δ ₄ = 1*4,5 + 3*0 + 2*2,5– 13 = -3,5 < 0, т.е. включение в план изделия «Г» ценой 13 ед. выгодно.

Определим целесообразность включения в план изделия «Д» ценой 12 ед., на изготовление которого расходуется по две единицы каждого вида сырья.

Δ ₅ = 2*4,5 + 2*0 + 2*2,5 – 12 = 2 > 0, т.е. включение в план изделия «Д» ценой 12 ед. нецелесообразно [2].

 

Задание 2.

Решить графическим методом типовую задачу оптимизации. Осуществить проверку правильности решения с помощью средств MS Excel (надстройки Поиск решения).

2.4. На имеющихся у фермера 400 гектарах земли он планирует посеять кукурузу и сою. Сев и уборка кукурузы требует на каждый гектар 200 ден. ед. затрат, а сои – 100 ден. ед.  На покрытие расходов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. ден. ед.. Каждый гектар, засеянный кукурузой, принесет 30 центнеров, а каждый гектар, засеянный соей – 60 центнеров. Фермер заключил договор на продажу, по которому каждый центнер кукурузы принесет ему 3 ден. ед., а каждый центнер сои – 6 ден. ед. Однако, согласно этому договору, фермер обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. центнеров.

Фермеру хотелось бы знать, сколько гектар нужно засеять каждой из этих культур, чтобы получить максимальную прибыль.

Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум и почему?

Решение

Обозначим через х₁ сколько гектаров нужно засеять кукурузы, через х₂ – сои. Так как у фермера всего имеется 400 га земли, то первое ограничение задачи имеет вид:   х₁+ х₂ ≤ 400. Найдем общие затраты на сев и уборку кукурузы и сои: (200х₁+100х₂) ден. ед. Фермер получил на расходы ссуду в 60 тыс. ден., поэтому следующее ограничение имеет вид: 200х₁+100х₂ ≤ 60 000. Найдем, сколько центнеров зерна соберет фермер: (30х₁+60х₂) ц. Вместимость склада составляет 21 тыс. центнеров, поэтому следующее ограничение имеет вид: 30х₁+60х₂ ≤ 21 000. Выясним сколько ден. ед. получит фермер по договору за собранное зерно: (30х₁∙3+60х₂∙6) ден. ед.

Построим экономико-математическую модель задачи:

max F(X) = 90x₁+120x₂

х₁+ х₂ ≤ 400

200х₁+100х₂ ≤ 60 000

30х₁+60х₂ ≤ 21 000

x_1,2 ³ 0

Решим задачу графическим методом.

Последнее ограничение означает, что область решений будет лежать в первой четверти декартовой системы координат.

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

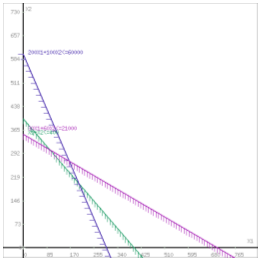
Рис. 1.

Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

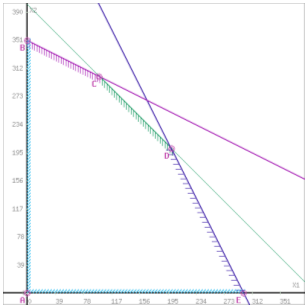
Рис. 2. Обозначим границы области многоугольника решений.

Рассмотрим целевую функцию задачи F = 90x₁+120x₂ → max.

Построим прямую, отвечающую значению функции F = 0:

F = 90x₁+120x₂ = 0.

Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (90; 120). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

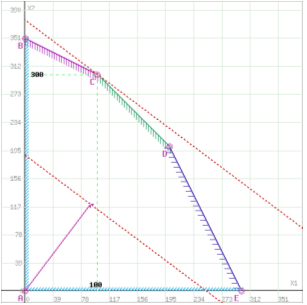
Рис. 3. Область допустимых решений представляет собой многоугольник

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения первой и третьей прямой, то ее координаты удовлетворяют уравнениям этих прямых:

x₁+x₂=400

30x₁+60x₂=21000

Решив систему уравнений, получим: x₁ = 100, x₂ = 300

Откуда найдем максимальное значение целевой функции:

F(X) = 90*100 + 120*300 = 45000

Если поставить задачу минимизации функции F(Х) = 90x₁+120x₂ при тех же ограничениях, линию уровня необходимо смещать параллельно самой себе в направлении, противоположном вектору-градиенту. В нашем случае минимум функции будет в точке A(0;0). Это означает, что фермер не получит ни чего, если не засеет поле зерновыми культурами.

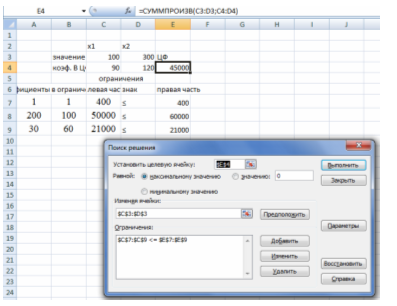
Проверим решение в Эксель [2].

 

Задание 3.

Рассчитать параметры моделей экономически выгодных размеров заказываемых партий.

3.4. Торговая компания собирается приобрести новый товар: комплекты постельного белья. Ожидаемая потребность - 800 единиц в месяц. Товар можно приобрести у поставщика, стоимость заказа – 150 руб., а годовая стоимость хранения – 6 руб. за единицу товара. Время необходимое для доставки товара составляет 2 дня. Компания работает 300 дней в году. Какой объем заказа минимизирует общие годовые расходы? Определите годовые расходы на хранение запасов, период поставок, точку заказа.

Решение

T=300 рабочих дней в году

λ=800*12=9600 компл./год

h=4 руб./компл. в год

s=150 руб./зак.

t=2 дн.

 

Задание 4.

Использовать методы теории массового обслуживания для исследования предлагаемой хозяйственной ситуации. При моделировании предполагается, что поток требований на обслуживание является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному (показательному) закону. Задачу следует решить с помощью средств MS Excel.

В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.), когда оба бухгалтера заняты обслуживанием ранее обратившихся работников, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно l; среднее время, которое затрачивает бухгалтер на оформление документа, равно Т_ср мин. (значения l и Т_ср по вариантам даны ниже в таблице).

Оценить основные характеристики работы данной бухгалтерии как СМО с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%?

№ варианта, задачи	Параметр l	Параметр Тср=1/μ
4.4	8	7

Решение

Рассчитаем вероятность отказа в обслуживании по формуле:

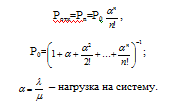
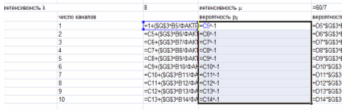
Рис. 1. Расчет вероятности Р_0.

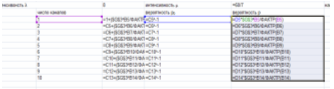
Рис. 2. Расчет вероятности отказа в обслуживании.

Относительная пропускная способность В, т.е. вероятность того, что заявка будет обслужена:

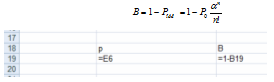
Рис. 3. Расчет вероятности обслуживания заявки.

Абсолютная пропускная способность А получим, умножая интенсивность потока заявок

---

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

---

Чтобы скачать бесплатно Контрольные работы на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Контрольные работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

---

Если Контрольная работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

---

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

---